the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
On the alignment of velocity and magnetic fields within magnetosheath jets
Ferdinand Plaschke
Maria Jernej
Heli Hietala
Laura Vuorinen
Jets in the subsolar magnetosheath are localized enhancements in dynamic pressure that are able to propagate all the way from the bow shock to the magnetopause. Due to their excess velocity with respect to their environment, they push slower ambient plasma out of their way, creating a vortical plasma motion in and around them. Simulations and case study results suggest that jets also modify the magnetic field in the magnetosheath on their passage, aligning it more with their velocity. Based on Magnetospheric Multiscale (MMS) jet observations and corresponding superposed epoch analyses of the angles ϕ between the velocity and magnetic fields, we can confirm that this suggestion is correct. However, while the alignment is more significant for faster than for slower jets, and for jets observed close to the bow shock, the overall effect is small: typically, reductions in ϕ of around 10∘ are observed at jet core regions, where the jets' velocities are largest. Furthermore, time series of ϕ pertaining to individual jets significantly deviate from the superposed epoch analysis results. They usually exhibit large variations over the entire range of ϕ: 0 to 90∘. This variability is commonly somewhat larger within jets than outside them, masking the systematic decrease in ϕ at core regions of individual jets.
- Article
(2804 KB) - Full-text XML
- BibTeX
- EndNote
The region downstream of the Earth's bow shock, the magnetosheath, is oftentimes permeated by localized plasma entities of significantly enhanced dynamic pressure, so-called magnetosheath jets (for a recent review, see Plaschke et al., 2018). Within those jets, the dynamic pressure can easily exceed values measured in the pristine solar wind, and a significant fraction of jets even feature super-magnetosonic plasma velocities (Savin et al., 2008, 2014; Hietala et al., 2009; Plaschke et al., 2013). Thus, jets are highly distinctive phenomena in the subsolar magnetosheath.
Jets are known to occur more often downstream of the quasi-parallel shock (Archer and Horbury, 2013; Plaschke et al., 2013, 2016). In the subsolar magnetosheath, their occurrence is, hence, enhanced when the interplanetary magnetic field (IMF) points in a quasi-radial direction, i.e., when the angle between the IMF and the Earth–Sun line – the IMF cone angle – is low. Under these conditions, shock-reflected particles are able to propagate along the IMF into the region upstream of the shock, where the particles then interact with the solar wind. The interaction region, called foreshock, exhibits localized magnetic-field and plasma structures (e.g., short large-amplitude magnetic structures; SLAMS) and waves that are convected back to the shock and which merge into it and thus continuously form and reform it (e.g., Schwartz and Burgess, 1991; Omidi et al., 2005; Blanco-Cano et al., 2006a, b). As a result, the quasi-parallel shock may be regarded as undulated or rippled. At the inclined surfaces of such ripples, solar-wind plasma may be less decelerated and heated, yet still compressed and focused, yielding coherent high-speed jets within slower ambient plasma in the downstream magnetosheath region (Hietala et al., 2009, 2012). As suggested by Karlsson et al. (2015, 2018) and shown in simulations by Palmroth et al. (2018), SLAMS themselves may become jets as they propagate through the undulated bow shock.
A second, smaller group of jets appears to be associated with the passage of IMF discontinuities, in particular when the character of the shock changes from quasi-perpendicular to quasi-parallel (Dmitriev and Suvorova, 2012; Savin et al., 2012; Archer et al., 2012; Plaschke et al., 2017). In this context, jets have also been associated with hot flow anomalies (HFAs) that can occur when an IMF discontinuity interacts with the bow shock (Schwartz et al., 2000; Omidi and Sibeck, 2007).
Jets link the processes in the foreshock and at the bow shock with effects at the magnetopause, in the magnetosphere, and on the ground. Upon impact on the magnetopause, jets are able to indent the boundary significantly (e.g., Shue et al., 2009; Amata et al., 2011), launching waves on the surface of the magnetopause and in the magnetosphere (Plaschke and Glassmeier, 2011; Archer et al., 2013a, b, 2019), and/or triggering magnetic reconnection (Hietala et al., 2018). Effects of the interaction are also visible from the ground as ionospheric flow enhancements, geomagnetic variations, or dayside auroral activity (Hietala et al., 2012; Dmitriev and Suvorova, 2012; Han et al., 2016, 2017; Wang et al., 2018). Jets are very common in the magnetosheath. In general, large-scale jets – larger than 2 Earth radii (RE) in diameter – hit the magnetopause approximately every 20 min. Under conditions of a low IMF cone angle, this rate increases to approximately one jet every 6 min (Plaschke et al., 2016). Note that typical observed jet scale sizes are on the order of 1 RE.
Recently, the inner structure of jets and their interaction with ambient magnetosheath plasma and fields have gotten more attention (Karimabadi et al., 2014; Plaschke et al., 2017; Plaschke and Hietala, 2018): when jets plow through slower ambient plasma, that latter plasma is pushed out of the way. Behind the jets, ambient plasma moves in to refill the wake. In addition, the fast motion of jets through slower ambient plasma may modify the magnetic field inside jets and in their vicinity, as seen in simulations by Karimabadi et al. (2014): the field may become more aligned with the plasma flow inside jets (see Fig. 1a). This hypothesis is supported by Plaschke et al. (2017), who found magnetic-field and velocity measurements to be correlated within 18 jets that occurred during a 1 h long interval. However, their case study could not yield conclusive evidence on how the magnetic field changes, on average, on the passage of a jet. The purpose of this paper is to obtain and present this information.
The results of this study are relevant in the context of solar-wind–magnetosphere coupling, as the magnetosheath plasma and fields represent the input to any interaction with the geomagnetic field at the magnetopause. Jet-induced changes in the magnetic field are expected to have repercussions on magnetosheath current sheets, on reconnection within the magnetosheath (Vörös et al., 2017), and at the magnetopause (Hietala et al., 2018), as well as on the associated triggering of substorms (Nykyri et al., 2019).
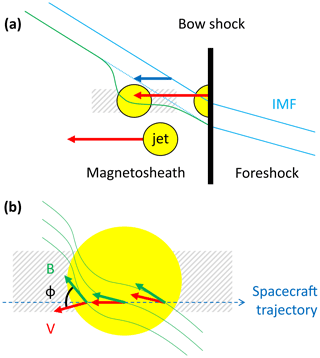
Figure 1(a) Sketch of how magnetic fields in the magnetosheath may be modified by the motion of fast plasma jets. Velocities of jets and ambient plasmas are illustrated by red and blue arrows, respectively. In this paper, magnetic and velocity fields within the hatched area are evaluated. This figure is based on Fig. 12 in Plaschke et al. (2017). (b) Close-up on a jet. Green and red arrows show local directions of the magnetic-field B and velocity V measured by a spacecraft on its trajectory through the jet. The angle between B and V is ϕB,V.
This study is based on jet observations by the four Magnetospheric Multiscale (MMS) spacecraft (Burch et al., 2016) made during the first and second dayside seasons of the mission (between 1 September 2015, the start of mission phase 1a, and 1 May 2017, the end of phase 2a). The MMS spacecraft were launched on 13 March 2015 into a highly elliptical and nearly equatorial orbit. The initial apogee distance of the spacecraft from Earth was 12 RE. This distance stayed the same in 2015 and 2016 and was raised in the first few months of 2017 to follow the dawn magnetopause as the orbit swept westwards. Consequently, the spacecraft spent significant time in the vicinity of the subsolar magnetopause, flying in close tetrahedral configuration with spacecraft separations between 60 and less than 10 km to achieve their primary goal: to investigate the small-scale physics of magnetic reconnection. While in the magnetosheath, they observed numerous jets.
To obtain a data set of jet observations by the MMS spacecraft, we follow the steps described in detail in Plaschke et al. (2013). We preselect intervals where the MMS spacecraft were located within a 30∘ wide cone centered at Earth and open to the Sun (∼ 10:00 to 14:00 in local time) at distances above 7 and below 18 RE from the Earth's center. Within those preselected intervals, magnetosheath intervals are identified by the ion density surpassing twice the density in the solar wind. Here, we use MMS ion density moments from the Fast Plasma Investigation (FPI; Pollock et al., 2016). These are compared to proton density measurements from NASA's OMNI high-resolution data set (King and Papitashvili, 2005), averaged over 5 min preceding any time of interest. Note that OMNI measurements are based on solar-wind monitor data from, e.g., the Advanced Composition Explorer (ACE) and Wind spacecraft, propagated to the bow shock nose. The 5 min averaging accounts for further propagation to the positions of the MMS spacecraft, closer to the magnetopause. In addition, within magnetosheath intervals the ion omnidirectional energy flux density of 1 keV ions (measured also by FPI) shall be larger than that of 10 keV ions, to exclude magnetospheric observations. The magnetosheath intervals shall be at least 2 min long and all quantities of interest shall be available, i.e., magnetic-field measurements by the MMS Fluxgate Magnetometers (FGM; Russell et al., 2016; Torbert et al., 2016), ion moments, and distribution functions by FPI and OMNI solar-wind magnetic-field and ion moments. Therewith, MMS 1 to 4 yield a total of 4345.5 h of magnetosheath data in 9375 intervals. Note that the intervals are almost equally distributed among the four MMS spacecraft, due to their close configuration: MMS 1, 2, 3, and 4 contribute 2376, 2370, 2279, and 2350 intervals, respectively.
Within these magnetosheath intervals, we search for jets as described in Plaschke et al. (2013). The main criterion is based on the dynamic pressure in the anti-sunward, i.e., x direction, in geocentric solar ecliptic (GSE) coordinates: . Here ρ is the ion (proton) mass density and Vx the velocity in the x direction. Pdyn,x – measured by MMS – shall surpass half the pristine-solar-wind value, as determined from OMNI solar-wind data (). A jet interval is then defined by . Intervals of 1 min before the start and after the end of the jet intervals are denoted as pre-jet and post-jet intervals. All pre-jet, jet, and post-jet intervals shall be within one magnetosheath interval as defined above.
The times of maximum ratio of dynamic pressures (magnetosheath over solar wind) are denoted as t0. We require Vx to be negative within jet intervals. should fall below half of its value at t0 within both pre- and post-jet intervals, as specified in Plaschke et al. (2013). Applying all those criteria, we obtain a data set of 9757 jets, where MMS 1, 2, 3, and 4 contribute 2460, 2466, 2354, and 2477 jets, respectively. Obviously, due to the small spacecraft separations, jets seen by one spacecraft are likely to be seen by the other three spacecraft as well.
Similar to Plaschke and Hietala (2018), we introduce normalized times : corresponds to the start of the pre-jet interval, is the start of the jet interval, tn=0 equals t0, i.e., the time of the maximum dynamic-pressure ratio in the jet core, tn=1 denotes the end of the jet interval, and tn=2 would be the end of the post-jet interval. Normalized times are defined for all 9757 jets. Note that normalized times correspond with times 0…4 in Plaschke and Hietala (2018).
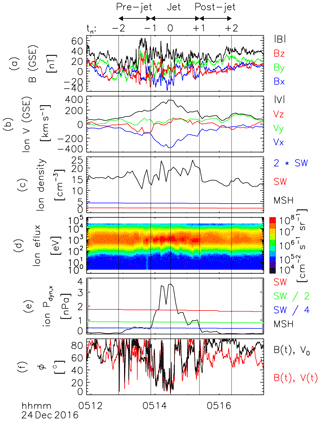
Figure 2Jet example: MMS 1 magnetosheath and OMNI solar-wind data of 24 December 2016. From top to bottom: (a) magnetic-field B in GSE; (b) ion velocity V in GSE; (c) ion density in the magnetosheath in black and (twice) the ion density in the solar wind in red (blue); (d) magnetosheath ion energy flux density; (e) Pdyn,x in the magnetosheath in black and in the solar wind in red (half and one quarter thereof in green and blue); and (f) angles in black and ϕB,V in red based on magnetosheath observations. Vertical lines show normalized times to 2.
Figure 2 shows one of these jets, exemplarily, observed by MMS 1 on 24 December 2016. As can be seen in Fig. 2c, the ion density clearly exceeded twice the corresponding solar-wind values, indicating the presence of MMS 1 in the magnetosheath. This is in agreement with Fig. 2d showing the ion omnidirectional energy flux density, also indicating that MMS 1 was immersed in thermalized magnetosheath plasma. Therein, the spacecraft observed a clear increase in GSE Vx (Fig. 2b), corresponding with a large increase in Pdyn,x (Fig. 2e), over the threshold of half the solar-wind dynamic pressure. The vertical lines in the figure indicate the normalized times to 2, at 05:12:52, 05:13:52, 05:14:29, 05:15:23, and 05:16:23 UT, respectively. We can use these normalized times to perform superposed epoch analyses, based on pre-jet, jet, and post-jet data; therefore, the respective time intervals are compressed/expanded to become equal between integer tn.
Note that time intervals between and −1 and between tn=1 and 2 are 1 min long by definition. The median lengths of time intervals between and 0 and between tn=0 and 1 are 20 s (lower and upper quartiles: 10 and 37 s) and 19 s (lower and upper quartiles: 10 and 39 s), respectively. Hence, in “real” time, the jet interval length can vary significantly, while typically being one third as long as the pre- and post-jet intervals combined (see also Plaschke et al., 2013).
Finally, we determine the relative locations rrel of jet-observing spacecraft at times tn=0 between the magnetopause (rrel=0) and the bow shock (rrel=1). Therefore, we use the magnetopause and bow shock models by Shue et al. (1998) and Merka et al. (2005), respectively (see Plaschke et al., 2013; Hietala and Plaschke, 2013). OMNI solar-wind data pertaining to jet times are the input conditions to the model calculations. There are 1856 jets observed closest to the magnetopause (rrel<0.25) and 797 jet observed closest to the bow shock (rrel>0.75). Hence, the vast majority of jets are associated with central locations within the subsolar magnetosheath.
The primary objective of this paper is to show whether (or not) the magnetic field aligns with the flow velocity on jet passage, as suggested by simulation results presented in Karimabadi et al. (2014) and case study observations by Plaschke et al. (2017). This can be answered by a superposed epoch analysis of the angle ϕB,V between magnetic-field B(t) and ion velocity V(t) vectors. The result is shown in red in Fig. 3 (see also the red line in Fig. 2f for a contributing example). The solid line shows median values, and the dashed lines illustrate the upper and lower quartiles. Note that the angles ϕ in all figures are acute angles, i.e., restricted between 0 and 90∘. We have checked that this does not limit the angular deflections resulting from the superposed epoch analyses.
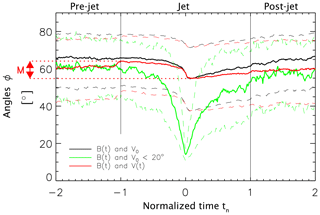
Figure 3Superposed epoch analyses of the angles ϕB,V in red, in black, and of those jets where that angle is limited to 20∘ at tn=0 in green. Solid lines show median values; dashed lines show upper- and lower-quartile values. Red dotted lines mark minimum and maximum values of median ϕB,V angles: the difference between these two values is ∘.
Let us focus first on the edges of the jet interval. Before and after that interval, in the pre- and post-jet intervals, the angle ϕB,V is approximately 60∘ and constant. At , a slight increase in the median and lower quartile of ϕB,V can be seen. This corresponds to the increase in dynamic pressure Pdyn,x over one quarter of the solar-wind value. At tn=1, the end of the jet interval, no significant feature in ϕB,V can be discerned. Instead, at that time, ϕB,V is gradually recovering from a decrease that sharply happens at tn=0.
The normalized time tn=0 (or t0) is of special importance, as it marks the time of maximum dynamic pressure in the jet, the jet core. Decreases in ϕB,V at that time show that, generally, there is “some” alignment of B and V happening inside jets. However, in the superposed epoch analysis, this effect is limited: the difference MB,V between the maximum and the minimum of the median angle ϕB,V is 9.4∘. MB,V is indicated by a red arrow in Fig. 3.
Angles can also be computed by using the velocity vector at that specific time (V0=V(t0)) and by comparing it with time series of magnetic-field vectors B(t). The direction of V0 should be a good indication of the overall jet propagation direction. Note that good deHoffmann–Teller frames exist for almost all jets and that the directions of V0 are generally consistent with the directions of the deHoffmann–Teller frame velocities, computed from V and B measurements between normalized times and 1 (Sonnerup et al., 1990).
Results of the superposed epoch analysis of are shown in black in Fig. 3 (see also the black line in Fig. 2f for a contributing example). In this case, the median shows no variation at . The decrease at tn=0 is a bit deeper (∘) because the overall value of within the pre- and post-jet intervals is slightly higher, approximately at 65∘.
The limited alignment effect apparent at tn=0 raises the question as to whether the considered effect is significant in any of the jets. Therefore, we select those jets where ∘ at tn=0. This holds for 449 jets, i.e., for 4.6 % of the jet data set. Note that the example jet shown in Fig. 2 belongs to this group. The corresponding superposed epoch analysis of based only on these jets is shown in green in Fig. 3. Apparently, a major alignment of B and V does happen sometimes, although only in a small minority of cases. For this subsample of jets, ∘ is obtained.
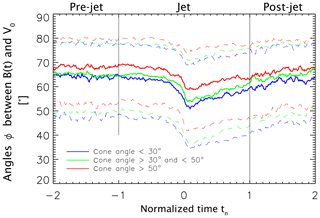
Figure 4Superposed epoch analyses of the angle using only jets occurring under IMF cone angles of (blue; 2811 contributing jets), between 30 and 50∘ (green; 4119 contributing jets), and above 50∘ (red; 2827 contributing jets), respectively. As in Fig. 3, solid lines show median values, and dashed lines show upper and lower quartiles.
The alignment effect may depend on the upstream solar-wind or jet-intrinsic conditions. As reported in Plaschke et al. (2013), the jet occurrence in the subsolar magnetosheath is heavily dependent on the IMF cone angle. The decrease in at t0, however, is only weakly dependent on this quantity, as can be seen in Fig. 4. In this figure, blue, green, and red solid lines correspond to the median angles of based on jets observed during conditions of a low, medium, and high IMF cone angle: <30, 30 to 50, and >50∘. Median cone angles associated with these categories are 20.9, 39.8, and 61.3∘. The corresponding alignment effect strengths of are 14.6, 13.9, and 10.5∘, respectively.
The overall levels also change slightly with the IMF cone angle, with B and V being a few degrees more aligned, in general, under conditions of a low IMF cone angle. The same results with respect to cone angle dependence holds for the angles of ϕB,V as a function of tn (not shown). Note that using IMF cone angle measurements 20 min before tn=0 instead of at tn=0 noticeably increases the alignment effect strength for events of a low cone angle to ∘.
The decrease in at t0 is more strongly dependent on the velocity of the jets (Fig. 5). The larger the velocity at t0 is, the larger the decrease will usually be in . Figure 5 shows superposed epoch analyses of this quantity as a function of V0x at t0. The blue, green, red, and black solid lines correspond to the median angles of based on jets featuring velocities , −200 to −150, −250 to −200, and km s−1. The median velocities V0x associated with these four categories are −130, −175, −221, and −293 km s−1. The corresponding alignment effect strengths of are in these cases 8.9, 11.3, 14.7, and 18.8∘, respectively. There is a clear linear dependency of on the median V0x values of the form ∘ − (0.0612∘ s km−1) V0x.
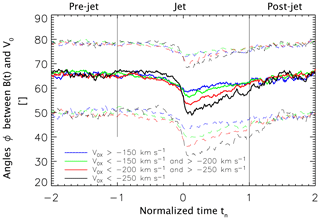
Figure 5Superposed epoch analyses of the angle using only jets featuring km s−1 in blue (1623 contributing jets), −150 km s−1 > km s−1 in green (3087 contributing jets), −200 km s−1 > km s−1 in red (2699 contributing jets), and −250 km s−1 > V0x in black (2348 contributing jets). As in Fig. 3, solid lines show median values and dashed lines show upper and lower quartiles.
Finally, we check the change in on jet passage as a function of the location of the observation between the magnetopause (rrel=0) and the bow shock (rrel=1). The results of the corresponding superposed epoch analyses are shown in Fig. 6. As can be seen, the green and red traces corresponding to mid-sheath jets () are almost identical to each other and also extremely similar to the black line in Fig. 3. There are, however, deviations in the alignment of the magnetic and velocity fields when it comes to jets observed closest to the magnetopause (rrel<0.25, blue line) and closest to the bow shock (rrel>0.25, black line). In the former case, ∘ is not dissimilar to the overall value of 12.1∘, but the alignment effect seems less concentrated around tn=0. In the latter case, the alignment effect is clearly stronger, and we obtain ∘.
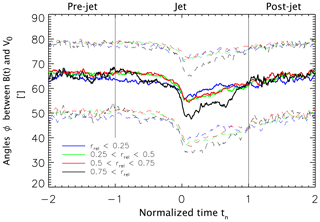
Figure 6Superposed epoch analyses of the angle as a function of the relative location of jet observations between the magnetopause (rrel=0) and the bow shock (rrel=1). As in Fig. 3, solid lines show median values and dashed lines show upper and lower quartiles.
It should be noted that the MMS spacecraft are more likely to observe the bow shock when the entire magnetospheric system is compressed, i.e., when the solar-wind dynamic pressure Pdyn,sw is high. In agreement therewith, the mean Pdyn,sw values pertaining to the four categories of rrel<0.25, between 0.25 and 0.5, between 0.5 and 0.75, and rrel>0.75 are , 2.22, 2.74, and 3.39 nPa, respectively. This raises the question as to whether the alignment effect is strongly dependent on the upstream dynamic pressure. The answer to this question is displayed in Fig. 7.
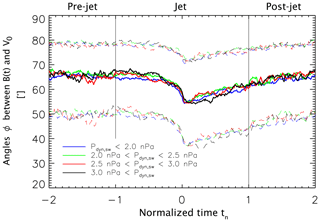
Figure 7Superposed epoch analyses of the angle as a function of the upstream solar-wind dynamic pressure Pdyn,sw. As in Fig. 3, solid lines show median values and dashed lines show upper and lower quartiles.
As can be seen in that figure, higher Pdyn,sw values are not associated with significant increases in alignment between B and V at tn=0. We have also tested the relation of other upstream solar-wind conditions (velocity, density, magnetic-field strength, and Mach numbers) to the time series of angles and ϕB,V. We have not found any indications of these conditions being related to larger systematic changes in alignment.
The typical angles between magnetic-field and plasma flow directions in the subsolar magnetosheath are reflected at normalized times and 2, at the ends of the superposed epoch analyses. As shown in Figs. 3 to 7, the median angles ϕB,V and at these times are found to be between approximately 60 and 70∘. At first glance, such high values seem remarkable, taking into account that they are also found under conditions of a low IMF cone angle (blue line in Fig. 4). However, they may be explained to a great extent by typical draping of the IMF in the magnetosheath. The median angle ϕB,V of all magnetosheath observations by the MMS spacecraft selected for this study is 59.2∘. This value corresponds quite well with median angles of ϕB,V at times and 2 (red solid line in Fig. 3). Note, however, that this angle is specific to the distribution of locations of the MMS spacecraft in the subsolar magnetosheath. Different locations, e.g., towards the flanks, will be associated with different typical angles of ϕB,V, which are a function of the combined draping and flow patterns.
The first jet-induced deviations in ϕB,V and are seen at . At this time, the median angle ϕB,V increases slightly, while does not change. As V0 stays constant, the change necessarily has to come from a change in V at . This change is reflected in Fig. 8, which shows superposed epoch analyses of the angles between V(t) with V0 and ex in black and red, respectively. Here, ex is the unit vector in the GSE x direction, along the Earth–Sun line.
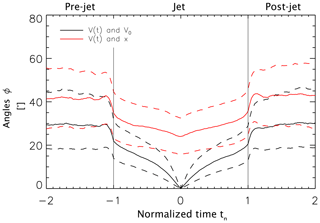
Figure 8Superposed epoch analysis of the angle between V(t), the time series of velocity vectors, and V0, the vectors at times t0 in black. In red, the superposed epoch analysis of is shown, where ex is the unit vector in GSE x direction.
As can be seen in the figure, between and 1 the jet-related plasma deflection takes place, with jets propagating more in the anti-sunward direction than the ambient magnetosheath plasma. This feature is typical for jets and has been reported, e.g., by Karlsson et al. (2012), Archer and Horbury (2013), and Plaschke et al. (2013). Apparently, the flow deflection does not affect the magnetic-field direction so that stays constant at . After that time, V gradually approaches V0, as reflected in Fig. 8 (see black line). Consequently, angles ϕB,V and behave rather similarly close to tn=0. This can also be seen in Fig. 2f, showing black and red lines closely aligned at tn=0 but deviating more strongly before and, in particular, after tn=1.
In light of the decreases of at tn=0, we can confirm that jets modify magnetic fields in the magnetosheath, tending to align them with their direction of propagation. This alignment happens sharply at tn=0, i.e., at the cores of the jets that feature the fastest plasma (see Plaschke and Hietala, 2018). However, it is also clear from the statistics presented in this paper that the alignment effect is generally small – much smaller than seen in simulations by Karimabadi et al. (2014). The reason for this discrepancy might be the restrictions imposed on plasma motion in their simulations, as they were 2-D and not 3-D.
In general, median angles decrease by approximately ∘. The statistics including only the fastest jets exhibit a decrease by approximately 20∘ and so do the statistics including only jets observed close to the bow shock (rrel>0.75). The fact that faster jets lead to a stronger alignment of B and V is not surprising, as the velocity difference between jets and ambient plasmas should be responsible for the change in magnetic-field direction (see Fig. 1a). As jets plow through slower plasma, they should drag the frozen-in magnetic field with them, straightening it at and after their passage (Plaschke et al., 2017). This picture is also in agreement with the gradual recovery of after the passage of the jet core, starting at tn=0 and extending beyond tn=1.
The fact that the alignment effect of B and V is stronger for jets observed close to the bow shock (the source region) is, however, somewhat puzzling. As a consequence, it can hardly be argued that the alignment effect increases as jets progress through the magnetosheath towards the magnetopause. Instead, the alignment may decrease as jets evolve. This may be due to the boundary conditions imposed by the magnetopause. The composition of jets observed close to the bow shock and the magnetopause may also be different. As reported in Plaschke et al. (2013), relatively more jets are observed close to the bow shock than close to the magnetopause. Hence, only a certain fraction of jets makes it all the way through the magnetosheath. It cannot be excluded that the alignment effect is generally smaller for that subset of jets.
A relatively large angular deviation of ∘ is also obtained for jets that were launched into a magnetosheath of that was preconditioned by a low IMF cone angle (cone angle <30∘ 20 min before tn=0). This result may suggest that the condition or state of the magnetosheath prior to jet generation may also have an influence on the alignment effect in particular and on jet evolution in general.
It shall be noted that all the results presented here pertain to changes in B and V emerging from superposed epoch analyses of thousands of jets. Individual jets can and will look very different. As shown in Fig. 3 in green, there are jets (<5 %) featuring a quite small ∘ at t0. The example jet shown in Fig. 2 is one of them. As can be seen in the bottom panel of Fig. 2, changes a lot over the passage of this particular jet, which is not special in this respect. Within its jet interval, between and tn=1, values close to 0 and 90∘ are reached in rapid succession.
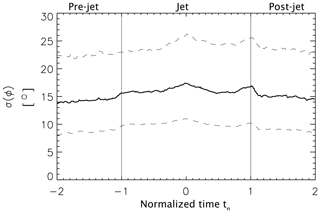
Figure 9Superposed epoch analysis of the inter-quartile range of angles ϕB,V within 10 s wide time intervals, centered around respective normalized times. Solid line depicts the median; dashed lines depict upper and lower quartiles.
To quantify this variability statistically, we compute the inter-quartile range σ of ϕB,V within 10 s wide sliding time intervals for every jet. The corresponding superposed epoch analysis of σ(ϕ) is presented in Fig. 9. Variability on the order of 14∘ seems to be typical. The median variability slightly increases within jet intervals to about 17∘ at tn=0. This increase is also suggested by the example displayed in Fig. 2. Note that the variability in ϕB,V is of the same order as the typical alignment at t0, quantitatively supporting the observation that the alignment is hard to discern in individual events.
The purpose of this paper is to ascertain whether the high-speed motion of magnetosheath jets through slower ambient plasma leads to an alignment of magnetic and velocity fields, as predicted by simulations (Karimabadi et al., 2014) and case study observations (Plaschke et al., 2017). To address this question, we have performed superposed epoch analyses of the angles ϕB,V and as a function of normalized times tn, based on MMS jet observations in the subsolar magnetosheath. These are our main results:
-
In agreement with expectations, jets generally do modify the magnetic field on their passage, aligning it more with their velocity. This alignment takes place at the core of the jets, at t0, and it is significantly stronger for faster jets and for jets observed close to the bow shock. Recovery to usual angles ϕ occurs gradually within the trailing part of the jets.
-
The alignment effect is not (strongly) dependent on the IMF cone angle, IMF strength, solar-wind velocity, density, dynamic pressure, or Mach numbers.
-
In disagreement with simulations by Karimabadi et al. (2014), this alignment is relatively small. Typically, the angles of ϕ change only by about 10∘. The reason for this discrepancy might be the restrictions imposed on plasma motion in the simulations, as they are 2-D and not 3-D.
-
Time series of ϕ of individual jets look very different to the superposed epoch analysis results: large fluctuations in ϕ on sub-jet time scales are very common. This variability is somewhat larger within jets than outside of them, masking the decrease in ϕ at times t0 of individual jets.
The FGM and FPI data used in this paper are stored at the MMS Science Data Center (https://lasp.colorado.edu/mms/sdc/, MMS, 2019) and are publicly available. The OMNI solar-wind data are publicly available from the NASA Space Physics Data Facility at the Goddard Space Flight Center (https://omniweb.gsfc.nasa.gov/ow_min.html, OMNI, 2019).
FP conceived the study, and MJ did a significant part of the data analysis work. HH and LV helped with the discussion and interpretation of the results.
The authors declare that they have no conflict of interest.
The dedication and expertise of the Magnetospheric Multiscale development and operations teams are greatly appreciated. We acknowledge the use of Level 2 fast-survey Fluxgate Magnetometer and Fast Plasma Investigation data. We acknowledge valuable discussions within the International Space Science Institute (ISSI) team called “Jets downstream of collisionless shocks” led by two authors of this paper (Ferdinand Plaschke and Heli Hietala).
The work at the University of Turku was supported by the Turku Collegium of Science and Medicine. The work of Heli Hietala was supported by the National Aeronautics and Space Administration (NASA; grant no. NNX17AI45G; contract no. NAS5-02099) and a Royal Society University Research Fellowship (no. URF\R1\180671).
This paper was edited by Matina Gkioulidou and reviewed by four anonymous referees.
Amata, E., Savin, S. P., Ambrosino, D., Bogdanova, Y. V., Marcucci, M. F., Romanov, S., and Skalsky, A.: High kinetic energy density jets in the Earth's magnetosheath: A case study, Planet. Space Sci., 59, 482–494, https://doi.org/10.1016/j.pss.2010.07.021, 2011. a
Archer, M. O. and Horbury, T. S.: Magnetosheath dynamic pressure enhancements: occurrence and typical properties, Ann. Geophys., 31, 319–331, https://doi.org/10.5194/angeo-31-319-2013, 2013. a, b
Archer, M. O., Horbury, T. S., and Eastwood, J. P.: Magnetosheath pressure pulses: Generation downstream of the bow shock from solar wind discontinuities, J. Geophys. Res., 117, A05228, https://doi.org/10.1029/2011JA017468, 2012. a
Archer, M. O., Hartinger, M. D., and Horbury, T. S.: Magnetospheric “magic” frequencies as magnetopause surface eigenmodes, Geophys. Res. Lett., 40, 5003–5008, https://doi.org/10.1002/grl.50979, 2013a. a
Archer, M. O., Horbury, T. S., Eastwood, J. P., Weygand, J. M., and Yeoman, T. K.: Magnetospheric response to magnetosheath pressure pulses: A low-pass filter effect, J. Geophys. Res., 118, 5454–5466, https://doi.org/10.1002/jgra.50519, 2013b. a
Archer, M. O., Hietala, H., Hartinger, M. D., Plaschke, F., and Angelopoulos, V.: Direct observations of a surface eigenmode of the dayside magnetopause, Nat. Commun., 10, 615, https://doi.org/10.1038/s41467-018-08134-5, 2019. a
Blanco-Cano, X., Omidi, N., and Russell, C. T.: Macrostructure of collisionless bow shocks: 2. ULF waves in the foreshock and magnetosheath, J. Geophys. Res., 111, A10205, https://doi.org/10.1029/2005JA011421, 2006a. a
Blanco-Cano, X., Omidi, N., and Russell, C. T.: ULF waves and their influence on bow shock and magnetosheath structures, Adv. Space Res., 37, 1522–1531, https://doi.org/10.1016/j.asr.2005.10.043, 2006b. a
Burch, J. L., Moore, T. E., Torbert, R. B., and Giles, B. L.: Magnetospheric Multiscale Overview and Science Objectives, Space Sci. Rev., 199, 5–21, https://doi.org/10.1007/s11214-015-0164-9, 2016. a
Dmitriev, A. V. and Suvorova, A. V.: Traveling magnetopause distortion related to a large-scale magnetosheath plasma jet: THEMIS and ground-based observations, J. Geophys. Res., 117, A08217, https://doi.org/10.1029/2011JA016861, 2012. a, b
Han, D.-S., Nishimura, Y., Lyons, L. R., Hu, H.-Q., and Yang, H.-G.: Throat aurora: The ionospheric signature of magnetosheath particles penetrating into the magnetosphere, Geophys. Res. Lett., 43, 1819–1827, https://doi.org/10.1002/2016GL068181, 2016. a
Han, D.-S., Hietala, H., Chen, X.-C., Nishimura, Y., Lyons, L. R., Liu, J.-J., Hu, H.-Q., and Yang, H.-G.: Observational properties of dayside throat aurora and implications on the possible generation mechanisms, J. Geophys. Res.-Space, 122, 1853–1870, https://doi.org/10.1002/2016JA023394, 2017. a
Hietala, H. and Plaschke, F.: On the generation of magnetosheath high-speed jets by bow shock ripples, J. Geophys. Res., 118, 7237–7245, https://doi.org/10.1002/2013JA019172, 2013. a
Hietala, H., Laitinen, T. V., Andréeová, K., Vainio, R., Vaivads, A., Palmroth, M., Pulkkinen, T. I., Koskinen, H. E. J., Lucek, E. A., and Rème, H.: Supermagnetosonic Jets behind a Collisionless Quasiparallel Shock, Phys. Rev. Lett., 103, 245001, https://doi.org/10.1103/PhysRevLett.103.245001, 2009. a, b
Hietala, H., Partamies, N., Laitinen, T. V., Clausen, L. B. N., Facskó, G., Vaivads, A., Koskinen, H. E. J., Dandouras, I., Rème, H., and Lucek, E. A.: Supermagnetosonic subsolar magnetosheath jets and their effects: from the solar wind to the ionospheric convection, Ann. Geophys., 30, 33–48, https://doi.org/10.5194/angeo-30-33-2012, 2012. a, b
Hietala, H., Phan, T. D., Angelopoulos, V., Oieroset, M., Archer, M. O., Karlsson, T., and Plaschke, F.: In Situ Observations of a Magnetosheath High-Speed Jet Triggering Magnetopause Reconnection, Geophys. Res. Lett., 45, 1732–1740, https://doi.org/10.1002/2017GL076525, 2018. a, b
Karimabadi, H., Roytershteyn, V., Vu, H., Omelchenko, Y., Scudder, J., Daughton, W., Dimmock, A., Nykyri, K., Wan, M., Sibeck, D., Tatineni, M., Majumdar, A., Loring, B., and Geveci, B.: The link between shocks, turbulence, and magnetic reconnection in collisionless plasmas, Phys. Plasmas, 21, 062308, https://doi.org/10.1063/1.4882875, 2014. a, b, c, d, e, f
Karlsson, T., Brenning, N., Nilsson, H., Trotignon, J.-G., Vallières, X., and Facsko, G.: Localized density enhancements in the magnetosheath: Three-dimensional morphology and possible importance for impulsive penetration, J. Geophys. Res., 117, A03227, https://doi.org/10.1029/2011JA017059, 2012. a
Karlsson, T., Kullen, A., Liljeblad, E., Brenning, N., Nilsson, H., Gunell, H., and Hamrin, M.: On the origin of magnetosheath plasmoids and their relation to magnetosheath jets, J. Geophys. Res., 120, 7390–7403, https://doi.org/10.1002/2015JA021487, 2015. a
Karlsson, T., Plaschke, F., Hietala, H., Archer, M., Blanco-Cano, X., Kajdič, P., Lindqvist, P.-A., Marklund, G., and Gershman, D. J.: Investigating the anatomy of magnetosheath jets – MMS observations, Ann. Geophys., 36, 655–677, https://doi.org/10.5194/angeo-36-655-2018, 2018. a
King, J. H. and Papitashvili, N. E.: Solar wind spatial scales in and comparisons of hourly Wind and ACE plasma and magnetic field data, J. Geophys. Res., 110, A02104, https://doi.org/10.1029/2004JA010649, 2005. a
Merka, J., Szabo, A., Slavin, J. A., and Peredo, M.: Three-dimensional position and shape of the bow shock and their variation with upstream Mach numbers and interplanetary magnetic field orientation, J. Geophys. Res., 110, A04202, https://doi.org/10.1029/2004JA010944, 2005. a
MMS: MMS mission data including FGM and FPI data, available at: https://lasp.colorado.edu/mms/sdc/public, last access: 13 March 2019. a
Nykyri, K., Bengtson, M., Angelopoulos, V., Nishimura, Y., and Wing, S.: Can Enhanced Flux Loading by High-Speed Jets Lead to a Substorm? Multipoint Detection of the Christmas Day Substorm Onset at 08:17 UT, 2015, J. Geophys. Res., 124, 4314–4340, https://doi.org/10.1029/2018JA026357, 2019. a
Omidi, N. and Sibeck, D. G.: Formation of hot flow anomalies and solitary shocks, J. Geophys. Res., 112, A01203, https://doi.org/10.1029/2006JA011663, 2007. a
Omidi, N., Blanco-Cano, X., and Russell, C. T.: Macrostructure of collisionless bow shocks: 1. Scale lengths, J. Geophys. Res., 110, A12212, https://doi.org/10.1029/2005JA011169, 2005. a
OMNI: NASA OMNI solar-wind data, available at: https://omniweb.gsfc.nasa.gov/ow_min.html, last access: 13 March 2019. a
Palmroth, M., Hietala, H., Plaschke, F., Archer, M., Karlsson, T., Blanco-Cano, X., Sibeck, D., Kajdič, P., Ganse, U., Pfau-Kempf, Y., Battarbee, M., and Turc, L.: Magnetosheath jet properties and evolution as determined by a global hybrid-Vlasov simulation, Ann. Geophys., 36, 1171–1182, https://doi.org/10.5194/angeo-36-1171-2018, 2018. a
Plaschke, F. and Glassmeier, K.-H.: Properties of standing Kruskal-Schwarzschild-modes at the magnetopause, Ann. Geophys., 29, 1793–1807, https://doi.org/10.5194/angeo-29-1793-2011, 2011. a
Plaschke, F. and Hietala, H.: Plasma flow patterns in and around magnetosheath jets, Ann. Geophys., 36, 695–703, https://doi.org/10.5194/angeo-36-695-2018, 2018. a, b, c, d
Plaschke, F., Hietala, H., and Angelopoulos, V.: Anti-sunward high-speed jets in the subsolar magnetosheath, Ann. Geophys., 31, 1877–1889, https://doi.org/10.5194/angeo-31-1877-2013, 2013. a, b, c, d, e, f, g, h, i, j
Plaschke, F., Hietala, H., Angelopoulos, V., and Nakamura, R.: Geoeffective jets impacting the magnetopause are very common, J. Geophys. Res., 121, 3240–3253, https://doi.org/10.1002/2016JA022534, 2016. a, b
Plaschke, F., Karlsson, T., Hietala, H., Archer, M., Vörös, Z., Nakamura, R., Magnes, W., Baumjohann, W., Torbert, R. B., Russell, C. T., and Giles, B. L.: Magnetosheath High-Speed Jets: Internal Structure and Interaction With Ambient Plasma, J. Geophys. Res., 122, 10157–10175, https://doi.org/10.1002/2017JA024471, 2017. a, b, c, d, e, f, g
Plaschke, F., Hietala, H., Archer, M., Blanco-Cano, X., Kajdič, P., Karlsson, T., Lee, S. H., Omidi, N., Palmroth, M., Roytershteyn, V., Schmid, D., Sergeev, V., and Sibeck, D.: Jets Downstream of Collisionless Shocks, Space Sci. Rev., 214, 81, https://doi.org/10.1007/s11214-018-0516-3, 2018. a
Pollock, C., Moore, T., Jacques, A., Burch, J., Gliese, U., Saito, Y., Omoto, T., Avanov, L., Barrie, A., Coffey, V., Dorelli, J., Gershman, D., Giles, B., Rosnack, T., Salo, C., Yokota, S., Adrian, M., Aoustin, C., Auletti, C., Aung, S., Bigio, V., Cao, N., Chandler, M., Chornay, D., Christian, K., Clark, G., Collinson, G., Corris, T., De Los Santos, A., Devlin, R., Diaz, T., Dickerson, T., Dickson, C., Diekmann, A., Diggs, F., Duncan, C., Figueroa-Vinas, A., Firman, C., Freeman, M., Galassi, N., Garcia, K., Goodhart, G., Guererro, D., Hageman, J., Hanley, J., Hemminger, E., Holland, M., Hutchins, M., James, T., Jones, W., Kreisler, S., Kujawski, J., Lavu, V., Lobell, J., LeCompte, E., Lukemire, A., MacDonald, E., Mariano, A., Mukai, T., Narayanan, K., Nguyan, Q., Onizuka, M., Paterson, W., Persyn, S., Piepgrass, B., Cheney, F., Rager, A., Raghuram, T., Ramil, A., Reichenthal, L., Rodriguez, H., Rouzaud, J., Rucker, A., Saito, Y., Samara, M., Sauvaud, J.-A., Schuster, D., Shappirio, M., Shelton, K., Sher, D., Smith, D., Smith, K., Smith, S., Steinfeld, D., Szymkiewicz, R., Tanimoto, K., Taylor, J., Tucker, C., Tull, K., Uhl, A., Vloet, J., Walpole, P., Weidner, S., White, D., Winkert, G., Yeh, P.-S., and Zeuch, M.: Fast Plasma Investigation for Magnetospheric Multiscale, Space Sci. Rev., 199, 331–406, https://doi.org/10.1007/s11214-016-0245-4, 2016. a
Russell, C. T., Anderson, B. J., Baumjohann, W., Bromund, K. R., Dearborn, D., Fischer, D., Le, G., Leinweber, H. K., Leneman, D., Magnes, W., Means, J. D., Moldwin, M. B., Nakamura, R., Pierce, D., Plaschke, F., Rowe, K. M., Slavin, J. A., Strangeway, R. J., Torbert, R., Hagen, C., Jernej, I., Valavanoglou, A., and Richter, I.: The Magnetospheric Multiscale Magnetometers, Space Sci. Rev., 199, 189–256, https://doi.org/10.1007/s11214-014-0057-3, 2016. a
Savin, S., Amata, E., Zelenyi, L., Budaev, V., Consolini, G., Treumann, R., Lucek, E., Safrankova, J., Nemecek, Z., Khotyaintsev, Y., Andre, M., Buechner, J., Alleyne, H., Song, P., Blecki, J., Rauch, J. L., Romanov, S., Klimov, S., and Skalsky, A.: High energy jets in the Earth's magnetosheath: Implications for plasma dynamics and anomalous transport, J. Exp. Theor. Phys. Lett., 87, 593–599, https://doi.org/10.1134/S0021364008110015, 2008. a
Savin, S., Amata, E., Zelenyi, L., Lutsenko, V., Safrankova, J., Nemecek, Z., Borodkova, N., Buechner, J., Daly, P. W., Kronberg, E. A., Blecki, J., Budaev, V., Kozak, L., Skalsky, A., and Lezhen, L.: Super fast plasma streams as drivers of transient and anomalous magnetospheric dynamics, Ann. Geophys., 30, 1–7, https://doi.org/10.5194/angeo-30-1-2012, 2012. a
Savin, S., Amata, E., Budaev, V., Zelenyi, L., Kronberg, E. A., Buechner, J., Safrankova, J., Nemecek, Z., Blecki, J., Kozak, L., Klimov, S., Skalsky, A., and Lezhen, L.: On nonlinear cascades and resonances in the outer magnetosphere, J. Exp. Theor. Phys. Lett., 99, 16–21, https://doi.org/10.1134/S002136401401010X, 2014. a
Schwartz, S. J. and Burgess, D.: Quasi-parallel shocks – A patchwork of three-dimensional structures, Geophys. Res. Lett., 18, 373–376, https://doi.org/10.1029/91GL00138, 1991. a
Schwartz, S. J., Paschmann, G., Sckopke, N., Bauer, T. M., Dunlop, M., Fazakerley, A. N., and Thomsen, M. F.: Conditions for the formation of hot flow anomalies at Earth's bow shock, J. Geophys. Res., 105, 12639–12650, https://doi.org/10.1029/1999JA000320, 2000. a
Shue, J. H., Song, P., Russell, C. T., Steinberg, J. T., Chao, J. K., Zastenker, G., Vaisberg, O. L., Kokubun, S., Singer, H. J., Detman, T. R., and Kawano, H.: Magnetopause location under extreme solar wind conditions, J. Geophys. Res., 103, 17691–17700, https://doi.org/10.1029/98JA01103, 1998. a
Shue, J.-H., Chao, J.-K., Song, P., McFadden, J. P., Suvorova, A., Angelopoulos, V., Glassmeier, K. H., and Plaschke, F.: Anomalous magnetosheath flows and distorted subsolar magnetopause for radial interplanetary magnetic fields, Geophys. Res. Lett., 36, L18112, https://doi.org/10.1029/2009GL039842, 2009. a
Sonnerup, B. U. O., Papamastorakis, I., Paschmann, G., and Luehr, H.: The magnetopause for large magnetic shear: Analysis of convection electric fields from AMPTE/IRM, J. Geophys. Res., 95, 10541–10557, https://doi.org/10.1029/JA095iA07p10541, 1990. a
Torbert, R. B., Russell, C. T., Magnes, W., Ergun, R. E., Lindqvist, P.-A., Le Contel, O., Vaith, H., Macri, J., Myers, S., Rau, D., Needell, J., King, B., Granoff, M., Chutter, M., Dors, I., Olsson, G., Khotyaintsev, Y. V., Eriksson, A., Kletzing, C. A., Bounds, S., Anderson, B., Baumjohann, W., Steller, M., Bromund, K., Le, G., Nakamura, R., Strangeway, R. J., Leinweber, H. K., Tucker, S., Westfall, J., Fischer, D., Plaschke, F., Porter, J., and Lappalainen, K.: The FIELDS Instrument Suite on MMS: Scientific Objectives, Measurements, and Data Products, Space Sci. Rev., 199, 105–135, https://doi.org/10.1007/s11214-014-0109-8, 2016. a
Vörös, Z., Yordanova, E., Varsani, A., Genestreti, K. J., Khotyaintsev, Y. V., Li, W., Graham, D. B., Norgren, C., Nakamura, R., Narita, Y., Plaschke, F., Magnes, W., Baumjohann, W., Fischer, D., Vaivads, A., Eriksson, E., Lindqvist, P.-A., Marklund, G., Ergun, R. E., Leitner, M., Leubner, M. P., Strangeway, R. J., Le Contel, O., Pollock, C., Giles, B. J., Torbert, R. B., Burch, J. L., Avanov, L. A., Dorelli, J. C., Gershman, D. J., Paterson, W. R., Lavraud, B., and Saito, Y.: MMS Observation of Magnetic Reconnection in the Turbulent Magnetosheath, J. Geophys. Res., 122, 11442–11467, https://doi.org/10.1002/2017JA024535, 2017. a
Wang, B., Nishimura, Y., Hietala, H., Lyons, L., Angelopoulos, V., Plaschke, F., Ebihara, Y., and Weatherwax, A.: Impacts of Magnetosheath High-Speed Jets on the Magnetosphere and Ionosphere Measured by Optical Imaging and Satellite Observations, J. Geophys. Res., 123, 4879–4894, https://doi.org/10.1029/2017JA024954, 2018. a





