the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Overshoot dependence on the cross-shock potential
Michael Gedalin
Xiaoyan Zhou
Christopher T. Russell
Vassilis Angelopoulos
Coherent downstream oscillations of the magnetic field in shocks are produced due to the coherent ion gyration and quasiperiodic variations of the ion pressure. The amplitude and the positions of the pressure maxima and minima depend on the cross-shock potential and upstream ion temperature. Two critical cross-shock potentials are defined: the critical gyration potential (CGP), which separates the cases of increase or decrease in the component of the velocity of the distribution center along the shock normal, and the critical reflection potential (CRP), above which ion reflection becomes significant. In a weak, very low upstream kinetic-to-magnetic pressure ratio, β, the shocks' CRP exceeds the CGP. For potentials below the CGP, the first downstream maximum of the magnetic field is shifted farther downstream and is larger than the second maximum. For higher potentials, the first maximum occurs just behind the ramp and is lower than the second maximum. With the increase in the upstream temperature, the CGP exceeds the CRP. For potentials below the CRP, the effects of ion reflection are negligible and the shock profile is similar to that of very low-β shocks. If the potential exceeds the CRP, ion reflection is significant, the magnetic field increase toward the overshoot becomes steeper, and the largest peak occurs at the downstream edge of the ramp.
Collisionless shocks (CSs) are one of the most efficient accelerators of charged particles in the universe. They are present in virtually all plasma environments at scales from ∼1 cm in the terrestrial labs to ∼1 Mpc in galaxy clusters. A CS is a multi-scale object, where the highest energies are achieved at the largest scales within the diffusive process due to scattering at fluctuations far upstream and far downstream and multiple crossings of the shock. The latter occur within the scatter-free region; thus, ion dynamics in the shock front is intimately related to the large-scale acceleration: while the diffusive acceleration occurs at scales much larger than the shock width, the spectrum of the accelerated particles is essentially determined by conservation laws at the scatter-free shock transition. The fields in the shock front are responsible for ion heating, generation of backstreaming ion beams (Burgess, 1987; Kucharek et al., 2004; Oka et al., 2005; Gedalin et al., 2008; Gedalin, 2016b), acceleration of pickup ions (Lee et al., 1996; Zank et al., 1996; Zilbersher and Gedalin, 1997; Ariad and Gedalin, 2013), and injection into the diffusive mechanism (Scholer et al., 2002; Giacalone, 2005). Thus, the structure of the shock front is the central problem of the shock physics. The shock structure can be studied with in situ measurements only at heliospheric shocks. Qualitative understanding of the shock structure has substantially improved due to these high quality observations and also due to numerical simulations. The frontier of observational shock studies has recently shifted towards the processes occurring within a few ion convective gyroradii in both directions from the ramp along the shock normal (Dimmock et al., 2012; Wilson et al., 2012, 2014; Johlander et al., 2016; Burgess et al., 2016; Eselevich et al., 2017; Wilson III et al., 2017; Gingell et al., 2017).
Magnetic profiles of collisionless shocks are rarely monotonic, even for low-Mach numbers (Greenstadt et al., 1975; Greenstadt et al., 1980; Russell et al., 1982a; Mellott and Greenstadt, 1984; Farris et al., 1993; Balikhin et al., 2008; Russell et al., 2009; Kajdič et al., 2012). As the peak value of the downstream oscillations increases with the increase in the Mach number, for a long time it was believed that overshoots were produced by ion reflection in super-critical shocks (Livesey et al., 1982; Russell et al., 1982b; Sckopke et al., 1983; Scudder et al., 1986; Mellott and Livesey, 1987). Super-critical shocks are the shocks with the Mach number exceeding the critical Mach number (Edmiston and Kennel, 1984; Kennel, 1987); thus, the resistivity (Edmiston and Kennel, 1984) and thermal conductivity (Kennel, 1987) alone cannot provide necessary dissipation to sustain a shock. Eventually coherent downstream oscillations were observed at a very low-Mach number shock (Balikhin et al., 2008) with the Alfvenic Mach number of M=1.3 and magnetic compression of . The oscillating trail behind the ramp exhibited all of the features expected for a supercritical shocks, such as the largest first peak, spatially periodical peaks, and the gradual decrease in the peak amplitude. Such oscillations, albeit often less ordered, were found to be common in low-Mach number shocks (Russell et al., 2009; Kajdič et al., 2012). They were successfully explained as a result of coherent ion gyration upon crossing the shock ramp and subsequent collisionless relaxation due to gyrophase mixing (Balikhin et al., 2008; Ofman et al., 2009; Ofman and Gedalin, 2013; Gedalin, 2015; Gedalin et al., 2015, 2018). It has been shown that the largest peak amplitude is mainly determined by the magnetic compression and cross-shock potential, whereas the damping rate of the oscillations is related to the upstream thermal-to-fluid speed ratio (Gedalin, 2015). Shapes of the downstream profile, like relative peaks of the first oscillations and steepness of the magnetic field increase up to the first peak, and vary considerably among observed shocks, even subcritical shocks. Thus far, sufficient attention has not been devoted to the relation of the details of the magnetic oscillation pattern to the shock parameters and ion kinetics in the shock front. In particular, amplitudes and positions of the first peaks, which are not yet distorted by gyrophase mixing, may provide information about the cross-shock potential as well about the ion transmission and reflection.
In what follows, Bu is the upstream magnetic field magnitude, Tu is the upstream ion temperature, nu is the upstream ion number density, is the upstream ion thermal speed, m is the ion mass, and is the upstream kinetic-to-magnetic pressure ratio. The corresponding parameters for electrons are denoted by adding index e. In order to explain the basic mechanism of producing the downstream oscillations, let us consider a simplified model of a perpendicular shock. We treat the shock as a jump in the magnetic field from Bu to Bd=RBu occurring within a narrow ramp. Accordingly, the fluid drift speeds upstream and downstream are Vu and , respectively. We shall also neglect the electron contribution in the plasma pressure and treat ions as a monoenergetic beam entering the shock with the velocity Vu along the shock normal. The analysis is carried out in the normal incidence frame, where x is along the shock normal (in the downstream direction) and z is along the magnetic field. The equations of motion for ions inside the ramp are
We integrate the equations of motion across the ramp assuming , where vT is the thermal speed of upstream ions. In this approximation we get
Here u denotes the ion velocity at the downstream edge of the ramp, whereas v(x) denotes the ion velocity at the position x inside the ramp. The second term in Eq. (3) is a small correction for ramp width ≲(c∕ωpi) and . Here (c∕ωpi) is the ion inertial length. This small correction can be neglected for our purposes. In Eq. (4) the only term is small but nonzero. Thus, if the cross-shock potential is , the ion velocity just after crossing the jump is
The ion motion is then described as a drift along the shock normal with the velocity Vu∕R and gyration around the magnetic field:
where is the downstream ion gyrofrequency. For a cold beam, all ions move together and the coordinate along the shock normal is given by
In general, it is not possible to derive an analytical expression for vx(x). For our purposes it is sufficient to restrict ourselves to weak gyration, , so that and x(t) is invertible; thus, t(x) is a single-valued function. Let us define the critical gyration potential (CGP) . For s<scr, the initial gyrophase φ≈0, so that at the downstream edge of the ramp. For s>scr, the initial gyrophase is φ≈π, so that at the downstream edge of the ramp.
The total (dynamic and kinetic) ion pressure is given by
where we have used the mass conservation nvx=nuVu. Pressure balance requires , so that the magnetic field has maxima at the minima of the ion pressure. The latter occur at the minima of vx. For s<scr, the velocity decreases inside the ramp and keeps decreasing down to at which approximately corresponds to for φ≈0. Thus, the first maximum of the magnetic field occurs at xl at the pressure . With the increase in s, the relative contribution of uy in v⟂ increases which moves the position of the first pressure minimum closer to the ramp. For s>scr, the velocity decreases inside the ramp but starts to increase just behind it. Thus, the first maximum of the magnetic field occurs at x=0 (the downstream edge of the ramp) at the pressure . As , one has ph>pl which means that the first peak will be lower than the subsequent peaks corresponding to the pressure minima pl.
For a cold ion beam the amplitude of further pressure oscillations does not change. Finite temperature leads to the divergence of the ion trajectories and gradual gyrophase mixing. The divergence already occurs at the shock crossing, as the downstream ion velocity , and the spread in vx,u results in a more substantial spread in vx,d. Moreover, there is nonzero vy that affects the gyration speed v⟂ and φ, which are now different for different particles:
The downstream ion pressure including finite temperature is obtained as an integral over the distribution
It has been shown (Gedalin et al., 2015; Gedalin, 2016a) that finite temperature results in collisionless relaxation during which the downstream ion distribution gyrotropizes and the pressure oscillations damp out. The relaxation is faster for larger vT∕Vu. In oblique shocks the mechanism of the generation of downstream oscillations is the same. Relaxation is faster for lower angles θ between the shock normal and the upstream magnetic field (Gedalin, 2015; Gedalin et al., 2015).
With the increase in the magnetic compression, the CGP rapidly increases. At R=2 this critical value is scr=0.75. Although such high cross-shock potentials cannot be completely excluded, they are not observed often (Dimmock et al., 2012). Thus, we expect that in most shocks the potential is below the CGP. Yet, in many shocks the first magnetic peak occurs right at the downstream edge of the ramp. In many cases, it is also the largest peak. The above analysis is only valid, strictly speaking, for sufficiently low- shocks, as the number of quasi-reflected and/or reflected ions rapidly increases with the increase in vT∕Vu, where is the upstream thermal speed of ions (Gedalin, 2016b). In the narrow shock approximation, all ions that initially have cannot cross the ramp. This mode of reflection is efficient when . Deceleration of quasi-reflected ions inside the ramp can be expected to result in the faster reduction of the ion pressure with the distance from the upstream edge of the ramp – that is, a steeper increase in the magnetic field.
2.1 Advanced test-particle analysis vs. observations
The principles of the advanced test-particle analysis have been described in detail by Gedalin and Dröge (2013). In brief, a model magnetic field profile is chosen, supplemented by a model electric field shape. The basic upstream plasma parameters – that is ion and electron β and the angle between the shock normal and the upstream magnetic field θ – are chosen and remain fixed during the analysis. After choosing a magnetic compression ratio R, the rest of the significant parameters are varied. With each set of the parameters, ions are numerically traced across the shock, the ion pressure is determined, and the corresponding magnetic field is derived from the pressure balance. The parameters are varied until reasonable agreement is achieved with the adopted model profile: the asymptotic values of the magnetic field should be equal and the fluctuations should be as small as possible. It has been found that the most influential parameters are the Alfvenic Mach number M and the normalized cross-shock potential s . There is also weak dependence on the shock width D. The magnetic profile chosen for the analysis is taken in the following form:
with Bx=Bucos θ, , and . The coefficients of proportionality are constrained by the chosen values of the normal incidence frame (NIF) cross-shock potential sNIF and the de Hoffman–Teller potential sHT (Goodrich and Scudder, 1984; Scudder et al., 1986; Schwartz et al., 1988). The latter was found to almost not affect the ion motion and was kept at sHT=0.1 in the subsequent analysis. The post-tracing magnetic field was derived from the condition
where the ion pressure was determined numerically and for the electron pressure the polytropic equation of state was used, as well as the quasi-neutrality.
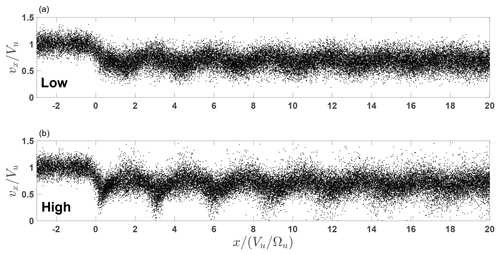
Figure 1 shows the results of the numerical analysis for both high (Fig. 1a) and low (Fig. 1b) potentials.
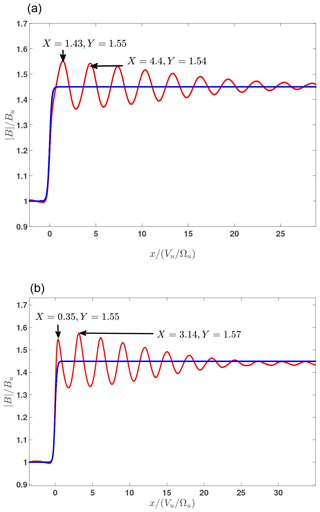
Figure 1Comparison of the derived magnetic profiles (red) for sNIF=0.4 (a) and sNIF=0.65 (b). In both cases R=1.45, M=1.4, and . The model magnetic field is shown by the blue line.
In both cases the magnetic compression R=1.45, the Alfvenic Mach number M=1.4, the shock angle , the upstream , and the width are the same. The CGP is in this case. It appears that the chosen shock parameters allow two different cross-shock potential values. The positions of the first two peaks and their values are shown for convenience. The coordinate is measured in . It is clearly seen that for the low potential the first peak is shifted farther downstream from the ramp and its amplitude is higher than that of the second peak. In the case of the higher potential the first peak occurs at the downstream edge of the ramp and its amplitude is lower than that of the second peak. Figure 2 illustrates the difference in the behavior of the normal component of the ion velocity, vx, in both cases. In the low-potential case this component continues to decrease well beyond the ramp. Subsequent dips become more and more shallow with distance from the ramp. In the high-potential case vx starts to increase upon crossing the ramp. The second dip is deeper because lower vx values are achieved, as explained above.
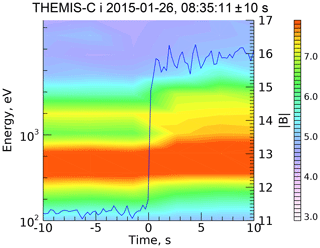
Parameters of the above analysis have been chosen close to those for two THEMIS-C crossings of the Earth bow shock, 30 March 2011, 08:09:40 UT and 30 March 2011, 08:51:40 UT (Pope et al., 2019). The magnetic profiles for these crossings are shown in Fig. 3 along with the ion spectrogram.
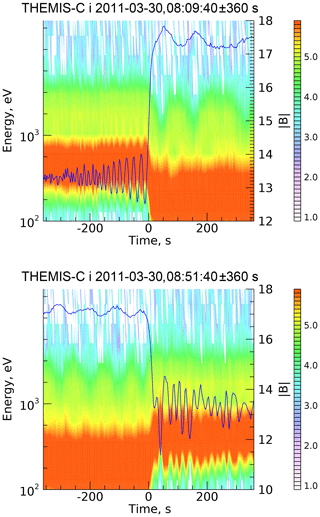
Figure 3Earth bow shock crossings by THEMIS-C on 30 March 2011. Magnetic profiles (magnitude) and ion spectrograms are plotted together.
The anticorrelation of the magnetic magnitude and the downstream ion pressure (greenish areas) are seen quite clearly at both shocks. Cross-shock potentials were calculated directly from observations (Pope et al., 2019) and found to be s=0.36 (for the shock in the top panel of Fig. 3) and s=0.50 (for the shock in the bottom panel of Fig. 3). The CGP is ccr≈0.4 for both shocks. Thus, the magnetic field profile of the shock in Fig. 3 (top panel) can be expected to be similar to that in Fig. 1a, whereas the bottom panel of Fig. 3 observed shock should be similar to the Fig. 1b model shock. Indeed, the positions and relative amplitudes of the first magnetic peaks in the observed shocks are in excellent agreement with the theoretical predictions.
With the increase in the magnetic compression, the CGP rapidly increases. For the CGP is rather high: ccr=0.75. In most shocks the cross-shock potential is expected to be below this value (Dimmock et al., 2012). In low-βi plasmas all ions are directly transmitted across the shock without reflection, and the above findings can be summarized as follows: (a) below the CGP the first peak is the strongest, (b) with the increase in the potential toward the CGP the first peak moves closer to the ramp, (c) upon crossing the CGP the first peak is located at the downstream edge of the ramp and is no longer the strongest.
Ion reflection occurs in supercritical and marginally critical shocks. Ion reflection is a kinetic process and the fate of an ion entering a shock front depends on the initial velocity of the ion. There are two major modes of ion reflection: post-ramp and in-ramp reflection. Post-ramp reflection occurs when an ion crosses the ramp, gyrates behind it, and returns back to the ramp to cross it in the upstream direction, but turns around again inside the ramp moving in the downstream direction. In-ramp reflection occurs when an ion changes its direction of motion inside the ramp and starts moving in the upstream direction. In both modes reflection occurs due to the combined effects of the electric and magnetic forces. As the transition from upstream to ramp and further downstream is continuous, there is no strict separation between the two modes. Efficiency of the post-ramp reflection increases most strongly with the increase in the magnetic compression Bd∕Bu. It also increases with the increase of the ratio and with the decrease in the cross-shock potential s (Gedalin, 1996). The inverse dependence on the cross-shock potential is related to the fact that the chances of a downstream gyrating ion returning to the ramp are higher if the gyration speed is higher, whereas the cross-shock potential takes energy from an ion upon crossing the ramp. The efficiency of in-ramp reflection increases with the increase in the vT∕Vu ratio and the cross-shock potential s (Gedalin et al., 2008; Gedalin, 2016b). It can be most simply explained in the approximation of specular reflection, which ignores magnetic deflection. A particles with initial vx is reflected within the ramp if . For an initial Maxwellian distribution, 5 % of incident ions are reflected if which allows us to define the critical reflection potential (CRP) . In this approximation, in-ramp reflection does not depend on the magnetic compression nor the shock angle and is stronger for lower Mach numbers for given βi and s. In reality, magnetic deflection enhances the reflection, which is never specular. In what follows, we distinguish between reflected and quasi-reflected ions. Figure 4 illustrates the difference between ion populations and the terminology proposed by Gedalin (2016b).
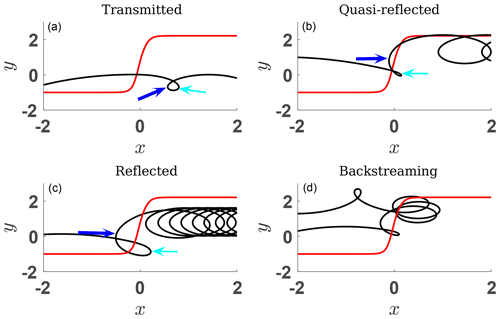
Figure 4Various kinds of x−y trajectories . The magnetic field shape (not to scale) is shown by the red lines, the cyan arrows show first turning point, and the blue arrows show the second turning point.
The first turning point is the first point along the ion trajectory where the sign of vx changes from positive (in the downstream direction) to negative (in the upstream direction). The second turning point is the first point at the ion trajectory where vx changes its sign from negative to positive. A directly transmitted ion may have no turning points at all and may have turning points behind the ramp. Figure 4a shows the trajectory of a directly transmitted ion which does have turning points. In this case, the second turning point, marked using a blue arrow, occurs behind the ramp. The ion trajectory shown in Fig. 4b belongs to a quasi-reflected ion. In this case, the second turning point occurs inside the ramp. For a reflected ion (Fig. 4c), the second turning point is in the upstream region ahead of the ramp. Figure 4d shows, for completeness, a trajectory of a backstreaming ion which has several turning points in the ramp vicinity and eventually escapes in the upstream direction. Quasi-reflected and reflected ions have similar energies and similar gyrating distributions. The difference is that quasi-reflected ions do not appear in the upstream region and do not contribute to foot formation. Each reflected or quasi-reflected ion makes a loop and moves along the shock front. As a result, all of these ions acquire energy in NIF; therefore, they should be clearly distinguished from the directly transmitted ions inside the ramp and behind it, both in a distribution plot and in a spectrogram. In both cases there should be a noticeable gap between the two.
In low-βi and small Bd∕Bu shocks, both modes of reflection should be suppressed. In high Mach number shocks, Bd∕Bu is large, whereas is small unless βi is large. In such shocks, post-ramp reflection should dominate. In marginally critical and weakly supercritical shocks, in-ramp reflection should dominate unless βi is too small. One can expect that in-ramp reflection would cause a sharper drop of the ion pressure and, therefore, a steeper increase in the magnetic field. A more detailed analysis can be carried out numerically where the cross-shock potential s and ion βi are fully controlled.
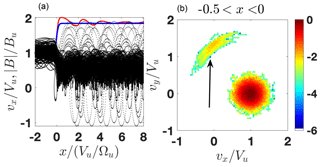
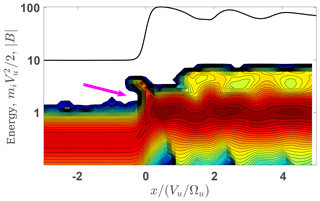
Figure 5(a) The modeled (blue) and the predicted (red) magnetic profiles as well as the ion orbits x vs. vx. (b) A slice of the ion distribution inside the ramp. The shock parameters are M=2.1, , R=1.85, βi=0.2, βe=0.35, and s=0.65. The arrow points to the (quasi-)reflected population.
Figure 5 shows the results of the test-particle adjustment for a shock with βi=0.2 and magnetic compression R=1.85. The adjustment of the downstream magnetic field predicted by the test-particle analysis to the initial model field is achieved with the cross-shock potential s=0.65, which is below the corresponding CGP scr=0.7 but above the corresponding CRP s5 %=0.49. Figure 5a shows a steeper increase toward the overshoot with the first peak exceeding the subsequent peaks. The same panel also shows the ion orbits and Fig. 5b shows a slice of the ion distribution which covers a half of the ramp adjacent to the upstream. Both clearly display the presence of a non-gyrotropic distribution of quasi-reflected ions. The incident and quasi-reflected populations are clearly separated in the velocity space and in energies.
Figure 6 shows the results of the test-particle adjustment for the same compression ratio and cross-shock potential but lower βi=0.05.
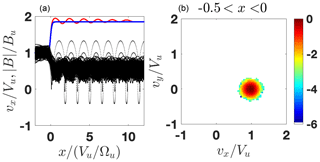
Figure 6(a) The modeled (blue) and the predicted (red) magnetic profiles as well as the ion orbits x vs. vx. (b) A slice of the ion distribution inside the ramp. The shock parameters are M=1.9, , R=1.85, βi=0.05, βe=0.35, and s=0.65.
In this case there are very few quasi-reflected ions and the shock profile follows the low-β prescription shown in Fig. 2a. The magnetic field increase toward the overshoot is less steep and the first peak is shifted further downstream.
Figure 7 shows the results of the test-particle adjustment for the same compression ratio and βi=0.2 but lower cross-shock potential s=0.4.
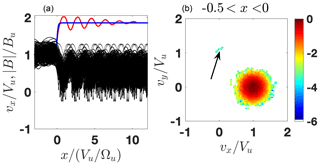
Figure 7(a) The modeled (blue) and the predicted (red) magnetic profiles as well as the ion orbits x vs. vx. (b) A slice of the ion distribution inside the ramp. The shock parameters are M=2.05, , R=1.85, βi=0.2, βe=0.35, and s=0.4. The arrow points to the (quasi-)reflected population.
In this case there are also very few quasi-reflected ions and the shock profile follows the low-β prescription shown in Fig. 2a. The magnetic field increase toward the overshoot is less steep and the first peak is shifted further downstream.
Figure 8 shows the results of the test-particle adjustment for the same compression ratio and βi=0.4 but lower cross-shock potential s=0.4.
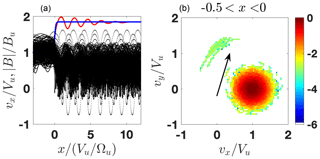
Figure 8(a) The modeled (blue) and the predicted (red) magnetic profiles as well as the ion orbits x vs. vx. (b) A slice of the ion distribution inside the ramp. The shock parameters are M=2.1, , R=1.85, βi=0.4, βe=0.35, and s=0.4. The arrow points to the (quasi-)reflected population.
This value is slightly above the value of s5 %, so that the number of reflected ions is noticeable. Yet, the first maximum is shifted to downstream and the magnetic field increase toward the overshoot is not steep.
A detailed example of a pair of very low-Mach number shocks with the magnetic compression of and βi≈0.08 is given by Pope et al. (2019), Fig. 4, where the cross-shock potentials are also calculated from observations and shown to agree well with the theoretical findings above. Namely, the shock with a lower potential has the first peak higher than the successive peaks, whereas the shock with a higher potential has the second peak higher than the first peak.
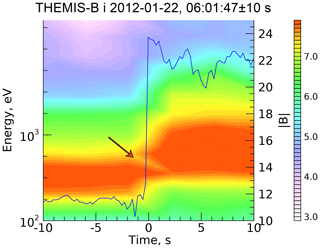
Figure 9 shows the magnetic profile of a of a subcritical shock observed by THEMIS-B plotted over the ion spectrogram. The shock crossing occurred at 22 January 2012, 06:01:47. The estimated shock parameters are similar to those of Fig. 5: , , βi≈0.14, and M=2.6. The corresponding CGP is scr≈0.71 and the CRP is s5 %≈0.64. The spectrogram shows that a number of ions are quasi-reflected at the ramp. This is seen as a gap in the ion distribution inside the ramp. This gap cannot be seen using the standard “tplot” procedure of SPEDAS, as the resolution is low. The IDL function “contour” carries out an interpolation, similar to what is undertaken when calculating distribution functions from a discrete set of measurements in a number of energy channels and angle detectors. With this interpolation, the gap becomes visible. Such quasi-reflection requires a sufficiently high cross-shock potential, capable of stopping slow ions inside the ramp (marked using a red arrow in Fig. 9). The first peak follows a steep magnetic field increase and is the largest. Thus, we expect that , which is in a good agreement with the adjusted value of s=0.65.
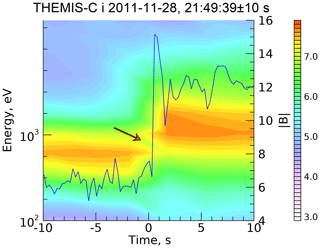
Figure 11Magnetic profile of the 28 November 2011 THEMIS-C-measured shock with the gap in spectrogram due to reflected ions.
Figure 10 shows the corresponding gap for the analyzed shock in Fig. 8. The spectrogram is made in the reference frame (“spacecraft”) moving with the velocity 1.5Vu along the shock normal. Figure 11 shows a similar gap in 28 November 2011 THEMIS-C-measured shock spectrogram in which reflected ions are detected. It is not possible to directly compare the gap for the analyzed shock with observations, as the analysis is carried out in the normal incidence frame whereas the observed spectrograms are produced in the spacecraft frame.
Figure 12 shows the magnetic profile of a THEMIS-C-observed shock. This shock is also subcritical. It has a lower magnetic compression R=1.4 with a slightly higher βi≈0.2. The angle is large , whereas the Mach number is lower M≈1.65. The corresponding CGP is scr≈0.5 and the CRP is s5 %≈0.38. The absence of ions reflected inside the ramp indicates insufficient potential; thus, we expect that s<0.38. Adjustment using the advanced test-particle analysis results in s≈0.35.
Magnetic field measurements at heliospheric shocks are by far the best quality measurements with regard to both precision and resolution. The resolution of particle measurements is much worse: their precision is limited by geometric factors and the finite number of detectors. Measurements of electric field are typically the most difficult. Therefore, any cross-check of less reliable measurements on the basis of better measurements is important. This is particular true if measurements of the magnetic field would enable us to fill gaps in particle and cross-shock measurements that would substantially improve our ability to compare observations and theory.
In the present paper, we examine the implications of the shape of the downstream magnetic oscillation trail for the cross-shock potential. It appears that certain limitations can be placed on the potential using knowledge of the Mach number, magnetic compression, βi, and first peaks of the downstream magnetic field. The two critical kinetic phenomena are the gyration of the center of the incident distribution upon crossing the shock and the onset of ion reflection within the ramp. These two features are related to the two critical values of the cross-shock potential that have been defined in the simplified case of a narrow perpendicular shock. The derived CGP and the CRP are approximations which do not properly take the ramp width and the shock angle into account. Yet, they provide certain limits on possible cross-shock potentials consistent with the measured Mach number, βi, and magnetic compression. Numerical test-particle analyses have shown that these limits are in good agreement with the parameters obtained by adjustment of the predicted profile to the required downstream asymptotic value.
It is found that for the first downstream peak is at the downstream edge of the ramp and is weaker than the second peak. For and for , the first downstream peak is shifted farther downstream and it is the strongest. For , reflected ions are seen, the rise toward the overshoot is substantially steeper, and the first downstream peak is at the downstream edge of the ramp and is the strongest. Thus, observations of the downstream magnetic oscillations may be used to place restrictions on the cross-shock potential. At this stage, the analysis is limited to subcritical, marginally critical, and weakly supercritical shocks. Higher supercriticality will require separate study, also including post-ramp reflected ions.
All data are publicly available and were retrieved using the SPEDAS software (http://spedas.org/blog, last access: 3 January 2020).
MG and XZ contributed to the theory and carried out the observational data analysis. All authors contributed to the discussion and were responsible for writing the paper.
The authors declare that they have no conflict of interest.
Michael Gedalin has been supported by the Israel Science Foundation (grant no. 368/14) and The work of Xiaoyan Zhou was supported by NASA (grant no. NNX17AI26G).
This paper was edited by Peter Wurz and reviewed by two anonymous referees.
Ariad, D. and Gedalin, M.: The role pickup ions play in the termination shock, J. Geophys. Res., 118, 2854–2862, https://doi.org/10.1002/jgra.50170, 2013. a
Balikhin, M. A., Zhang, T. L., Gedalin, M., Ganushkina, N. Y., and Pope, S. A.: Venus Express observes a new type of shock with pure kinematic relaxation, Geophys. Res. Lett., 35, L01103, https://doi.org/10.1029/2007GL032495, 2008. a, b, c
Burgess, D.: Simulations of backstreaming ion beams formed at oblique shocks by direct reflection, Ann. Geophys., 5, 133–146, 1987. a
Burgess, D., Hellinger, P., Gingell, I., and Trávníček, P. M.: Microstructure in two- and three-dimensional hybrid simulations of perpendicular collisionless shocks, J. Plasma Phys., 82, 905820401, https://doi.org/10.1017/S0022377816000660, 2016. a
Dimmock, A. P., Balikhin, M. A., Krasnoselskikh, V. V., Walker, S. N., Bale, S. D., and Hobara, Y.: A statistical study of the cross-shock electric potential at low Mach number, quasi-perpendicular bow shock crossings using Cluster data, J. Geophys. Res., 117, 02210, https://doi.org/10.1029/2011JA017089, 2012. a, b, c
Edmiston, J. P. and Kennel, C. F.: A parametric survey of the first critical Mach number for a fast MHD shock, J. Plasma Phys., 32, 429–441, https://doi.org/10.1017/S002237780000218X, 1984. a, b
Eselevich, V. G., Borodkova, N. L., Eselevich, M. V., Zastenker, G. N., Šafránkova, Y., Nemecek, Z., and Přech, L.: Fine structure of the interplanetary shock front according to measurements of the ion flux of the solar wind with high time resolution, Cosmic Res., 55, 30–45, https://doi.org/10.1134/S0010952517010038, 2017. a
Farris, M., Russell, C., and Thomsen, M.: Magnetic structure of the low beta, quasi-perpendicular shock, J. Geophys. Res., 98, 15285–15294, https://doi.org/10.1029/93JA00958, 1993. a
Gedalin, M.: Ion reflection at the shock front revisited, J. Geophys. Res.h, 101, 4871–4878, https://doi.org/10.1029/95JA03669, 1996. a
Gedalin, M.: Collisionless relaxation of non-gyrotropic downstream ion distributions: dependence on shock parameters, J. Plasma Phys., 81, 905810603, https://doi.org/10.1017/S0022377815001154, 2015. a, b, c
Gedalin, M.: Downstream plasma parameters in laminar shocks from ion kinetics, Phys. Plasmas, 23, 102904, https://doi.org/10.1063/1.4966240, 2016a. a
Gedalin, M.: Transmitted, reflected, quasi-reflected, and multiply reflected ions in low-Mach number shocks, J. Geophys. Res., 121, 10754–10767, https://doi.org/10.1002/2016JA023395, 2016b. a, b, c, d
Gedalin, M. and Dröge, W.: Ion dynamics in quasi-perpendicular collisionless interplanetary shocks: a case study, Front. Phys., 1, 29, https://doi.org/10.3389/fphy.2013.00029, 2013. a
Gedalin, M., Liverts, M., and Balikhin, M. A.: Distribution of escaping ions produced by non-specular reflection at the stationary quasi-perpendicular shock front, J. Geophys. Res., 113, 05101, https://doi.org/10.1029/2007JA012894, 2008. a, b
Gedalin, M., Friedman, Y., and Balikhin, M.: Collisionless relaxation of downstream ion distributions in low-Mach number shocks, Phys. Plasmas, 22, 072301, https://doi.org/10.1063/1.4926452, 2015. a, b, c
Gedalin, M., Zhou, X., Russell, C. T., Drozdov, A., and Liu, T. Z.: Ion dynamics and the shock profile of a low-Mach number shock, J. Geophys. Res., 141, 8913–8923, https://doi.org/10.1029/2018JA025945, 2018. a
Giacalone, J.: The efficient acceleration of thermal protons by perpendicular shocks, Astrophys. J. Lett., 628, L37–L40, https://doi.org/10.1086/432510, 2005. a
Gingell, I., Schwartz, S. J., Burgess, D., Johlander, A., Russell, C. T., Burch, J. L., Ergun, R. E., Fuselier, S., Gershman, D. J., Giles, B. L., Goodrich, K. A., Khotyaintsev, Y. V., Lavraud, B., Lindqvist, P. A., Strangeway, R. J., Trattner, K., Torbert, R. B., Wei, H., and Wilder, F.: MMS observations and hybrid simulations of surface ripples at a marginally quasi-parallel shock, J. Geophys. Res., 77, 11003–11017, https://doi.org/10.1002/2017JA024538, 2017. a
Goodrich, C. C. and Scudder, J. D.: The adiabatic energy change of plasma electrons and the frame dependence of the cross-shock potential at collisionless magnetosonic shock waves, J. Geophys. Res., 89, 6654–6662, https://doi.org/10.1029/JA089iA08p06654, 1984. a
Greenstadt, E. W., Scarf, F. L., Russell, C. T., Formisano, V., and Neugebauer, M.: Structure of the quasi-perpendicular laminar bow shock, J. Geophys. Res., 80, 502–514, https://doi.org/10.1029/JA080i004p00502, 1975. a
Greenstadt, E. W., Scarf, F. L., Russell, C. T., Gosling, J. T., Bame, S. J., Paschmann, G., Parks, G. K., Anderson, K. A., Anderson, R. R., and Gurnett, D. A.: A macroscopic profile of the typical quasi-perpendicular bow shock – ISEE 1 and 2, J. Geophys. Res., 85, 2124–2130, https://doi.org/10.1029/JA085iA05p02124, 1980. a
Johlander, A., Schwartz, S. J., Vaivads, A., Khotyaintsev, Y. V., Gingell, I., Peng, I. B., Markidis, S., Lindqvist, P. A., Ergun, R. E., Marklund, G. T., Plaschke, F., Magnes, W., Strangeway, R. J., Russell, C. T., Wei, H., Torbert, R. B., Paterson, W. R., Gershman, D. J., Dorelli, J. C., Avanov, L. A., Lavraud, B., Saito, Y., Giles, B. L., Pollock, C. J., and Burch, J. L.: Rippled quasiperpendicular shock observed by the Magnetospheric Multiscale Spacecraft, Phys. Rev. Lett., 117, 165101, https://doi.org/10.1103/PhysRevLett.117.165101, 2016. a
Kajdič, P., Blanco-Cano, X., Aguilar-Rodriguez, E., Russell, C. T., Jian, L. K., and Luhmann, J. G.: Waves upstream and downstream of interplanetary shocks driven by coronal mass ejections, J. Geophys. Res., 117, A06103, https://doi.org/10.1029/2011JA017381, 2012. a, b
Kennel, C. F.: Critical Mach numbers in classical magnetohydrodynamics, J. Geophys. Res., 92, 13427–13437, https://doi.org/10.1029/JA092iA12p13427, 1987. a, b
Kucharek, H., Möbius, E., Scholer, M., Mouikis, C., Kistler, L., Horbury, T., Balogh, A., Rème, H., and Bosqued, J.: On the origin of field-aligned beams at the quasi-perpendicular bow shock: multi-spacecraft observations by Cluster, Ann. Geophys., 22, 2301–2308, https://doi.org/10.5194/angeo-22-2301-2004, 2004. a
Lee, M. A., Shapiro, V. D., and Sagdeev, R. Z.: Pickup ion energization by shock surfing, J. Geophys. Res., 101, 4777, https://doi.org/10.1029/95JA03570, 1996. a
Livesey, W. A., Kennel, C. F., and Russell, C. T.: ISEE-1 and -2 observations of magnetic field strength overshoots in quasi-perpendicular bow shocks, Geophys. Res. Lett., 9, 1037–1040, https://doi.org/10.1029/GL009i009p01037, 1982. a
Mellott, M. M. and Greenstadt, E. W.: The structure of oblique subcritical bow shocks – ISEE 1 and 2 observations, J. Geophys. Res., 89, 2151–2161, https://doi.org/10.1029/JA089iA04p02151, 1984. a
Mellott, M. M. and Livesey, W. A.: Shock overshoots revisited, J. Geophys. Res., 92, 13661, https://doi.org/10.1029/JA092iA12p13661, 1987. a
Ofman, L. and Gedalin, M.: Two-dimensional hybrid simulations of quasi-perpendicular collisionless shock dynamics: Gyrating downstream ion distributions, J. Geophys. Res., 118, 1828–1836, https://doi.org/10.1029/2012JA018188, 2013. a
Ofman, L., Balikhin, M., Russell, C. T., and Gedalin, M.: Collisionless relaxation of ion distributions downstream of laminar quasi-perpendicular shocks, J. Geophys. Res., 114, 09106, https://doi.org/10.1029/2009JA014365, 2009. a
Oka, M., Terasawa, T., Saito, Y., and Mukai, T.: Field-aligned beam observations at the quasi-perpendicular bow shock: Generation and shock angle dependence, J. Geophys. Res., 110, A05101, https://doi.org/10.1029/2004JA010688, 2005. a
Pope, S. A., Gedalin, M., and Balikhin, M. A.: The first direct observational confirmation of kinematic collisionless relaxation in very-low Mach number shocks near the Earth, J. Geophys. Res., 165, 3–15, https://doi.org/10.1029/2018JA026223, 2019. a, b, c
Russell, C., Hoppe, M., Livesey, W., and Gosling, J.: ISEE-1 and-2 observations of laminar bow shocks- Velocity and thickness, Geophys. Res. Lett., 9, 1171, https://doi.org/10.1029/GL009i010p01171, 1982a. a
Russell, C. T., Hoppe, M. M., and Livesey, W. A.: Overshoots in planetary bow shocks, Nature, 296, 45–48, https://doi.org/10.1029/GL009i010p01171, 1982b. a
Russell, C. T., Jian, L. K., Blanco-Cano, X., and Luhmann, J. G.: STEREO observations of upstream and downstream waves at low Mach number shocks, Geophys. Res. Lett., 36, 03106, https://doi.org/10.1029/2008GL036991, 2009. a, b
Scholer, M., Kucharek, H., and Kato, C.: On ion injection at quasiparallel shocks, Phys. Plasmas, 9, 4293–4300, https://doi.org/10.1063/1.1508441, 2002. a
Schwartz, S. J., Thomsen, M. F., Bame, S. J., and Stansberry, J.: Electron heating and the potential jump across fast mode shocks, J. Geophys. Res., 93, 12923–12931, https://doi.org/10.1029/JA093iA11p12923, 1988. a
Sckopke, N., Paschmann, G., Bame, S. J., Gosling, J. T., and Russell, C. T.: Evolution of ion distributions across the nearly perpendicular bow shock – Specularly and non-specularly reflected-gyrating ions, J. Geophys. Res., 88, 6121–6136, https://doi.org/10.1029/JA088iA08p06121, 1983. a
Scudder, J. D., Aggson, T. L., Mangeney, A., Lacombe, C., and Harvey, C. C.: The resolved layer of a collisionless, high beta, supercritical, quasi-perpendicular shock wave, I – Rankine-Hugoniot geometry, currents, and stationarity, J. Geophys. Res., 91, 11019–11052, https://doi.org/10.1029/JA091iA10p11019, 1986. a, b
SPEDAS: SPEDAS software, available at: http://spedas.org/blog, last access: 3 January 2019.
Wilson, L. B. I., Koval, A., Szabo, A., Breneman, A., Cattell, C. A., Goetz, K., Kellogg, P. J., Kersten, K., Kasper, J. C., Maruca, B. A., and Pulupa, M.: Observations of electromagnetic whistler precursors at supercritical interplanetary shocks, Geophys. Res. Lett., 39, L08109, https://doi.org/10.1029/2012GL051581, 2012. a
Wilson, L. B., Sibeck, D. G., Breneman, A. W., Contel, O. L., Cully, C., Turner, D. L., Angelopoulos, V., and Malaspina, D. M.: Quantified energy dissipation rates in the terrestrial bow shock: 1. Analysis techniques and methodology, J. Geophys. Res., 119, 6455–6474, https://doi.org/10.1002/2014JA019929, 2014. a
Wilson III, L. B., Koval, A., Szabo, A., Stevens, M. L., Kasper, J. C., Cattell, C. A., and Krasnoselskikh, V. V.: Revisiting the structure of low-Mach number, low-beta, quasi-perpendicular shocks, J. Geophys. Res., 81, 2097, https://doi.org/10.1002/2017JA024352, 2017. a
Zank, G., Pauls, H., Cairns, I., and Webb, G.: Interstellar pickup ions and quasi-perpendicular shocks: Implications for the termination shock and interplanetary shocks, J. Geophys. Res., 101, 457–477, https://doi.org/10.1029/95JA02860, 1996. a
Zilbersher, D. and Gedalin, M.: Pickup ion dynamics at the structured quasi-perpendicular shock, Plan. Sp. Sci., 45, 693–703, https://doi.org/10.1016/S0032-0633(97)00030-5, 1997. a