the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
On modelling the kinematics and evolutionary properties of pressure-pulse-driven impulsive solar jets
Balveer Singh
Kushagra Sharma
Abhishek K. Srivastava
In this paper, we describe the kinematical and evolutionary properties of the impulsive cool jets in the solar atmosphere using numerical simulation by Godunov-type PLUTO code at two different quiet-Sun magnetic field strengths (B=56 gauss and B=112 gauss). These types of chromospheric jets originate due to a pressure pulse, which mimics the after-effects of the localized heating in the lower solar atmosphere. These jets may be responsible for the transport of mass and energy in the localized upper atmosphere (i.e. corona). The detection of the height–time profiles for the jets, which were developed by imposing different pressure pulses, exhibit asymmetric near-parabolic behaviour. This infers that the upward motion of the jet occurs under the influence of pressure perturbation. However, its downward motion is not only governed by the gravitational free fall, but also by the complex plasma motions near its base under the effect of counter-propagating pulses. The maximum height and lifetime of the jets with respect to the strength of the pressure pulse show a linear increasing trend. This suggests that if the extent of the heating and, thus, the pressure perturbations are longer, then more longer chromospheric jets can be triggered from the same location in the chromosphere. For a certain amplitude of pressure pulse, the strong magnetic field configuration (B=112 gauss) leads to more longer jets compared with the weaker field (B=56 gauss). This suggests that the strong magnetic field guides the pressure-pulse-driven jets more efficiency towards the higher corona. In conclusion, our model mimics the properties and evolution of the variety of the cool impulsive jets in the chromosphere (e.g. macrospicules, network jets, isolated repeated cool jets, confined and small surges, and so on.).
- Article
(2672 KB) - Full-text XML
- BibTeX
- EndNote
Observations reveal that various types of plasma jets are ubiquitous in the solar atmosphere at diverse spatio-temporal scales (e.g. Sterling, 2000; Katsukawa et al., 2007; Shibata et al., 2007; Nisticò et al., 2009; Wedemeyer-Böhm et al., 2012; Tian et al., 2014; Raouafi et al., 2016; Kayshap et al., 2018, and references cited therein). These jets may play a significant role in transporting energy and mass in the localized upper atmosphere (i.e. corona) of the Sun. As far as the complex magnetic structuring of the solar chromosphere is concerned, it triggers various types of cool plasma jets (e.g. spicules, macrospicules, surges, magnetic swirls, network jets, evolution of plasma twists, and so on.), which attribute to the association of exotic wave and plasma processes (e.g. De Pontieu et al., 2004, 2007, 2014; McIntosh et al., 2011; Wedemeyer-Böhm et al., 2012; Tian et al., 2014; Kayshap et al., 2018; Srivastava et al., 2017, 2018, and references cited therein).
In the recent observations, it has been found that a quiet solar chromosphere triggers various kinds of localized solar jets (e.g. magnetic swirls, network jets, spicule-like rotating plasma structures, and so on.) in addition to the typical spicules (e.g. Wedemeyer-Böhm et al., 2012; Tian et al., 2014; Shetye et al., 2016, and references cited therein). Moreover, solar macrospicules, confined surges, anemone jets, and so on are other flowing magnetic structures that are typically observed in the solar chromosphere (e.g. Roy, 1973; Wilhelm, 2000; Morita et al., 2010, and references cited therein). The evolution of such a variety of chromospheric jets at diverse spatio-temporal scales provides a very detailed picture of the ongoing different plasma processes triggering these jets in an abundant measure in the localized solar atmosphere (e.g. De Pontieu et al., 2004, 2007; McIntosh et al., 2011; Kayshap et al., 2013b, 2018; Murawski et al., 2011, 2018; Srivastava et al., 2017, 2018; Martínez-Sykora et al., 2017; Iijima and Yokoyama, 2017; Liu et al., 2019, and references cited therein).
It is well established that complex magnetic structuring of the solar chromosphere enables small-scale magnetic reconnection and, thus, the localized heating and generation of the solar jets (e.g. Yokoyama and Shibata, 1995). However, the height of the reconnection and its magnitude decides the evolution of the inherent physical processes. If the reconnection occurs in the chromosphere, then the evolution of the shocks and plasma motions may be evident (e.g. Shibata et al., 1992; Kayshap et al., 2013a, and references cited therein). However, the reconnection height lying in the inner corona may result in the jet propagation due to the direct influence of the Lorentz force, and Alfvén waves can also be evolved (e.g. Nishizuka et al., 2008; Jelínek et al., 2015, and references cited therein).
Recently, observations and modelling of the chromosphere has revealed that many localized jets (e.g. spicules and macrospicules, network jets, confined surges, jets in the twisted or straight magnetic spires, chromospheric jets near flare ribbons, and so on.) exhibit brightening and heating at their footpoints before their evolution (e.g. Isobe et al., 2007; Murawski et al., 2011; Uddin et al., 2012; Kayshap et al., 2013b, 2018; Li et al., 2019, and references cited therein). There may also be shock-related brightening in the lower solar atmosphere at the site of the evolution of such jets. Martínez-Sykora et al. (2011) and Judge et al. (2012) studied the structure and evolution of the spicule-like jets that are triggered by the pulses which are launched in the vertical velocity component from the upper chromosphere. The vertical velocity pulse is converted into a shock that propagates in the upward direction and chromospheric plasma follows these shocks to form the jet (e.g. Martínez-Sykora et al., 2009; McIntosh, 2007, and references cited therein). These shock-driven jets show a thin linear plasma structure that reaches a few megametres above the chromosphere and can transport mass and energy in the overlying solar atmosphere. Kuźma et al. (2017) also proposed the two fluid spicule model. These spicules are triggered by the velocity pulse in vertical direction, while radiative cooling and thermal conduction do not play any significant role in the dynamics of such plasma ejecta. Recent observations have revealed that the network jets are associated with the impulsive origin in the chromosphere (e.g. Kayshap et al., 2018), and they morphologically overlap with each other and with type I/type II spicules as well in the quiet-Sun chromosphere (e.g. Tian et al., 2014). In the present paper, we present a model of the pressure-pulse-driven jets and their evolutionary properties, which may mimic the variety of impulsive chromospheric jets (e.g. macro spicules, network jets, confined smaller jet-like surges of moderate length, and so on.) originating at the top of the photosphere. The pressure pulse acts as a driver, mimicking that heating has already occurred locally and has activated the pressure perturbations launching these jets. We have estimated typical parameters (height, width, and lifetime) of the jets triggered by different pressure pulses. The kinematics and evolutionary properties of such jets have also been estimated for two quiet-Sun magnetic field strengths and a comparison has been made. In Sect. 2, we describe the magnetohydrodynamics (MHD) model of the jet, the equilibrium model of the solar atmosphere, perturbations, and numerical methods. The results are described in Sect. 3. The discussion and conclusions are outlined in the last section.
In order to model the pressure-pulse-driven solar jets in the quiet-Sun, we consider and implement a gravitationally stratified and magnetized solar atmosphere. This atmosphere is approximated by the ideal MHD equations in their conservative form as outlined below (e.g. Mignone et al., 2007, 2012; Wołoszkiewicz et al., 2014):
In the above representation of the set of ideal MHD equations, the symbol ρ depicts mass density in the solar atmosphere, v denotes the velocity, B is the magnetic field satisfying divergence free condition, and μ depicts the magnetic permeability. The parameter defines the total pressure, which is an addition of thermal (p) and magnetic (B2∕2μ) pressure. I is a 3×3 unit matrix. The quantity E describes the total energy, which is given as follows in Eq. (2) (e.g. Mignone et al., 2007, 2012; Wołoszkiewicz et al., 2014):
In this equation, γ is the specific heat ratio. PLUTO code also satisfies an ideal gas equation under the MHD approximation.
In Eq. (3), T symbolizes temperature, and kB is the Boltzmann constant. The symbol m denotes the mean particle mass. We take a typical value of m for the model atmosphere that is equal to 1.24. We do not consider non-ideal conditions such as the velocity of the background plasma flows, dissipative effects like viscosity and resistivity, magnetic diffusivity, cooling and/or heating of the plasma, because we are interested in understanding the kinematics and evolutionary properties of these pressure-driven jets. We consider ∇⋅B to be equal to zero or a very negligible values of it in the numerical domain.
2.1 Equilibrium model of the solar atmosphere
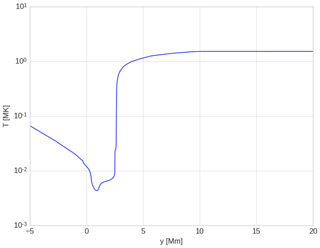
We consider the numerical simulation box mimicking a realistic solar atmosphere covering the region from the photosphere to the inner corona. In the case of the initial solar atmosphere subjected to the hydrostatic equilibrium, the realistic temperature profile Te(y) is shown in Fig. 2, which is inferred from the observed line profiles by Avrett and Loeser (2008) and also depicted in Konkol et al. (2012) and Wołoszkiewicz et al. (2014).
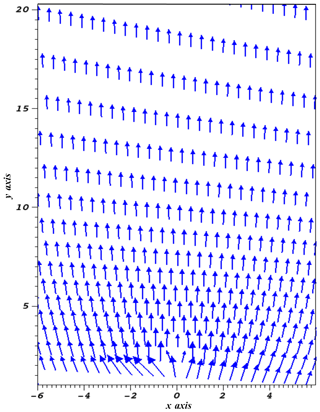
Figure 1Equilibrium open and expanding magnetic field lines in the model quiet-Sun solar atmosphere. The x axis and the y axis are given in megametres (Mm).
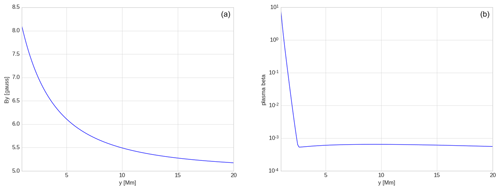
Figure 3Magnetic field profile (a) and plasma beta profile (b) vs. height (y) in the model quiet solar atmosphere.
In the case of the static equilibrium of the solar atmosphere, i.e. when there is no background initial flows (Ve=0), it is approximated as a force-free as well as a current-free magnetic field. Therefore, we can abbreviate the initial magnetic field condition as
In the given expression, the subscript “e” represents the equilibrium quantities. The vector magnetic potential can be estimated with the magnetic flux function given as (Konkol et al., 2012; Wołoszkiewicz et al., 2014)
where the magnetic flux function is given as follows:
Here Bref is the strength of the pole, and a and b collectively determine its position. In the above-mentioned expression, we fix the vertical coordinate of magnetic pole at Mm in the convection zone. The jet is triggering from the chromosphere (1.8 Mm) along the open magnetic field lines and the pulse is initially lunched there. Thus, there is no dynamics occurring in the convection zone related to the evolution of these isolated chromospheric jets. Our realistic temperature model (Fig. 2) smoothly extends from the convection zone to the photosphere; thereafter, it couples to the chromosphere, the transition region (TR), and corona. In order to save on computing time, we do set the lower boundary of the simulation box at the photosphere. For the sake of visualization, we have already given the magnetic field variations in the plot (see Fig. 1 for B=112 gauss pole strength) starting from the photosphere to the corona. It clearly shows that the magnetic pole is set somewhere deeper in the convection zone, and that the magnetic field is smoothly extended into the solar atmosphere at higher heights with an exponential decay. Putting the pole deep below in the convection zone is a requirement of the numerical simulation, as we keep the magnetic singularity away from the simulation box in order to set an appropriate initial force- and current-free magnetic atmosphere. The quiet-Sun cool chromospheric jets are simulated in our model. We set the source magnetic field of a typical order in the quiet Sun. Moreover, the chosen magnetic fields smoothly extend to the inner corona and appropriately set reasonable values of plasma beta and the Alfvén speed (Figs. 3, 5). This helps with the evolution of the perturbations and the launch of the collimated jets. In this model, we chose two different magnetic field strength configurations, i.e. B=56 gauss and B=112 gauss. The reference level is taken in the overlying corona at yref=10 Mm. The magnetic field lines exhibit open and expanding field behaviour, as shown in Fig. 1. We take the magnetic field strength typical of the regions of the Sun where chromospheric jets are formed in the quiet Sun.
In the hydrostatic equilibrium of the solar atmosphere set in the simulation box, the gravity force balances the pressure gradient force. This can be written as follows:
Here we keep the value of g fixed at 27 400.0 cm s−2. Using the vertical component of the hydrostatic equilibrium in the model solar atmosphere and the ideal gas law, we determine the equilibrium plasma gas pressure and mass density as follows (Konkol et al., 2012; Wołoszkiewicz et al., 2014):
where
In these expressions, Pref is the gas pressure at reference level yref, which is attributed as the pressure scale height.
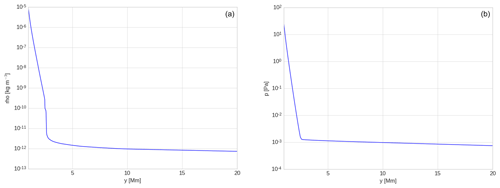
Figure 4Equilibrium profiles of mass density (a) and gas pressure (b) vs. height in the model quiet solar atmosphere.
For considering the gravitationally stratified and longitudinally structured solar atmosphere, we obtain the plasma temperature profile Te(y) which is derived by Avrett and Loeser (2008) and displayed in Fig. 2. It should be noted that the typical value of the temperature Te(y) at the top of the photosphere is about 5700 K. This temperature corresponds to y=0.5 Mm at the photosphere, and it falls gradually and attains its minimum of about 4350 K at higher altitudes of approximately y=0.95 Mm which represents a temperature minimum. As we move higher up in the solar atmosphere, Te(y) increases gradually with height up to the transition region which is located at y≃2.7 Mm. Te(y) sharply increases up to the corona and finally attains a constant value of mega-Kelvin at the coronal heights, as shown in Fig. 2.
The magnetic field and plasma beta at y=2.7 Mm (at the transition region) are 6.884 gauss and 0.0005 respectively; they grow with the depth and attain 7.646 gauss and 0.219 respectively at y=1.5 Mm, which is located within the chromosphere (Fig. 3).
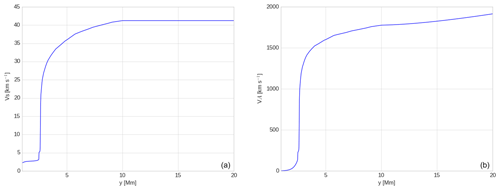
Using Eq. (8), we obtain the equilibrium mass density and gas pressure profiles with respect to height (Fig. 4). We found that the equilibrium mass density and gas pressure at 2.7 Mm (at the transition region) are kg m−3 and Pa respectively. They grow with depth and attain kg m−3 and Pa respectively at y=1.5 Mm, which is located within the chromosphere. Figure 5 shows the trend of the Alfvén speed and sound speed with respect to height in the solar atmosphere. The Alfvén speed is calculated by , which is 1015.583 km s−1 at y=2.7 Mm (i.e. transition region), whereas it decrease with the depth and attains 6.167 km s−1 at y=1.5 Mm located within the chromosphere. The sound speed calculated by at the transition region, i.e. 2.7 Mm, is 21.392 km s−1, whereas it decreases with depth and attains 2.638 km s−1 within the chromosphere at y=1.5 Mm.
These background physical quantities (i.e. density, pressure, magnetic field plasma beta, Alfvén speed and sound speed) for the model gravitationally stratified and magnetized solar atmosphere are appropriately set in the model solar atmosphere. We show these profiles for the atmosphere that have source magnetic field value of 112 gauss. The various physical quantities, their values, and variations with the height (y) in the structured solar atmosphere clearly indicate their smooth extension into the inner corona. Their reasonable values are set for the model atmosphere, and are appropriate for launching the perturbations and associated jets.
Perturbations
We consider the initial solar atmosphere to be in hydrostatic equilibrium and to be gravitationally stratified. We perturb the equilibrium atmosphere by the initial pulse in the vertical direction in equilibrium gas pressure. The Gaussian form of the pressure pulse in the vertical direction is given as follows:
Here (x0,y0) is the initial position of the pressure pulse, w is the width of the pulse, and Ap denotes the pressure amplitude. We fix the values of x0 and y0 at 0 and 1.8 Mm respectively, thereby launching the pressure perturbations in the chromosphere. We set w equal to 0.2 Mm. We imply different pressure pulse strengths of Ap = 4–22, which account for the generation of the variety of solar jets.
Observations reveal that these types of chromospheric jets are found to be associated with an impulsive origin in the chromosphere, and their footpoints are usually associated with brightening. The chosen pressure pulses in this modelling mimic the after-effect of the heating scenario at their footpoints before evolution. This is not a direct implementation of heating, as we use the ideal set of MHD equations in the numerical simulation. However, the Gaussian pressure pulse implies the disturbance that represents the response in the form of the pressure perturbations once the underlying heating episode is completed. This perturbation locally alters the equilibrium and generates the propagating disturbances. The pressure pulse is chosen with varying amplitude Ap = 4–22 in order to understand the evolutionary and propagation properties of the cool chromospheric jets. We perform the numerical simulation at two magnetic fields strengths (i.e. B=56 and 112 gauss), typical of quiet-Sun atmosphere.
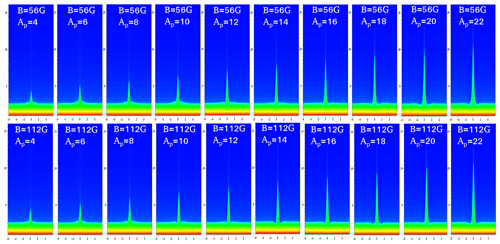
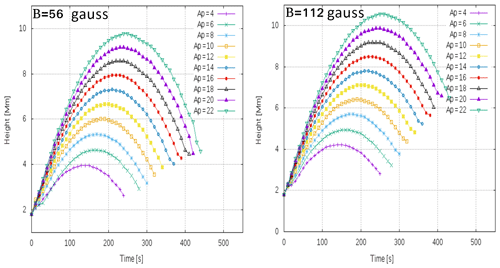
Figure 6Evolution of the plasma jets at different pressure pulses at two different magnetic field strengths, B=56 gauss and B=112 gauss. The mosaic diagram shows the maximum height of the evolved jets at different pressure pulses, e.g. Ap = 4–22. The horizontal (x) and vertical (y) axes are shown in megametres (Mm).
2.2 Numerical methods
PLUTO code is a Godunov-type, non-linear, finite-volume/finite-difference code which takes ideal and non-ideal sets of governing equations into account (Mignone et al., 2007, 2012; Wołoszkiewicz et al., 2014). It is constructed to numerically integrate a system of conservation laws, which can be shown as follows:
In this equation, U denotes a set of conservative physical fields (e.g. magnetic field, density, velocity, pressure, and so on.); F(U) is the flux tensor and S(U) is the source term.
PLUTO code utilizes a second-order unsplit Godunov solver and adaptive mesh refinement (AMR) of the system of conservation laws as shown in Eq. (11). In order to numerically solve the set of ideal MHD equations (Eq. 1), we set the simulation box as (−6, 6) Mm × (1, 21) Mm. This represents a realistic localized solar atmosphere with a span of 12 and 20 Mm in the horizontal and vertical directions respectively. This solar atmosphere is constructed within the simulation box and all four boundary conditions by fixing the simulation region to their equilibrium values. Numerical simulation is carried out with double-precision arithmetic using multiple passage interface (MPI) (Mignone et al., 2007). The eight processors are used in the parallel calculations. It took approximately 12 h of CPU time for each set of calculations. We adopted a static uniform grid which was divided into 384 equal cells in the x direction. We also adopted a static uniform and stretched grid which were divided into 128 equal cells and 256 equal cells respectively in the y direction. The resolution of the simulation domain was 31 km per numerical cell. We obtained the numerical simulation data every 10 s.
In our modelling, we set the Courant–Friedrichs–Lewy (CFL) number equal to 0.25. We used the Roe solver for the flux computation, which is a linearized Riemann solver based on the characteristic decomposition of the Roe matrix (cf. Mignone et al., 2007, 2012).
The pressure perturbations in the solar chromosphere launch the thin and localized plasma jets (Fig. 6). These jets carry the mass from the chromosphere to the outer corona along the expanding open field lines. The pressure perturbations mimic the impulsive origin of these jets due to the localized heating episodes that might occur at some time epoch in the solar chromosphere and that cause the direct pressure disturbance in the equilibrium atmosphere. As the pressure pulse is launched, the plasma gets essential velocity perturbations guided along the vertical and expanding field lines. These perturbations are converted into magneto-acoustic shocks in the stratified atmosphere which are followed by the motion of cool plasma. Shock leaves the domain quickly, and the resulting after-effect is the formation of the jet. The pressure-pulse-driven cool jets depend on the amplitude of the initial pulse (Ap) as well as the height that it is triggered at. This further converts into the acoustic shocks that trigger plasma in the upward direction. A low-pressure region is created behind the slow magneto-acoustic shock, which drives the cool plasma from the chromosphere upward mimicking cool jet. Therefore, the amplitude of the pressure pulse as well as its triggering site are important factors upon which the evolution of the jets depend. In this model, we studied chromospheric cool jets in order to be able to take a certain amplitude of the pressure pulse at the chromospheric height below the TR to generate these plasma ejecta.
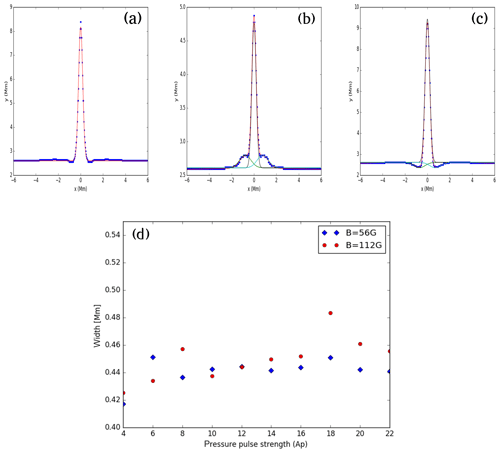
Figure 10(a, b, c) The example spatial profiles of various jets when they reach their respective maximum height. Panels (a), (b), and (c) show spatial profiles of the jet at B=56 gauss and Ap=16, B=56 gauss and Ap=6, and B=112 gauss and Ap=18 respectively. As the base of these jets exhibits a complex shape, the triple or single Gaussian profiles are fitted and the respective full width half maximums (FWHMs) are estimated after determining the Gaussian width. (d) The width of the jets vs. the pressure pulse strength (Ap) in the solar atmosphere for the B=56 gauss (blue diamonds) and B=112 gauss (red circles) magnetic fields. The FWHMs of various jets lie between 0.42 and 0.48 Mm. They show a mild increasing trend for both of the magnetic fields.
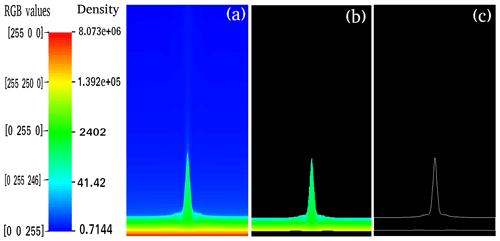
We analysed the kinematical and evolutionary properties of these pressure-pulse-driven solar jets by their detection (Fig. 7). Figure 8 displays the height–time profile of various jets at two different magnetic field configurations (B=56 gauss and B=112 gauss). It shows that the jets exhibit asymmetric parabolic paths, which are different from the normal parabolic path of any ejecta in the gravitational field. We develop a code in MATLAB to find the height of the single isolated jet with time and its termination point. To calculate the height of the jet, we took the time series of the numerical simulation data (Fig. 7a). In this density map, we estimate the assigned RGB values corresponding to the density variations over the colour scales. The highest density corresponds to a fixed value of green, G=255, and the value decreases towards blue (B), moving towards the tip of the jet with decreasing density. Ultimately the value becomes 245 as the jet ends. The value fades away slowly and there is no sharp boundary, so we take B=245 as the approximate boundary value for the jet. We used this observation to calculate the required parameters by fixing G=255 and B≥245; we then generated a masked image with only G=255 and B≤245, and the rest of the portion was left as black (Fig. 7b). Next, we generated the contour of the masked image to generate Fig. 7c; thereafter, we found the height variations automatically with respect to time. We used the snapshots of the density map for the calculation of height when the jet had reached above the transition region, and the snapshots of the pressure map for the calculation of the height of the jet when it was below the transition region. Also, at time t=0 s, we took the value of the height as 1.8 Mm, as was set in the simulation. The lifetime of the isolated jet is estimated in the masked time series where only the jet's motion is visible. We calculate the time when the height of the jet again starts increasing after the fall, and this point is considered to be the termination point of the first isolated jet. For Ap=14 (time = 190 s and corresponding density map), we demonstrated the above-mentioned procedure, in Fig. 7, to detect the jet.
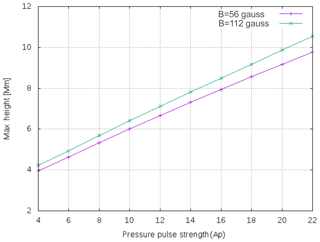
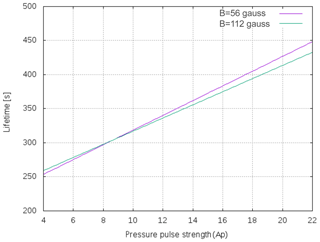
We investigate the evolution of the pulses and associated jets at two different magnetic field strengths (B=56, 112 gauss). The automatically detected height–time profiles for the jets, generated by imposing different pressure pulses, clearly exhibit the asymmetric near-parabolic profiles (Fig. 8). This infers that the upward motion of the jet under the influence of pressure perturbations does occur, however, its downward motion is not singly governed by the gravitational free fall. The downward-propagating counterpart of the perturbation, when reflecting from the photosphere, goes up and causes interaction with the falling jet plasma. This creates the complex scenario near the base of the jet, where we observe the complex plasma motion and evolution of the multiple jets one by one (e.g. Murawski et al., 2011; Kayshap et al., 2018; Li et al., 2019). We aim to study the evolution of the first isolated jet that is generated due to the forward-propagating component of the disturbance. The down-draughting disturbance is usually weak when moving towards the denser lower solar atmosphere; therefore, it is not seen well in the form of significant density perturbations below in the density maps. However, its effect can be visible once it rebounds back a certain later time and helps in the formation of the secondary jets and interaction with the falling material of the first jet. We study the propagation and evolutionary properties of the first upward-propagating isolated jet (at different pressure pulse strengths and different magnetic field strengths); therefore, we do not consider other secondary jets and their evolution. Figure 9 displays an interesting correlation between the maximum height of the jets and strength of the pressure pulse, which shows a linearly increasing trend. This directly infers that if the extent of the heating and, thus, the pressure perturbations is higher then more longer jets can be generated from the same location in the chromosphere. For the strong magnetic field, the height of the jet will be longer at a particular pressure pulse strength compared with the same for the weaker magnetic field strength. The width of the jets may be determined by the conservation of mass in the cross section of the flowing jet spire, although many other factors, i.e. the configuration of the magnetic field, the interaction of counter-propagating disturbances near the base of the jet, and so on, can affect its value. The width of the jets is measured using a Gaussian fit to the spatial profile of the jets when they attain maximum height. The example spatial profiles of various jets when they reach at their respective maximum heights are shown in Fig. 10a–c. As the base of these jets exhibits complex shape and motions, the triple or single Gaussian profiles are fitted on their spatial profiles and the respective FWHMs are estimated after determining the fitted Gaussian width. The width of the jets vs. the pressure pulse strength (Ap) in the solar atmosphere for the B=56 gauss (blue diamonds) and B=112 gauss (red circles) magnetic fields are shown in Fig. 10d. The FWHMs of various jets lie between 0.42 and 0.48 Mm, although, they exhibit a mild increasing trend on average for both the magnetic fields. The lifetime of the jets shows linear variation and a positive slope with respect to the pressure pulse strength (Fig. 11). This scenario depicts that more localized energy released into the chromosphere results in more larger perturbations that, in turn, lead to longer jets with long lifetimes. Moreover, the lifetime of the jet for a particularly larger pressure pulse strength will be smaller in the presence of a strong magnetic field and vice-versa (Ap≥10). However, in our simulation under the given initial condition, the lifetime is almost same for the two magnetic field strengths, particularly at low amplitude pressure perturbations (Ap≤10).
There are several jets in the chromosphere, such as macrospicules, network jets, isolated repeated jets, and confined surges (e.g. Wilhelm, 2000; Murawski et al., 2011; Uddin et al., 2012; Kayshap et al., 2013a, 2018; Li et al., 2019, and references cited therein). The common resemblance point in the evolution of these jets is the presence of heating at their base. Sometimes these jets are so abundant that they over-impose on the co-spatial presence of classical chromospheric ejecta like type I and type II spicules (Tian et al., 2014). Therefore, we can not ignore the role of such episodic jets in determining the mass and the energy transport in the corona. It should be noted that we attempt here to model the above-mentioned episodic and impulsive jets in terms of their kinematical and evolutionary properties. However, we exclude the classical chromospheric spicules (type I and type II), spicule-like structures, anemone jets, an so on in this physical model as they may require additional driving mechanisms for their launch and in the non-linear regime complex plasma flows, and wave activity may present there (e.g. De Pontieu et al., 2004; Shetye et al., 2016; Srivastava et al., 2017; Martínez-Sykora et al., 2017, and references cited therein). Therefore, we only include those jets and their kinematical properties in our model that evolve due to heating at their footpoints and the associated pressure pulse.
It should be noted that our results demonstrate that the elongation and lifetime of these jets are directly proportional to the heating pulse, and their shape depends upon the complex plasma motions near their base as well as magnetic field configurations of their spire. Therefore, we generally see brightening and mass motions starting at their base, and the evolution of the plasma motion occurs at the jet's spire. Our model represents the formation of such chromospheric jets which evolve due to pressure perturbations near their footpoints. The pressure-pulse-driven jets are most likely driven by the localized heating at their footpoints that lie in the lower solar atmosphere. These perturbations are converted into magneto-acoustic shocks when they move up in the stratified solar atmosphere. The low-pressure region created behind the shock is followed by the motion of cool plasma along the field lines that form the jet. The wave-driven jets are usually launched by the evolution of both the magnetic and the plasma perturbations. When the velocity, as well as pressure perturbations, are launched higher in the solar atmosphere, they can generate MHD modes in the structured solar atmosphere. In the case of only the Lorentz magnetic force and the related velocity perturbations, the Alfvén modes can be generated. These waves under the non-linear effects can also be associated with the ponderomotive force guiding vertical plasma flows in form of jets (e.g. Murawski et al., 2018). The strong magnetic field guides more longer jets with a comparatively shorter lifetime, particularly at large pressure perturbations (Figs. 9, 11). However, the widths of these jets for different pressure pulse strengths lie within the range of 0.42 to 0.48 Mm for strong (e.g. B=112 gauss) and weaker (e.g. B=56 gauss) magnetic fields (Fig. 10). Although, we present the kinematics and evolutionary properties of a single isolated jet, usually sites where pressure perturbations do occur exhibit the formation of multiple jets associated with significant brightening at their base. Such locations are very common sites for the origin of the impulsive generation of isolated chromospheric jets, as mentioned above.
The numerical simulation data are available from the lead author.
All authors have contributed in a equal manner.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Solar magnetism from interior to corona and beyond”. It is a result of the Dynamic Sun II: Solar Magnetism from Interior to Corona, Siem Reap, Angkor Wat, Cambodia, 12–16 February 2018.
The authors acknowledge the UKIERI research grant provided by the University Grant Commission (UGC), India, and the British Council, UK, for support of the current research. They also thankfully acknowledge support from Piotr Konkol and Kris Murawski from UMCS, Lublin, Poland, for providing realistic solar atmosphere data to incorporate into the PLUTO code. Balveer Singh acknowledges the Human Resource Development Group (HRDG) of the Council of Scientific & Industrial Research (CSIR) for providing him with a research scholar grant. Balveer Singh also thanks the Department of Physics at the Indian Institute of Technology (BHU) for providing him with research facilities. The authors also wish to thank both of the referees for their constructive comments and the editor Sergiy Shelyag for his valuable remarks that improved the paper. Finally, the authors acknowledge the use of PLUTO code in the present work.
This paper was edited by Sergiy Shelyag and reviewed by two anonymous referees.
Avrett, E. H. and Loeser, R.: Models of the Solar Chromosphere and Transition Region from SUMER and HRTS Observations: Formation of the Extreme-Ultraviolet Spectrum of Hydrogen, Carbon, and Oxygen, Astrophys. J., 175, 229–276, https://doi.org/10.1086/523671, 2008. a, b
De Pontieu, B., Erdélyi, R., and James, S. P.: Solar chromospheric spicules from the leakage of photospheric oscillations and flows, Nature, 430, 536–539, https://doi.org/10.1038/nature02749, 2004. a, b, c
De Pontieu, B., McIntosh, S. W., Carlsson, M., Hansteen, V. H., Tarbell, T. D., Schrijver, C. J., Title, A. M., Shine, R. A., Tsuneta, S., Katsukawa, Y., Ichimoto, K., Suematsu, Y., Shimizu, T., and Nagata, S.: Chromospheric Alfvénic Waves Strong Enough to Power the Solar Wind, Science, 318, 1574, https://doi.org/10.1126/science.1151747, 2007. a, b
De Pontieu, B., Rouppe van der Voort, L., McIntosh, S. W., Pereira, T. M. D., Carlsson, M., Hansteen, V., Skogsrud, H., Lemen, J., Title, A., Boerner, P., Hurlburt, N., Tarbell, T. D., Wuelser, J. P., De Luca, E. E., Golub, L., McKillop, S., Reeves, K., Saar, S., Testa, P., Tian, H., Kankelborg, C., Jaeggli, S., Kleint, L., and Martinez-Sykora, J.: On the prevalence of small-scale twist in the solar chromosphere and transition region, Science, 346, 1255732, https://doi.org/10.1126/science.1255732, 2014. a
Iijima, H. and Yokoyama, T.: A Three-dimensional Magnetohydrodynamic Simulation of the Formation of Solar Chromospheric Jets with Twisted Magnetic Field Lines, Astrophys. J., 848, 38, https://doi.org/10.3847/1538-4357/aa8ad1, 2017. a
Isobe, H., Tripathi, D., and Archontis, V.: Ellerman Bombs and Jets Associated with Resistive Flux Emergence, Astrophys. J. Lett., 657, L53–L56, https://doi.org/10.1086/512969, 2007. a
Jelínek, P., Srivastava, A. K., Murawski, K., Kayshap, P., and Dwivedi, B. N.: Spectroscopic observations and modelling of impulsive Alfvén waves along a polar coronal jet, Astron. Astrophys., 581, A131, https://doi.org/10.1051/0004-6361/201424234, 2015. a
Judge, P. G., de Pontieu, B., McIntosh, S. W., and Olluri, K.: The Connection of Type II Spicules to the Corona, Astrophys. J., 746, 158, https://doi.org/10.1088/0004-637X/746/2/158, 2012. a
Katsukawa, Y., Berger, T. E., Ichimoto, K., Lites, B. W., Nagata, S., Shimizu, T., Shine, R. A., Suematsu, Y., Tarbell, T. D., Title, A. M., and Tsuneta, S.: Small-Scale Jetlike Features in Penumbral Chromospheres, Science, 318, 1594, https://doi.org/10.1126/science.1146046, 2007. a
Kayshap, P., Srivastava, A. K., and Murawski, K.: The Kinematics and Plasma Properties of a Solar Surge Triggered by Chromospheric Activity in AR11271, Astrophys. J., 763, 24, https://doi.org/10.1088/0004-637X/763/1/24, 2013a. a, b
Kayshap, P., Srivastava, A. K., Murawski, K., and Tripathi, D.: Origin of Macrospicule and Jet in Polar Corona by a Small-scale Kinked Flux Tube, Astrophys. J. Lett., 770, L3, https://doi.org/10.1088/2041-8205/770/1/L3, 2013b. a, b
Kayshap, P., Murawski, K., Srivastava, A. K., and Dwivedi, B. N.: Rotating network jets in the quiet Sun as observed by IRIS, Astron. Astrophys., 616, A99, https://doi.org/10.1051/0004-6361/201730990, 2018. a, b, c, d, e, f, g
Konkol, P., Murawski, K., and Zaqarashvili, T. V.: Numerical simulations of magnetoacoustic oscillations in a gravitationally stratified solar corona, Astron. Astrophys., 537, A96, https://doi.org/10.1051/0004-6361/201117943, 2012. a, b, c
Kuźma, B., Murawski, K., Zaqarashvili, T. V., Konkol, P., and Mignone, A.: Numerical simulations of solar spicules: Adiabatic and non-adiabatic studies, Astron. Astrophys., 597, A133, https://doi.org/10.1051/0004-6361/201628747, 2017. a
Li, X., Zhang, J., Yang, S., and Hou, Y.: Flow Instabilities in Solar Jets in Their Upstream and Downstream Regimes, Astrophys. J., 875, 52, https://doi.org/10.3847/1538-4357/ab0f39, 2019. a, b, c
Liu, J., Nelson, C. J., Snow, B., Wang, Y., and Erdélyi, R.: Evidence of ubiquitous Alfvén pulses transporting energy from the photosphere to the upper chromosphere, Nature Commun., 10, 3504, https://doi.org/10.1038/s41467-019-11495-0, 2019. a
Martínez-Sykora, J., Hansteen, V., and Carlsson, M.: Twisted Flux Tube Emergence from the Convection Zone to the Corona. II. Later States, Astrophys. J., 702, 129–140, https://doi.org/10.1088/0004-637X/702/1/129, 2009. a
Martínez-Sykora, J., Hansteen, V., and Moreno-Insertis, F.: On the Origin of the Type II Spicules: Dynamic Three-dimensional MHD Simulations, Astrophys. J., 736, 9, https://doi.org/10.1088/0004-637X/736/1/9, 2011. a
Martínez-Sykora, J., De Pontieu, B., Hansteen, V. H., Rouppe van der Voort, L., Carlsson, M., and Pereira, T. M. D.: On the generation of solar spicules and Alfvénic waves, Science, 356, 1269–1272, https://doi.org/10.1126/science.aah5412, 2017. a, b
McIntosh, S. W.: Does High Plasma-β Dynamics “Load” Active Regions?, Astrophys. J. Lett., 657, L125–L129, https://doi.org/10.1086/513105, 2007. a
McIntosh, S. W., de Pontieu, B., Carlsson, M., Hansteen, V., Boerner, P., and Goossens, M.: Alfvénic waves with sufficient energy to power the quiet solar corona and fast solar wind, Nature, 475, 477–480, https://doi.org/10.1038/nature10235, 2011. a, b
Mignone, A., Bodo, G., Massaglia, S., Matsakos, T., Tesileanu, O., Zanni, C., and Ferrari, A.: PLUTO: A Numerical Code for Computational Astrophysics, Astrophys. J., 170, 228–242, https://doi.org/10.1086/513316, 2007. a, b, c, d, e
Mignone, A., Zanni, C., Tzeferacos, P., van Straalen, B., Colella, P., and Bodo, G.: The PLUTO Code for Adaptive Mesh Computations in Astrophysical Fluid Dynamics, Astrophys. J., 198, 7, https://doi.org/10.1088/0067-0049/198/1/7, 2012. a, b, c, d
Morita, S., Shibata, K., UeNo, S., Ichimoto, K., Kitai, R., and Otsuji, K.-I.: Observations of Chromospheric Anemone Jets with Hinode Ca II Broadband Filtergraph and Hida Ca II Spectroheliograph, Publ. Astron. Soc. Jpn., 62, 901–920, https://doi.org/10.1093/pasj/62.4.901, 2010. a
Murawski, K., Srivastava, A. K., and Zaqarashvili, T. V.: Numerical simulations of solar macrospicules, Astron. Astrophys., 535, A58, https://doi.org/10.1051/0004-6361/201117589, 2011. a, b, c, d
Murawski, K., Kayshap, P., Srivastava, A. K., Pascoe, D. J., Jelínek, P., Kuźma, B., and Fedun, V.: Magnetic swirls and associated fast magnetoacoustic kink waves in a solar chromospheric flux tube, Mon. Not. R. Astron. Soc., 474, 77–87, https://doi.org/10.1093/mnras/stx2763, 2018. a, b
Nishizuka, N., Shimizu, M., Nakamura, T., Otsuji, K., Okamoto, T. J., Katsukawa, Y., and Shibata, K.: Giant Chromospheric Anemone Jet Observed with Hinode and Comparison with Magnetohydrodynamic Simulations: Evidence of Propagating Alfvén Waves and Magnetic Reconnection, Astrophys. J. Lett., 683, L83, https://doi.org/10.1086/591445, 2008. a
Nisticò, G., Bothmer, V., Patsourakos, S., and Zimbardo, G.: Characteristics of EUV Coronal Jets Observed with STEREO/SECCHI, Sol. Phys., 259, 87–108, https://doi.org/10.1007/s11207-009-9424-8, 2009. a
Raouafi, N. E., Patsourakos, S., Pariat, E., Young, P. R., Sterling, A. C., Savcheva, A., Shimojo, M., Moreno-Insertis, F., DeVore, C. R., Archontis, V., Török, T., Mason, H., Curdt, W., Meyer, K., Dalmasse, K., and Matsui, Y.: Solar Coronal Jets: Observations, Theory, and Modeling, Space Sci. Rev., 201, 1–53, https://doi.org/10.1007/s11214-016-0260-5, 2016. a
Roy, J. R.: The Magnetic Properties of Solar Surges, Sol. Phys., 28, 95–114, https://doi.org/10.1007/BF00152915, 1973. a
Shetye, J., Doyle, J. G., Scullion, E., Nelson, C. J., Kuridze, D., Henriques, V., Woeger, F., and Ray, T.: High-cadence observations of spicular-type events on the Sun, Astron. Astrophys., 589, A3, https://doi.org/10.1051/0004-6361/201527505, 2016. a, b
Shibata, K., Ishido, Y., Acton, L. W., Strong, K. T., Hirayama, T., Uchida, Y., McAllister, A. H., Matsumoto, R., Tsuneta, S., Shimizu, T., Hara, H., Sakurai, T., Ichimoto, K., Nishino, Y., and Ogawara, Y.: Observations of X-ray jets with the YOHKOH Soft X-ray Telescope, Publ. Astron. Soc. Jpn., 44, L173–L179, 1992. a
Shibata, K., Nakamura, T., Matsumoto, T., Otsuji, K., Okamoto, T. J., Nishizuka, N., Kawate, T., Watanabe, H., Nagata, S., UeNo, S., Kitai, R., Nozawa, S., Tsuneta, S., Suematsu, Y., Ichimoto, K., Shimizu, T., Katsukawa, Y., Tarbell, T. D., Berger, T. E., Lites, B. W., Shine, R. A., and Title, A. M.: Chromospheric Anemone Jets as Evidence of Ubiquitous Reconnection, Science, 318, 1591, https://doi.org/10.1126/science.1146708, 2007. a
Srivastava, A. K., Shetye, J., Murawski, K., Doyle, J. G., Stangalini, M., Scullion, E., Ray, T., Wójcik, D. P., and Dwivedi, B. N.: High-frequency torsional Alfvén waves as an energy source for coronal heating, Sci. Rep.-UK, 7, 43147, https://doi.org/10.1038/srep43147, 2017. a, b, c
Srivastava, A. K., Murawski, K., Kuźma, B., Wójcik, D. P., Zaqarashvili, T. V., Stangalini, M., Musielak, Z. E., Doyle, J. G., Kayshap, P., and Dwivedi, B. N.: Confined pseudo-shocks as an energy source for the active solar corona, Nature Astronomy, 2, 951–956, https://doi.org/10.1038/s41550-018-0590-1, 2018. a, b
Sterling, A. C.: Solar Spicules: A Review of Recent Models and Targets for Future Observations – (Invited Review), Sol. Phys., 196, 79–111, https://doi.org/10.1023/A:1005213923962, 2000. a
Tian, H., DeLuca, E. E., Cranmer, S. R., De Pontieu, B., Peter, H., Martínez-Sykora, J., Golub, L., McKillop, S., Reeves, K. K., Miralles, M. P., McCauley, P., Saar, S., Testa, P., Weber, M., Murphy, N., Lemen, J., Title, A., Boerner, P., Hurlburt, N., Tarbell, T. D., Wuelser, J. P., Kleint, L., Kankelborg, C., Jaeggli, S., Carlsson, M., Hansteen, V., and McIntosh, S. W.: Prevalence of small-scale jets from the networks of the solar transition region and chromosphere, Science, 346, 1255711, https://doi.org/10.1126/science.1255711, 2014. a, b, c, d, e
Uddin, W., Schmieder, B., Chandra, R., Srivastava, A. K., Kumar, P., and Bisht, S.: Observations of Multiple Surges Associated with Magnetic Activities in AR 10484 on 2003 October 25, Astrophys. J., 752, 70, https://doi.org/10.1088/0004-637X/752/1/70, 2012. a, b
Wedemeyer-Böhm, S., Scullion, E., Steiner, O., Rouppe van der Voort, L., de La Cruz Rodriguez, J., Fedun, V., and Erdélyi, R.: Magnetic tornadoes as energy channels into the solar corona, Nature, 486, 505–508, https://doi.org/10.1038/nature11202, 2012. a, b, c
Wilhelm, K.: Solar spicules and macrospicules observed by SUMER, Astron. Astrophys., 360, 351–362, 2000. a, b
Wołoszkiewicz, P., Murawski, K., Musielak, Z., and Mignone, A.: Numerical simulations of Alfvén waves in the solar atmosphere with the PLUTO code, Control Cybern., 43, 321–335, 2014. a, b, c, d, e, f
Yokoyama, T. and Shibata, K.: Magnetic reconnection as the origin of X-ray jets and Hα surges on the Sun, Nature, 375, 42–44, https://doi.org/10.1038/375042a0, 1995. a