the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Geomagnetic conjugate observations of ionospheric disturbances in response to a North Korean underground nuclear explosion on 3 September 2017
Yi Liu
Qiong Tang
Guanyi Chen
Zhengyu Zhao
We report observations of ionospheric disturbances in response to a North Korean underground nuclear explosion (UNE) on 3 September 2017. By using data from IGS (International GNSS Service) stations and Swarm satellites, geomagnetic conjugate ionospheric disturbances were observed. The observational evidence showed that UNE-generated ionospheric disturbances propagated radially from the UNE epicenter with a velocity of ∼280 m s−1. We propose that the ionospheric disturbances are results of electrodynamic process caused by LAIC (lithosphere–atmosphere–ionosphere coupling) electric field penetration. The LAIC electric field can also be mapped to the conjugate hemispheres along the magnetic field line and consequently cause ionospheric disturbances in conjugate regions. The UNE-generated LAIC electric field penetration plays an important role in the ionospheric disturbances in the region of the nuclear test site nearby and the corresponding geomagnetic conjugate points.
Ionospheric disturbances can be generated by various natural processes such as geomagnetic storms, internal electrodynamic instabilities and so forth. Furthermore, human activity can also cause evident ionospheric disturbances. Although an underground nuclear explosion (UNE) detonates deep in the lithosphere, ionospheric disturbances related to the UNE can also be observed. By using Global Navigation Satellite System – Total Electron Content (GNSS-TEC) observations, Park et al. (2011) reported that traveling ionospheric disturbances (TIDs) with a phase velocity of ∼273 m s−1 were generated by a UNE in the 25 May 2009 North Korean UNE test. They proposed that acoustic gravity waves (AGWs) generated by the UNE can propagate to ionosphere and cause wavelike disturbances.
While the observations of UNE-related ionospheric disturbances have been discussed in Park et al. (2011, 2013), further investigation is still required to understand the mechanism(s) of ionospheric disturbance generation. Lithosphere–atmosphere–ionosphere coupling (LAIC) mechanisms originally proposed to interpret the linkage between ionospheric disturbances and earthquake activities are the most likely explanation for the ionospheric disturbances in response to the UNE. The AGW theory is one part of LAIC mechanisms (Liu et al., 2016; Maruyama et al., 2016). AGWs excited by the unusual events in lithosphere such as an earthquake or an UNE can propagate to ionospheric height and generate TIDs and electromagnetic disturbances (Gokhberg et al., 1990; Pokhotelov et al., 1994, 1995, 1999; Mikhailov et al., 2000; Huang et al., 2011; Jonah et al., 2017). However, the AGW mechanism cannot fully explain all the observations related to earthquakes. The electrostatic coupling is another candidate for LAIC mechanisms. During earthquakes, LAIC electric field or current can be excited by complex physical and chemical reactions induced by rock rupture and penetrate the ionosphere to promote plasma disturbances by E×B motion (Xu et al., 2011; Zhao and Hao, 2015). Zhou et al. (2017) developed an electric field penetration model for LAIC and their simulation results showed that the penetration height of the LAIC electric field can reach 400 km in midlatitude regions. Because of high electric conductivity along the geomagnetic field lines, LAIC electric field can also be mapped along geomagnetic field lines and cause ionospheric disturbances at the geomagnetic conjugate points (Ruzhin et al., 1998; Zhang et al., 2009; Li and Parrot, 2017).
In this study, we have used magnetic conjugate GNSS observations and Swarm satellites to investigate the LAIC electric penetration effects of the North Korean UNE on 3 September 2017.
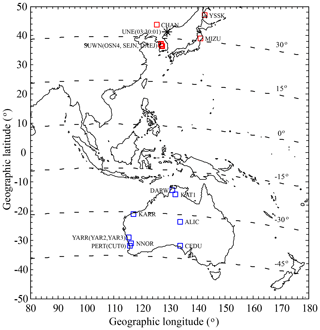
Figure 1The positions of UNE and IGS stations. The position of 3 September 2017 North Korean UNE is represented by a black star. The locations of IGS stations in both hemispheres are represented by red and blue squares. Lines of constant geomagnetic latitude are represented by black dashed lines.
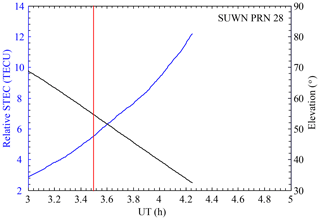
Figure 2An example of the time series of relative STEC obtained by SUWN using satellite PRN 28 between 03:00 and 05:00 UT on 3 September 2017. The explosion time is represented by the red line.
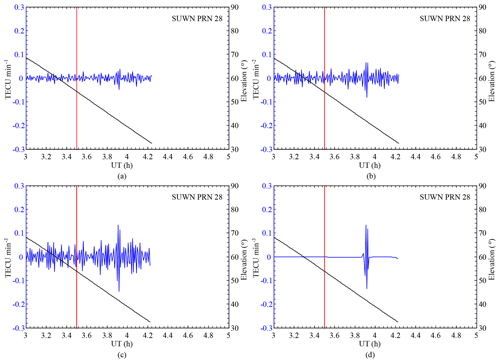
Figure 3The time sequences of derivatives of relative STEC obtained by the SUWN station using satellite PRN 28 between 03:00 and 05:00 UT on 3 September 2017: (a) first-order derivatives, (b) second-order derivatives, (c) third-order derivatives and (d) wavelet de-noised third-order derivatives. The explosion time is represented by the red line.
The IGS (International GNSS Service) stations used in this study are located in East Asia and Australia. The geographical positions of the UNE and the IGS stations are shown in Fig. 1. In order to eliminate the noise and multipath effects of GPS signals, only carrier phase observations are utilized to derive the relative slant total electron content (STEC). The time resolution is about 30 s. The ionospheric pierce point (IPP) height in this study is assumed to be 350 km. Figure 2 shows an example of the time series of relative STEC obtained by IGS station SUWN using satellite pseudorandom noise (PRN) 28 between 03:00 and 05:00 UT on 3 September 2017. To calculate the ionospheric disturbances related to a UNE from GNSS observations, the main trends of relative STEC strongly influenced by the Sun's diurnal cycle need to be removed. In this study, the numerical third-order horizontal three-point derivatives of relative STEC are used to extract the ionospheric disturbances (Park et al., 2011). In the first step, the numerical first-order horizontal three-point derivatives are taken as follows:
where si is the ith data point, δsi is the first derivative and n is the number of relative STEC observations. The main relative STEC trends are removed through this process. Figure 3a shows the time series of first-order derivatives of relative STEC. Waves with small amplitudes occurred at around hours 3.9 and 4.1, even though it was not certain whether they were meaningful signals or just noises. The numerical derivative formula is repeatedly performed on relative STEC derivatives to extract the ionospheric disturbances related to the UNE. The second-order derivatives can be written in the following expression:
where δδsi is the second derivative and m is the number of first derivative observations. Figure 3b shows the time series of second-order derivatives of relative STEC. Compared to the first-order derivatives presented in Fig. 3a, the amplitude around hour 3.9 was amplified, while others were not significant. The third-order derivatives are given as follows:
where δδδsi is the third derivatives and l is the number of second derivative observations. Figure 3c shows the time series of third-order derivatives of relative STEC. Compared to the second-order derivatives presented in Fig. 3b, the disturbances around hour 3.9 were further amplified. Therefore, compared to the standard first derivatives, the numerical third-order horizontal-point derivatives can emphasize the more significant wave components with small amplitudes. Moreover, to further remove the background noises of third-order derivatives of relative STEC, the Haar wavelet decomposition process is applied to the third-order derivatives. Equations (4) and (5) give the Haar wavelet function and scale function, respectively.
Figure 3d shows the wavelet de-noised third-order derivatives. From Fig. 3d, it was found that the background noises in Fig. 3c were completely removed and only valuable wave components were retained.
The Swarm mission operated by the European Space Agency (ESA) mainly focuses on the survey of the global geomagnetic field and its temporal evolution. The Swarm mission consists of three satellites named Alpha (A), Bravo (B) and Charlie (C). By using the magnetic field data detected by Vector Field Magnetometer (VFM) on Swarm, the ionospheric radial current (IRC) density could be calculated by using the spatial gradient of residual magnetic field data through Ampère's law (Ritter et al., 2013). The field-aligned current (FAC) density could be also obtained by the ratio of the IRC density to the sine of the magnetic inclination angle. The FAC density and IRC density used in the study were provided by the Swarm level 2 dataset with a time resolution of 1 s. The ionospheric current disturbances associated with a UNE can also be calculated by the above method.
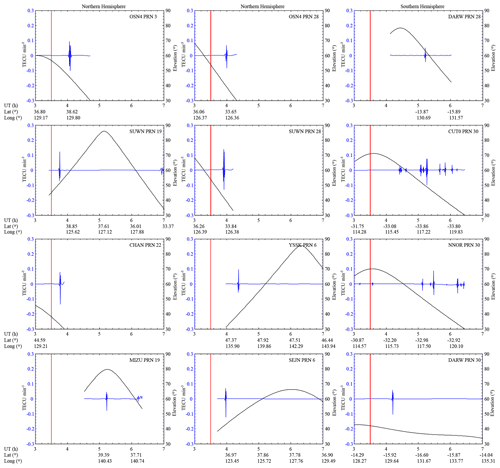
Figure 4The time sequences of three-order derivatives of carrier-phase-derived relative STEC by GNSS observations from different IGS stations in East Asia (left and middle column) and Australia (right column) on 3 September 2017. The blue lines indicate the wavelet de-noised three-order derivative of relative STEC. The black lines indicate the GPS signal's elevation between the GNSS satellite and IGS stations. The explosion time is represented by the red line.
According to the measurements of the China Earthquake Network Center (CENC), the approximate location of the UNE on 3 September 2017 is at 41.35∘ N and 129.11∘ E. The explosion time was at 03:30:01 UTC. The geomagnetic Kp index was less than 3 and the auroral electrojet (AE) index was less than 500 nT before and after the UNE, which indicates that the geomagnetic activity was not very great.
Figure 4 shows the time sequences of third-order derivatives of carrier-phase-derived relative STEC by GNSS observations from different IGS stations in East Asia and Australia on 3 September 2017. All the GNSS observations from the Northern and Southern Hemisphere showed obvious short-period fluctuations within 2 h after the UNE. It was also found that the time delay after the UNE was different according to different IPPs of GPS signals. Figure 5 presents the IPP tracks of relative STEC derivatives. In order to investigate the propagation velocity of ionospheric disturbances, we assumed that the UNE-generated ionospheric disturbances propagate radially with a certain velocity.
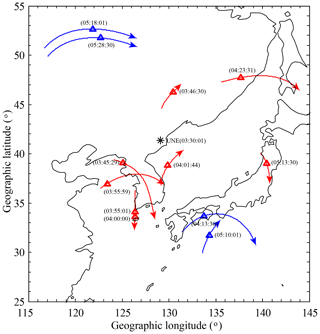
Figure 5The IPP tracks of relative STEC derivatives. The red lines indicate the IPP tracks obtained by IGS stations in the Northern Hemisphere. The blue lines indicate the magnetic conjugate positions of the IPP tracks obtained by IGS stations in the Southern Hemisphere. The positions of the maximum amplitudes of relative STEC derivatives in the Northern Hemisphere are represented by red triangles. The geomagnetic conjugate positions of the maximum amplitudes of relative STEC derivatives in the Southern Hemisphere are represented by blue triangles.
Figure 6 illustrates the satellite Swarm B ionospheric current derivatives. Compared to observed results of ionospheric currents in quiet time, it was seen that the FAC derivatives and IRC derivatives at conjugate hemispheres both showed obvious short-period fluctuations after the UNE. The ionospheric current disturbances could reach 0.5 µA m−2 s−3.
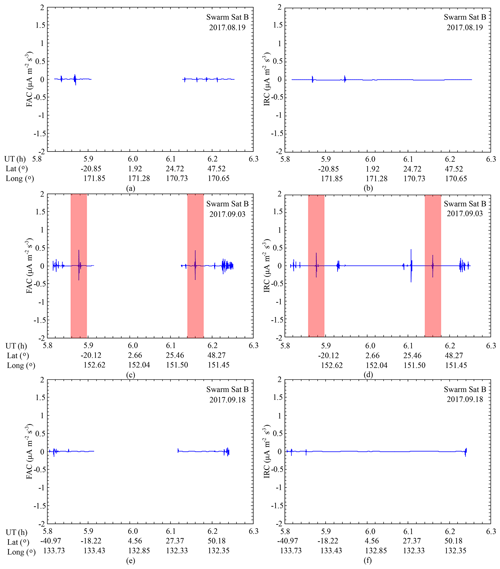
Figure 6Results of Swarm B ionospheric current data analysis for the 2017 UNE: (a), (c) and (e) are the FAC; (b), (d) and (f) are the IRC. From top to bottom, they indicate observations of Swarm B on 19 August 2017 (quiet time), 3 September 2017 (UNE time) and 18 September 2017 (quiet time). The ionospheric current disturbances in response to the UNE are represented by the red rectangles.
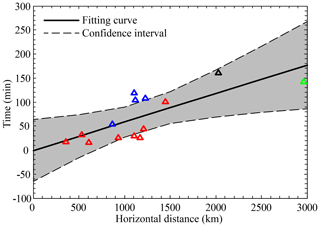
Figure 7Horizontal distance–time data for the UNE-generated ionospheric disturbances. The black line indicates the fitting curve obtained by the least square method. The gray lines represent the boundaries of 95 % confidence intervals. The red and blue triangles have the same meaning as in Fig. 5. The black triangle represents the position of ionospheric current disturbances in the Northern Hemisphere. The green triangle represents the geomagnetic conjugate position of ionospheric current disturbances in the Southern Hemisphere.
Based on the UNE–IPP horizontal distances and the ionospheric disturbances arrival time, the horizontal propagation velocity of ionospheric disturbances could be estimated by linear fitting model. The horizontal distance from IPPs to the epicenter and time delay of the UNE-generated ionospheric disturbances (STEC disturbances and ionospheric current disturbances) are presented in Fig. 7. The black triangle and green triangle presented in Fig. 7 represent the position of ionospheric current disturbances in the Northern Hemisphere and the geomagnetic conjugate position of ionospheric current disturbances in the Southern Hemisphere, respectively. The value of the horizontal velocity obtained by the least square estimation was ∼280 m s−1.
By utilizing geomagnetic conjugate GNSS TEC observations and ionospheric current products from Swarm, we introduced the ionospheric disturbances which are regarded as a result of the UNE carried out by North Korea on 3 September 2017. The method of the numerical third-order horizontal three-point derivatives was applied to the GNSS TEC and the ionospheric current of Swarm to extract the ionospheric disturbances, which can also be found in Park et al. (2011). Ionospheric disturbances derived from GNSS TEC observations in our study are consistent with the results of the North Korean UNE on 25 May 2009 obtained by Park et al. (2011).
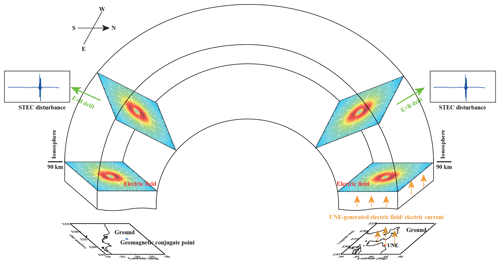
Figure 8A sketch of the geomagnetic conjugate effect related to the UNE in the region of the nuclear test site nearby and the corresponding geomagnetic conjugate region.
The effects of a UNE on the ionosphere could be very similar to that of earthquakes on the ionosphere. In previous studies, AGWs are regarded as the most likely mechanism for atmospheric and ionospheric disturbances excited by a UNE or earthquakes (Mikhailov et al., 2000; Che et al., 2009; Garrison et al., 2010; Park et al., 2011, 2013; Yang et al., 2012; Maruyama et al., 2016). Klimenko et al. (2011) proposed that the ionospheric disturbances were generated by small-scale internal gravity waves (IGWs) through propagation and dissipation processes during seismic activity. Liu et al. (2016), and Chum et al. (2016, 2018) suggested that coseismic ionospheric disturbances could be generated by long-period infrasound waves excited by seismic waves. Based on GNSS receiver observations over the Brazilian sector, Jonah et al. (2017) presented daytime medium-scale traveling ionospheric disturbances (MSTIDs) observed in the conjugate hemispheres. They proposed that the gravity-wave-induced polarized electric fields could map into the conjugate hemisphere and further generate ionospheric disturbances in conjugate regions. However, compared with TEC disturbances induced by MSTIDs presented in Jonah et al. (2017), ionospheric disturbances in response to the North Korean UNE in both hemispheres were smaller and ended within 5 min in our work. Therefore, electric field disturbances induced by UNE-generated TEC disturbances presented in Fig. 4 may be very small and cannot generate obvious ionospheric disturbances in conjugate region.
Recent research has shown that earthquake ionospheric disturbances could be attributed not only to the AGW mechanism but also to the electrostatic coupling, which means the electric field or current penetration into the ionosphere induced by earthquakes. Based on the observations of the INTERCOSMOS-BULGARIA-1300 satellite and the DEMETER satellite, Gousheva et al. (2008, 2009) and Zhang et al. (2014) reported ionospheric quasi-static electric field perturbations during seismic activity. By using the magnetometer observations, Hao et al. (2013) and Liu et al. (2016) showed obvious ionospheric current and magnetic field perturbations after the Tohoku earthquake. They proposed that the seismo-traveling atmospheric disturbances (STADs) caused by infrasonic waves can propagate vertically into the ionosphere and modify the E layer Hall and Pedersen conductivity, resulting in background ionospheric electric field and magnetic field disturbances. Pulinets et al. (2000) proposed a quasi-electrostatic model for the LAIC mechanism. The simulation results indicated that the abnormal electric field induced by an earthquake can penetrate into the ionosphere to cause the ionospheric electric field disturbances (Sorokin et al., 2001). The enhancement of TEC at the epicenter and its geomagnetic conjugate points were reported by Liu et al. (2011), which indicated that the earthquake-generated electric field penetration can be mapped along geomagnetic field lines to promote ionospheric disturbances at its conjugate points by electrodynamic process through E×B drift. Therefore, the geomagnetic conjugation effects of ionospheric disturbances in Fig. 4 can be explained by the UNE-generated electric field penetration. A schematic sketch of geomagnetic conjugate effect related to the UNE in the region of the nuclear test site nearby and the corresponding geomagnetic conjugate region is shown in Fig. 8. The UNE-generated electric field or current penetrates the ionosphere and further generates an abnormal electric field at ionospheric altitude. The distribution of the ionospheric electric field showed in Fig. 8 was calculated by the LAIC electric field penetration model proposed by Zhou et al. (2017). Because of the high conductivity of the geomagnetic field, the abnormal ionospheric electric field could be mapped along geomagnetic field lines. Geomagnetic conjugate ionospheric disturbances could be generated by an abnormal ionospheric electric field through E×B drift. Our study provides observational evidence of LAIC electric penetration rather than the acoustic gravity wave mechanism.
Geomagnetic conjugate observations in the ionosphere have been reported by a few researchers. Otsuka et al. (2002, 2004) reported simultaneous observations of equatorial airglow depletions and medium-scale TIDs at geomagnetic conjugate points in both hemispheres by two all-sky imagers. Their results also suggested that the polarization electric field, which is important for airglow depletion and MSTIDs generation, can be mapped along the field lines.
In our observations, we found that the ionospheric disturbances in both hemispheres caused by the UNE-generated electric field penetration propagated radially at a velocity of roughly 280 m s−1 in Figs. 5 and 7. The LAIC electric field can be roughly estimated to be 14.5 mV m−1, which is consistent with the magnitude of the earthquake-generated ionospheric electric field presented by Zhang et al. (2014). Figure 6 presents the results of the ionospheric current disturbances detected by the satellite Swarm B after the UNE. The reason may be that the ionospheric disturbances from the UNE propagate here to generate the current disturbances by electrodynamic processes.
Moreover, compared with the magnitude and timescale of ionospheric disturbances caused by earthquakes, there are inconsistencies in our study. Based on IGS station observations around Tibet and Nepal, Kong et al. (2018) reported that TEC disturbances exceeded 0.3 TEC units (TECUs) and lasted for 15–20 min during the 2015 Nepal earthquake. However, it was found that the UNE-generated ionospheric disturbances were relatively smaller and ended within 5 min in Fig. 4. The reason for the difference between TEC disturbances may be that earthquake magnitude and background ionosphere are different.
In this study, we have shown that the geomagnetic conjugate observations of GNSS TEC and the ionospheric current from Swarm can be regarded as a response to the North Korean UNE on 3 September 2017. The LAIC electric penetration effects of UNE have been discussed in detail. The main results are summarized as follows:
-
The ionospheric TEC and current disturbances were observed in both hemispheres after the UNE. According to the spatiotemporal relation, UNE-generated ionospheric disturbances propagated radially from the explosion epicenter with a velocity of ∼280 m s−1.
-
The ionospheric disturbances may be caused by LAIC electric penetration rather than AGWs. The LAIC electric field induced by the UNE penetrates the ionosphere and causes plasma density disturbances near the nuclear test site and its conjugate points by electrodynamic processes.
This study is based on the dataset provided by the IGS (International GNSS Service) and Swarm satellites. The data of IGS stations can be downloaded from http://www.igs.gnsswhu.cn/index.php/Home/DataProduct/igs.html (last access: 16 May 2019) or some other IGS data centers. The data of Swarm satellites can be downloaded from ftp://swarm-diss.eo.esa.int/ (last access: 16 May 2019).
QT and GC downloaded the IGS data and Swarm satellite data. YL provided the algorithm and analyzed the data. YL, CZ, and ZZ discussed observational results. YL and CZ prepared the manuscript with contributions from all co-authors.
The authors declare that they have no conflict of interest.
We thank the IGS Data Center of Wuhan University (http://www.igs.gnsswhu.cn/index.php/Home/DataProduct/igs.html, last access: 16 May 2019) for the use of GPS-TEC data. We also acknowledge the ESA for the Swarm data (ftp://swarm-diss.eo.esa.int/, last access: 16 May 2019).
This research has been supported by the National Natural Science Foundation of China (grant nos. 41574146 and 41774162).
This paper was edited by Dalia Buresova and reviewed by four anonymous referees.
Che, I.-Y., Kim, T. S., Jeon, J.-S., and Lee, H.-I.: Infrasound observation of the apparent North Korean nuclear test of 25 May 2009, Geophys. Res. Lett., 36, L22802, https://doi.org/10.1029/2009GL041017, 2009.
Chum, J., Cabrera, M. A., Mošna, Z., Fagre, M., Baše, J., and Fišer, J.: Nonlinear acoustic waves in the viscous thermosphere and ionosphere above earthquake, J. Geophys. Res.-Space, 121, 12126–12137, https://doi.org/10.1002/2016JA023450, 2016.
Chum, J., Liu, J.-Y., Podolská, K., and Šindelářová, T.: Infrasound in the ionosphere from earthquakes and typhoons, J. Atmos. Sol. Terr. Phy., 171, 72–82, 2018.
Garrison, J. L., Yang, Y.-M., and Lee, S.-C.: Observations of ionospheric disturbances coincident with North Korean underground nuclear tests, Abstract SA43B-1754 presented at 2010 Fall Meeting, AGU, 13–17 December 2010, San Francisco, Calif., 2010.
Gokhberg, M. B., Pilipenlco, V. A., Pokhotelov, O. A., and Partasaraty, S.: Acoustic disturbance induced by underground nuclear explosion as source of electrostatic turbulence in the magnetosphere, Doklady AN SSSR, 313, 568–574, 1990.
Gousheva, M., Danov, D., Hristov, P., and Matova, M.: Quasi-static electric fields phenomena in the ionosphere associated with pre- and post earthquake effects, Nat. Hazards Earth Syst. Sci., 8, 101–107, https://doi.org/10.5194/nhess-8-101-2008, 2008.
Gousheva, M., Danov, D., Hristov, P., and Matova, M.: Ionospheric quasi-static electric field anomalies during seismic activity in August–September 1981, Nat. Hazards Earth Syst. Sci., 9, 3–15, https://doi.org/10.5194/nhess-9-3-2009, 2009.
Hao, Y. Q., Xiao, Z., and Zhang, D. H.: Teleseismic magnetic effects (TMDs) of 2011 Tohoku earthquake, J. Geophys. Res.-Space, 118, 3914–3923, 2013.
Huang, Q.: Retrospective investigation of geophysical data possibly associated with the M s8.0 Wenchuan earthquake in Sichuan, China, J. Asian Earth Sci., 41, 421–427, 2011.
Jonah, O. F., Kherani, E. A., and De Paula, E. R.: Investigations of conjugate MSTIDS over the Brazilian sector during daytime, J. Geophys. Res.-Space, 122, 9576–9587, 2017.
Klimenko, M. V., Klimenko, V. V., Karpov, I. V., and Zakharenkova, I. E.: Simulation of Seismo-Ionospheric Effects Initiated by Internal Gravity Waves, Russ. J. Phys. Chem. B, 5, 393–401, 2011.
Kong, J., Yao, Y., Zhou, C., Liu, Y., Zhai, C., Wang, Z., and Liu, L.: Tridimensional reconstruction of the Co-Seismic Ionospheric Disturbance around the time of 2015 Nepal earthquake, J. Geodesy, 3, 1–12, 2018.
Li, M. and Parrot, M.: Statistical analysis of the ionospheric ion density recorded by DEMETER in the epicenter areas of earthquakes as well as in their magnetically conjugate point area, Adv. Space Res., 61, 974–984, 2017.
Liu, J. Y., Le, H., Chen, Y. I., Chen, C. H., Liu, L., Wan, W., Su, Y. Z., Sun, Y. Y., Lin, C. H., and Chen, M. Q.: Observations and simulations of seismo-ionospheric GPS total electron content anomalies before the 12 January 2010 M7 Haiti earthquake, J. Geophys. Res., 116, A04302, https://doi.org/10.1029/2010JA015704, 2011.
Liu, J. Y., Chen, C. H., Sun, Y. Y., Chen, C. H., Tsai, H. F., Yen, H. Y., Chum, J., Lastovicka, J., Yang, Q. S., Chen, W. S., and Wen, S.: The vertical propagation of disturbances triggered by seismic waves of the 11 March 2011 M9.0 Tohoku earthquake over Taiwan, Geophys. Res. Lett., 43, 1759–1765, 2016.
Maruyama, T., Yusupov, K., and Akchurin, A.: Ionosonde tracking of infrasound wavefronts in the thermosphere launched by seismic waves after the 2010 M8.8 Chile earthquake, J. Geophys. Res.-Space, 121, 2683–2692, 2016.
Mikhailov, Y. M., Mikhailova, G. A., and Kapustina, O. V.: VLF effects in the outer ionosphere from the underground nuclear explosion on Novaya Zemlya island on 24 October, 1990 (INTERCOSMOS 24 satellite data), Phys. Chem. Earth Pt. C, 25, 93–96, 2000.
Otsuka, Y., Shiokawa, K., Ogawa, T., and Wilkinson, P.: Geomagnetic conjugate observations of equatorial airglow depletions, Geophys. Res. Lett., 29, 1753, https://doi.org/10.1029/2002GL015347, 2002.
Otsuka, Y., Shiokawa, K., Ogawa, T., and Wilkinson, P.: Geomagnetic conjugate observations of medium-scale traveling ionospheric disturbances at midlatitude using all-sky airglow imagers, Geophys. Res. Lett., 31, L15803, https://doi.org/10.1029/2004GL020262, 2004.
Park, J., Frese, R. R. B. von, Grejner-Brzezinska, D. A., Morton, Y., and Gaya-Pique, L. R.: Ionospheric detection of the 25 May 2009 North Korean underground nuclear test, Geophys. Res. Lett., 38, L22802, https://doi.org/10.1029/2011GL049430, 2011.
Park, J., Helmboldt, J., Grejner-Brzezinska, D. A., von Frese, R. R. B., and Wilson, T. L.: Ionospheric observations of underground nuclear explosions (UNE) using GPS and the Very Large Array, Radio Sci., 48, 463–469, 2013.
Pokhotelov, O. A., Pilipenko, V. A., Fedorov, E. N., Stenflo, L., and Shukla, P. K.: Induced electromagnetic turbulence in the ionosphere and the magnetosphere, Phys. Scripta, 50, 600–605, 1994.
Pokhotelov, O. A., Parrot, M., Fedorov, E. N., Pilipenko, V. A., Surkov, V. V., and Gladychev, V. A.: Response of the ionosphere to natural and man-made acoustic sources, Ann. Geophys., 13, 1197–1210, https://doi.org/10.1007/s00585-995-1197-2, 1995.
Pokhotelov, O. A., Pilipenko, V. A., and Parrot, M.: Strong atmospheric disturbances as a possible origin of inner zone particle diffusion, Ann. Geophys., 17, 526–532, https://doi.org/10.1007/s00585-999-0526-2, 1999.
Pulinets, S. A., Boyarchuk, K. A., Hegai, V. V., Kim, V. P., and Lomonosov, A. M.: Quasi-electrostatic model of atmosphere-thermosphere-ionosphere coupling, Adv. Space Res., 26, 1209–1218, 2000.
Ritter, P., Lühr, H., and Rauberg, J.: Determining field-aligned currents with the Swarm constellation mission, Earth Planets Space, 65, 1285–1294, 2013.
Ruzhin, Y. Y., Larkina, V. I., and Depueva, A. K.: Earthquake precursors in magnetically conjugated ionosphere regions, Adv. Space Res., 21, 525–528, 1998.
Sorokin, V. M., Chmyrev, V. M., and Yaschenko, A. K.: Electrodynamic model of the lower atmosphere and the ionosphere coupling, J. Atmos. Sol. Terr. Phy., 63, 1681–1691, 2001.
Xu, T., Hu, Y., Wu, J., Wu, Z., Li, C., Xu, Z., and Suo, Y.: Anomalous enhancement of electric field derived from ionosonde data before the great Wenchuan earthquake, Adv. Space Res., 47, 1001–1005, 2011.
Yang, Y.-M., Garrison, J. L., and Lee, S. C.: Ionospheric disturbances observed coincident with the 2006 and 2009 North Korean underground nuclear tests, Geophys. Res. Lett., 39, L02103, https://doi.org/10.1029/2011GL050428, 2012.
Zhao, B. and Hao, Y.: Ionospheric and geomagnetic disturbances caused by the 2008 Wenchuan earthquake: A revisit, J. Geophys. Res.-Space, 120, 5758–5777, 2015.
Zhang, X., Shen, X., Liu, J., Ouyang, X., Qian, J., and Zhao, S.: Analysis of ionospheric plasma perturbations before Wenchuan earthquake, Nat. Hazards Earth Syst. Sci., 9, 1259–1266, https://doi.org/10.5194/nhess-9-1259-2009, 2009.
Zhang, X., Shen, X., Zhao, S., Yao, L., Ouyang, X., and Qian, J.: The characteristics of quasistatic electric field perturbations observed by DEMETER satellite before large earthquakes, J. Asian Earth Sci., 79, 42–52, 2014.
Zhou, C., Liu, Y., Zhao, S., Liu, J., Zhang, X., Huang, J., Shen, X., Ni, B., and Zhao, Z.: An electric field penetration model for seismo-ionospheric research, Adv. Space Res., 60, 2217–2232, 2017.





