the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Investigation of the relationship between the spatial gradient of total electron content (TEC) between two nearby stations and the occurrence of ionospheric irregularities
Teshome Dugassa
John Bosco Habarulema
Melessew Nigussie
The relation between the occurrence of ionospheric irregularities and the spatial gradient of total electron content (TEC) derived from two closely located stations (ASAB: 4.34∘ N, 114.39∘ E and DEBK: 3.71∘ N, 109.34∘ E, geomagnetic), located within the equatorial region, over Ethiopia, during the postsunset hours was investigated. In this study, the Global Positioning System (GPS)-derived TEC during the year 2014 obtained from the two stations were employed to investigate the relationship between the gradient of TEC and occurrence of ionospheric irregularities. The spatial gradient of TEC (ΔTEC∕Δlong) and its standard deviation over 15 min, σ(ΔTEC∕Δlong), were used in this study. The rate of change of TEC-derived indices (ROTI, ROTIave) were also utilized. Our results revealed that most of the maximum enhancement and reduction values in ΔTEC∕Δlong are noticeable during the time period between 19:00 and 24:00 LT. In some cases, the peak values in the spatial gradient of TEC are also observed during daytime and postmidnight hours. The intensity level of σ(ΔTEC∕Δlong) observed after postsunset show similar trends with ROTIave, and was stronger (weaker) during equinoctial (solstice) months. The observed enhancement of σ(ΔTEC∕Δlong) in the equinoctial season shows an equinoctial asymmetry where the March equinox was greater than the September equinox. During the postsunset period, the relation between the spatial gradient of TEC obtained from two closely located Global Navigation Satellite System (GNSS) receivers and the equatorial electric field (EEF) was observed. The variation in the gradient of TEC and ROTIave observed during the evening time period show similar trends with EEF with a delay of about 1–2 h between them. The relationship between σ(ΔTEC∕Δlong) and ROTIave correlate linearly with correlation coefficient of C=0.7975 and C=0.7915 over ASAB and DEBK, respectively. The majority of the maximum enhancement and reduction in the spatial gradient of TEC observed during the evening time period may be associated with ionospheric irregularities or equatorial plasma bubbles. In addition to latitudinal gradients, the longitudinal gradient of TEC has contributed significantly to the TEC fluctuations.
The ionosphere, which consists of free electrons and ions, frequently experiences irregular electron density. After sunset, the ionospheric plasma interchange instabilities present in the equatorial–low-latitude ionosphere generate large-scale depletions in the ambient electron density, which leads to the formation of plasma density irregularities that affect radio communication and navigation systems (Basu and Basu, 1981). The generation of the plasma irregularities can be related to the decrease in plasma production immediately after sunset and the fast recombination rate in the E-region ionosphere, which results in a steep electron density gradient. The large enhancement of F-region vertical plasma drift in the evening hours due to the presence of enhanced eastward electric field is a critical driver which controls the generation of plasma density irregularities (Fejer, 1991; Fejer et al., 2008). This prereversal enhancement (PRE) vertical plasma drift moves the F region to higher altitudes (Abdu et al., 2009). When the altitude of F region is high enough to overcome recombination effects, the Rayleigh–Taylor (R-T) instability mechanism initiates growth in plasma fluctuations. The R-T instability is considered primarily responsible for the generation of ionospheric plasma density irregularities or plasma bubbles in the equatorial and low-latitude region (Rao et al., 2006a; Fejer et al., 1999). Kelley (2009) reported that the existence of equatorial plasma bubbles (EPBs) is attributed to the instability of the R-T plasma which is triggered by the intensification of the eastward equatorial electric field just before its reversal. The characteristics of ionospheric scintillation and ionospheric irregularities over the equatorial and low-latitude region in different longitudinal sectors during different solar and geomagnetic activities have been studied (e.g., Burke et al., 2004; Paznukhov et al., 2012; Oladipo and Schuler, 2013a; Seba and Tsegaye, 2015). Various instruments such as all-sky imagers (Wiens et al., 2006) and very high-frequency radar (e.g., Otsuka and Ogawa, 2009; Ajith et al., 2016) have been used to study the behavior of ionospheric irregularities and related scintillations. Recently, Global Navigation Satellite System (GNSS) signal analysis is an important tool to study the behavior of ionospheric irregularities (e.g., Pi et al., 1997; Nishioka et al., 2008; Watthanasangmechai et al., 2016; Magdaleno et al., 2017) because of its growing application in civilian and military applications.
The inhomogeneity of ionospheric electron distribution can cause sudden, rapid and irregular fluctuations of the amplitude and phase of the received signals, known as ionospheric scintillation (Wernik and Liu, 1974). This inhomogeneity, i.e, the spatial plasma density or TEC gradient, varies significantly in the low-latitude region because of geomagnetic storms, equatorial spread F (ESF) and the Appleton anomaly. As the GNSS signals pass through the ionosphere, the ionospheric irregularities also cause the delay of signals. The classification of the spatial electron density or TEC gradients can be given as latitudinal (north–south) and longitudinal (east–west) (Jakowski et al., 2004). It is normally found that the spatial plasma density gradients can be represented by means of TEC changes per latitude or longitude (TECU deg−1) or by their changes in distance (TECU km−1). In addition to threatening the of life-safety applications to air traffic management (Luo et al., 2002; Lee et al., 2011; Rungraengwajiake et al., 2015), the ionospheric TEC gradient is also unfavorable in terms of the communication and surveillance systems which depend on trans-ionospheric signal propagation (Foster, 2000). Radicella et al. (2004) and Nava et al. (2007) also presented the contribution of the horizontal gradients of vertical TEC to positioning error. The characteristics of horizontal ionospheric density gradients and their effects on trans-ionospheric radio wave propagation have been studied at different latitudes (Jakowski et al., 2005; Radicella et al., 2004). It has been reported that the majority of large or steep TEC gradients are associated with equatorial plasma bubbles (Pradipta and Doherty, 2016). Rao et al. (2006a) estimated ionospheric spatial gradient from F-region peak electron density (NmF2) data using a chain of radio soundings. Based on the GNSS data acquired by the dense distribution of receivers over the Brazilian longitude sector, Cesaroni et al. (2015) highlight the relationship between intensity and variability of TEC gradients and the occurrence of ionospheric scintillation.
Previous studies have attempted to explain the relationship between the latitudinal (north–south) gradient of TEC surrounding the anomaly region and ionospheric scintillation over different sectors (Mendillo et al., 2001; Valladares et al., 2001; Rao et al., 2006b; Ray et al., 2006; Muella et al., 2008). Mendillo et al. (2001) pointed out that equatorial ionization anomaly (EIA) strength at sunset is the best available precursor for premidnight ESF. Using latitudinal distribution of TEC measurements at about 20:00 LT, Valladares et al. (2001) observed a high crest-to-trough ratio prevalent to ESF days. Recently, Seba et al. (2018) investigated the relationship between equatorial ionization anomaly and nighttime ESF over the East Africa longitudinal sector using data from ground-based Global Positioning System (GPS) stations and a horizontal meridional neutral wind model. To identify signals which suffer severely from the ionospheric gradient, Ravi Chandra et al. (2009) and Rungraengwajiake et al. (2015) used rate of change of TEC (ROT) and rate of change of TEC index (ROTI). From the definition, however, ROTI mixes both the spatial and temporal gradients of TEC variations. To show the relation between EIA and ESF, Seba et al. (2018) used ROTI and the crest-to-trough ratio. Even though the characteristics of ionospheric irregularities and plasma bubbles over equatorial–low-latitude region of Africa under different solar and geomagnetic activities was discussed (Seba and Tsegaye, 2015; Seba and Nigussie, 2016; Mungufeni et al., 2016; Kassa and Damtie, 2017; Olwendo et al., 2018; Bolaji et al., 2019; Dugassa et al., 2019), a limited number of studies have been carried out over the region on the relationship between TEC gradient and the occurrence of ionospheric irregularities.
Gradient of electron density is one of the candidates which affects the growth rate of the R-T instability and hence the generation of ionospheric irregularities (Sultan, 1996). The magnitude of Pederson conductivity which can be estimated using electron density also has an effect on the growth rate. Over the African region, however, there is a lack of instrumentation (radar, ionosondes and/or incoherent scatter) to directly measure the gradient of electron density and investigate its relationship with the occurrence of ionospheric irregularities. It is generally known that TEC is the integral of electron density, and the spatial gradient of TEC between close-by stations would help us to examine its relation with ionospheric irregularity at those stations. Investigating the relationship between the spatial gradient of TEC and the occurrence of ionospheric irregularity using ground GPS-TEC receivers from two closely located stations is the aim of the current study. In this work, closely located GPS stations will also help to study the relationship between the gradient of TEC and electric field after sunset. The relation between the daytime eastward equatorial electric field derived from the equatorial electric field (EEF) model and the daytime equatorial electrojet (EEJ) obtained from ground-based magnetometer measurements was also discussed. The study is the first of its kind in the African sector to present the relation between the spatial gradient of TEC and the occurrence of ionospheric irregularities. The gradients of plasma density might be considered as an important parameter in the modeling of ionospheric irregularities and mitigating positioning errors on GNSS-based applications.
The GNSS data used for this study were obtained from the University NAVSTAR Consortium (UNAVCO) database (https://www.unavco.org/, last access: 8 December 2018). We used data from two receiver stations located in the East African region at Debark (geographic latitude 13∘ N, geographic longitude 37.65∘ E, geomagnetic latitude 4.13∘ N) and Asab (geographic latitude 13∘ N, geographic longitude 42.65∘ E, geomagnetic latitude 4.85∘ N) for the period 2014. The Receiver IndependentExchange (RINEX) observation files obtained from the IGS website were processed by the GPS-TEC application software developed at Boston College (Seemala and Valladares, 2011). The TEC analysis software uses the phase and code values for both L1 and L2 GPS frequencies to eliminate the effect of clock errors and tropospheric water vapor to calculate relative values of slant TEC (Sardón and Zarraoa, 1997; Arikan et al., 2008). In order to avoid the multipath effects, different authors have used observation data above certain cutoff masks ranging from 15 to 35∘ (Chu et al., 2005; Mushini and Pokhotelov, 2011). In the current study, an elevation cutoff mask of 30∘ was used for all the VTEC computed. Table 1 gives the list of all the stations for which data have been used in this study.
There are two independent ways of estimating the TEC gradient values using ground-based GPS receiver data (e.g., Lee et al., 2007, 2010). The first method uses a pair of closely spaced receiver stations, looking at the same GPS satellite to calculate the difference in TEC values between the two neighboring ionospheric piercing points at any given time. The second method uses a single GPS receiver station to infer the spatial TEC gradient values based on the observed temporal rate of change in TEC. In the current study, we have applied the first method to obtain the spatial gradient of TEC. Using the computed VTEC determined from the two receiver stations, the spatial gradient of TEC (difference of TEC between two stations per longitudinal separation) was computed for every time and then we analyzed its diurnal, monthly and seasonal variations. The two stations are located nearly along the same geographic latitude with longitudinal separation of about ∼5∘ or corresponding spatial separation of 535.7 km. Stations with the same latitude were selected to examine only the contribution of the longitudinal gradient of TEC to the generation of ionospheric irregularities expressed by ROTI. In the competition of the spatial gradient of TEC, the 1 min VTEC values for all satellites in view were averaged. The spatial gradient of TEC utilized in this study was computed using Eq. (1) (Lee et al., 2007; Ravi Chandra et al., 2009; Cesaroni et al., 2015).
where i=1 to 1440, and Δlong represents the difference in the longitude between the two stations. To detect the presence of plasma density irregularities, using ground and space-based TEC and plasma density measurements different authors presented different techniques. For example, Pi et al. (1997) applied the standard deviation of ROT over 5 min to characterize the occurrence of ionospheric irregularities. For in situ electron density measurements, Su et al. (2006) and Huang (2018) used the standard deviation of ion density variations over 10 s as indicator of ESF occurrence. Cesaroni et al. (2015) used the standard deviation of gradient of TEC to indicate the variability of the gradients. In this study, we used the standard deviation of the spatial gradient of TEC over 15 min, σ(ΔTEC∕Δlong), to examine the relationship between spatial gradient (zonal or east–west gradients) of TEC and occurrence of ionospheric irregularities.
The time variation of TEC, also known as rate of change of TEC (ROT and ROTI), which is a measure of large-scale ionospheric irregularities (Aarons et al., 1997), was used in this study. These indices are a good proxy for the phase fluctuation, and can be used to characterize all the known features of ESF (Mendillo et al., 2000). The ROT is given by
where i is the visible satellite and k is the time of epoch and ROT is in units of TECU min−1. The ROTI is defined as the standard deviation of ROT over a 5 min period and is mathematically given by Eq. (3) (Pi et al., 1997; Bhattacharyya et al., 2000; Nishioka et al., 2008). Usually, ROTI > 0.5 TECU min−1 indicates the presence of ionospheric irregularities at scale lengths of a few kilometers (Ma and Maruyama, 2006).
Oladipo and Schuler (2013b) employed the idea of Mendillo et al. (2000) to obtain a new index called the ROTIave index, given in Eq. (4). The ROTIave index is the average of ROTI over a 30 min interval for a satellite which is then averaged over all satellites in view. The index gives the average level of irregularities over half an hour. Recently, ROTIave has been applied to demonstrate and explain the level of ionospheric irregularities over the equatorial–low-latitude region of Africa (Oladipo et al., 2014; Bolaji et al., 2019; Dugassa et al., 2019). In this study, the rate of TEC fluctuation index (ROTI) and ROTIave (Pi et al., 1997; Oladipo and Schuler, 2013b; Oladipo et al., 2014) were used to observe the occurrence of ionospheric irregularities.
where n is the satellite number, 0.5 h is half an hour (0, 0.5, 1, …23.5, 24 h), i is the 5 min section within half an hour (i=1, 2, 3, 4, 5, 6), N is the number of satellites observed within half an hour and k is the number of ROTI values available within half an hour for a particular satellite. According to Oladipo and Schuler (2013b), the value of ROTIave<0.4, and ROTIave>0.8, respectively represents the background fluctuation, existence of phase fluctuation, and severe phase fluctuation activities. These threshold values were used to observe the relation between the occurrence of ionospheric irregularities and the spatial gradient of TEC.
The magnetic data used in this study are obtained from International Real-Time Magnetic Observatory Network (INTERMAGNET) and Africa-Meridian B-field Education and Research (AMBER) magnetometers installed in Addis Ababa (AAE, 9.0∘ N, 38.8∘ E, 0.2∘ N, geomagnetic) and Adigrat (ETHI, 14.3∘ N, 39.5∘ E, 6.0∘ N, geomagnetic), respectively. Both of the instruments provide 1 min values of the northward (X), eastward (Y) and vertical (Z) components of the Earth's magnetic field, from where the horizontal component (H) is computed using Eq. (5).
To avoid different offset values of different magnetometers, the nighttime baseline values in the H component (Eq. 6) are first obtained for each day and subtracted from the corresponding magnetometer data sets to obtain the hourly departure of H, denoted as δH and expressed by Eq. (7). The baseline value was defined as the average of the H-component nighttime (23:00–02:00 LT) value of the Earth's magnetic field.
where H23, H24, H01 and H02 are respectively the hourly values of H at 23:00, 24:00, 01:00 and 02:00 in local time (LT).
where t is the time in hours ranging from 01:00 to 24:00 LT. The hourly departure δH is then corrected for the noncyclic variation using (Eq. 8). This correction was proposed previously by Rastogi et al. (2004), who defined noncyclic variation as a phenomenon in which the value at 01:00 LT is different from that of local midnight (24:00 LT).
The hourly departure of H (δH) corrected for the noncyclic variation corresponding to the magnetometer data set gives the solar quiet variation (Sq) values as shown in Eq. (9):
where t=1 to 1440.
The EEJ produces a strong enhancement in the H-component magnetic field measured by magnetometers located within ±5∘ of the magnetic equator. Measurements of this magnetic field perturbation in equatorial magnetometers could provide a direct measure of the daytime EEJ and have strong relationships with dayside vertical velocity (E×B drift) (Anderson et al., 2004, 2006; Yizengaw et al., 2012). The equatorial stations respond primarily to the EEJ and also to the ring current and the global quiet time Sq current system. However, ground magnetometers just outside the extent of the EEJ (∼6–9∘, off the dip equator) exhibit an exact response to the ring and Sq currents, but near-zero response to the EEJ. To obtain the contribution of the H-component field to the EEJ current, we subtract the H-component value recorded off the equator (∼6–9∘ geomagnetic) from the H-component value measured at the magnetic equator, using Eq. (10). The subtraction has been made to remove the contribution of the ring current and global Sq dynamo from the H component.
where δHAAE and δHETHI, respectively, show the hourly departure of H over Addis Ababa and Adigrat.
The other data source used in this study is the Real-time model of the Ionospheric Electric Fields (http://geomag.org/models/PPEFM/RealtimeEF.html, last access: 27 May 2018). The Prompt Penetration Electric Field Model (PPEFM) (Manoj and Maus, 2012) is a transfer function model which models the daily variations coming from the solar wind, which are mapped in the interplanetary electric field (IEF) data. Eight years of IEF data from the ACE satellite, radar data from Jicamarca Unattended Long-Term studies of the Ionosphere and Atmosphere (JULIA) system, and magnetometer data from the CHAMP satellite have been used to derive the transfer function. By using the real-time data from the ACE satellite, the transfer function models the current variations in the equatorial ionosphere. To calculate the best estimates of the equatorial electric field, the model takes time and location as input parameters. The model outputs provide the electric field generated as a result of the convective electric field, quiet time electric field and both of these. In the present study, we have used the background quiet-time electric field to examine the relation between the EEF and the spatial gradient of TEC derived from the two nearby stations. To have a rough idea about the PPEFs during storm days, we have also used the quiet-time and penetration electric field.
The real-time model of electric field has been used for different case studies over different sectors to observe the influence of the prompt penetration electric field (PPEF) on the variations of total electron content and the occurrence of ionospheric irregularities (Nayak et al., 2017; Dugassa et al., 2019). However, this model has not been applied yet to explain the electrodynamic phenomena over the African low-latitude region. To use the PPEF model in this region, we presented its relationship with EEJ, an indicator of the eastward electric field, during the daytime period over the equatorial region of Africa based on ground-based magnetometer measurements (Rastogi and Klobuchar, 1990; Anderson et al., 2002; Yizengaw et al., 2014). It has been reported that the strength of EEJ before sunset has a correlation with the generation of ESF during the nighttime period preceded by a rise in the F region (Dabas et al., 2003; Uemoto et al., 2010; Tulasi Ram et al., 2007). The relation between the EEF obtained from the real-time electric field model and ΔH was determined. The EEF derived from the real-time electric field model was used in this study to explain the influence of the equatorial electric field on nighttime variations of the spatial gradient of TEC and the occurrence of ionospheric irregularities. The temporal resolution of EEF was 5 min and that of ΔH was 1 min. To make their resolution consistent, the 5 min averages of ΔH of each of the selected quiet days were computed. In this study, ΔH derived from the H component of the geomagnetic field of the two stations during quiet days of the year 2012 was used. In this year, we have a large number of magnetometer measurements relative to other years. From each month of the year 2012, the 5 quiet international days (total of 38) obtained from http://wdc.kugi.kyoto-u.ac.jp/qddays/index.html (last access: 8 December 2018) were selected to show the correlation between ΔH and EEF. Since the EEJ is a daytime phenomenon, only the daytime values of EEF and ΔH during (07:00 to 17:00 LT) were examined.
3.1 Relation between the daytime equatorial electrojet (EEJ) and equatorial electric field (EEF) model
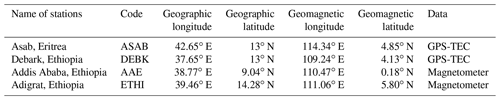
Figure 1a presents the diurnal variation of the EEF and EEJ current signature of the H component of the geomagnetic field on 26 March 2012. As can be seen in Fig. 1a, during the daytime period (07:00–17:00 LT), ΔH and EEF show similar trends. The relationship between the strength of daytime EEJ derived from ΔH and EEF obtained from the equatorial electric field model is shown in Fig. 1b. To show the performance of the EEF model over the East African sector, we have presented the relationship between ΔH and EEF for 5 international quiet days of each month of the year 2012. As depicted in Fig. 1b, during the daytime period, the ΔH correlates positively and linearly with EEF with the correlation coefficient, C=0.60. Manju et al. (2012) obtained an excellent agreement with observations at the Indian and South American sectors. Different techniques have been utilized to estimate the ionospheric electric field (e.g., Hysell and Burcham, 2000; Anderson et al., 2002; Alken et al., 2013; Dubazane and Habarulema, 2018). Anderson et al. (2002) proposed ΔH deduced from ground-based magnetometers as a proxy of the equatorial electrojet current. They reported that the vertical plasma drifts observed from Jicamarca incoherent scatter radar (ISR) has a positive and linear relation with ΔH and henceforth ΔH was widely taken as a proxy substitute for the EEF. Anderson et al. (2006) and Yizengaw et al. (2011) also reported a strong relation between the dayside vertical velocity (E×B drift) and ΔH. Alken et al. (2013), on the other hand, estimates the EEF using CHAMP satellite-derived latitudinal current profiles of daytime EEJ along with ΔH measurements from ground magnetometer stations and they showed that pair of magnetometer stations, one located near the magnetic equator and the other off the equator, capture the day-to-day strength of the EEJ.
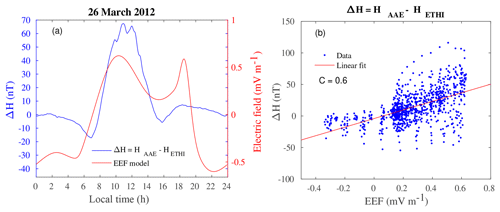
Figure 1(a) Example showing the diurnal variation of the equatorial electric field (EEF) model (red curve) and ΔH (blue curve) during 26 March 2012 and (b) The correlation between the equatorial electrojet (EEJ) and quiet-time EEF model during the daytime (07:00–17:00 LT) period for quiet days of the year 2012. The red line shows the linear fit of data points.
The daytime eastward equatorial electric field in the ionospheric E region plays an important role in equatorial ionospheric dynamics. It is responsible for driving the EEJ current system, equatorial vertical ion drifts and the equatorial ionization anomaly. The EEJ is a strong ionospheric current along the magnetic equator driven by the dayside eastward electric field. Studies also show that the daytime electrodynamics play a decisive role in the initiation of postsunset ESF (e.g., Mendillo et al., 2001; Valladares et al., 2001, 2004). The connection between the occurrence of ESF during the evening sector preceded by the rapid rise in the F layer and the strength of EEJ before sunset has been presented (Dabas et al., 2003; Burke et al., 2004; Kelley, 2009; Uemoto et al., 2010; Tulasi Ram et al., 2007). Sreeja et al. (2009) reported observational evidence for the plausible linkage between the daytime EEJ related electric field variations with the postsunset F-region electrodynamics. Furthermore, Hajra et al. (2012) indicate that the afternoon–evening time variation of the eastward electric field as revealed through EEJ seems to play a dominant role in dictating the postsunset resurgence of EIA and consequent generation of spread-F irregularities. Since the EEF-derived model correlate moderately with ΔH over the East Africa longitudinal sector, we could use the real-time EEF model over the equatorial–low-latitude region of Africa to explain some special features of ionospheric phenomena like plasma density irregularities and the positive/negative spatial gradient of TEC between the two stations.
3.2 Relation between the equatorial electric field (EEF), the spatial gradient of TEC and occurrence of ionospheric irregularity
Figure 2a–l shows the diurnal variation of the quiet-monthly mean of the spatial gradient of TEC (blue curves) and EEF (along ∼40∘ E) (red curves) in the year 2014. We superimpose EEF and the spatial gradient in TEC to observe the effect of EEF on the variability of the gradient in TEC and/or the occurrence of ionospheric irregularities. In the computation of the spatial gradient of TEC (using Eq. 1), negative and positive values in the gradient of TEC may be observed during the nighttime and daytime, respectively. Both the negative and positive differences of TEC between the two stations show the gradient of TEC. A positive (negative) gradient in TEC denotes an enhancement (reduction) in TEC or electron density over ASAB relative to DEBK. The gradient in TEC is positive when TEC over ASAB is greater and is negative when TEC over DEBK is greater. This difference may be attributed to different physical processes, like neutral winds and plasma drift. In this study, the terms maximum enhancement and reduction in the gradient of TEC (in terms of magnitude) were used when the nighttime value of gradient of TEC was larger than the daytime value. There were also cases of the gradient in TEC during the daytime being greater than nighttime values. It can be seen from Fig. 2 (red curves) that around evening hours, enhancement in EEF was observed in the equinoctial months and was relatively weak during the June and December solstices. It has been stated that an enhanced eastward electric field will be produced from the electrodynamical interaction of the eastward thermospheric wind with the geomagnetic field around the dip equator at the sunset terminator when longitudinal gradient conductivity exists between the high-conducting dayside ionosphere and the low-conducting nightside ionosphere (Batista et al., 1986; Heelis et al., 1974). Most of the enhancement and reduction in the TEC gradient was observed before midnight (19:00–24:00 LT) and after midnight (24:00–06:00 LT) but after 1–2 h of the postsunset enhancement of the equatorial electric field. During the nighttime period, the maximum enhancement and reduction in the spatial gradient of TEC were found mostly in the range between 5.0 and −5.0 TECU deg−1. A variation in the spatial gradient of TEC observed after midnight may be due to the plasma bubbles (Ratnam et al., 2018). In some days, the spatial gradient of TEC observed during the daytime was relatively small compared to the evening time hours. The maximum enhancement and reduction in the gradient of TEC and the peak in the EEF observed during the premidnight period were significant during the equinoctial months. After the postsunset period, the maximum enhancement and reduction in the gradient of TEC in solstice months were small compared to equinoctial months, when the PRE electric field observed in the evening period was minimum. Yoshihara et al. (2005) confirmed the larger ionospheric gradients during summer and followed by autumn. The ionospheric gradients are lower during winter as compared to summer and autumn. The enhancement and reduction in the gradient of TEC observed in the evening period could be related to the PRE in the zonal electric field.
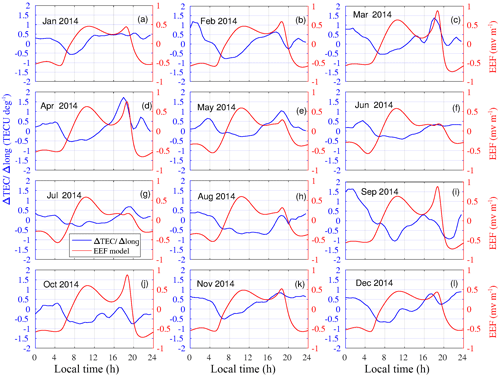
Figure 2Comparison of quiet-monthly mean of EEF derived from real-time electric field model at ∼40∘ E and spatial gradient of TEC between ASAB and DEBK in the year 2014.
Figure 3a–d shows the diurnal variation of the spatial gradient of TEC (blue curve) and ROTIave (red and black curves) over ASAB and DEBK stations. The ROTIave values in each panel were greater than 0.4 TECU min−1, a threshold value showing the presence of irregularities in the premidnight hours. Likewise, maximum enhancement and reduction in the gradient of TEC were observed during the premidnight and postmidnight periods, respectively. It is evident from Fig. 3 during the postsunset period that the pattern of ROTI (observed in both stations) and the spatial gradient in TEC show a kind of similar trend. Different researchers used the concept of ionosphere spatial gradient based on multi-GNSS observations within a small-scale region to provide corrections and integrity information to the Ground-Based Augmentation System (GBAS) (Rungraengwajiake et al., 2015; Saito and Yoshihara, 2017). They attribute the large ionosphere spatial gradient to the TEC enhancements and the ionosphere irregularities. Saito and Yoshihara (2017) associated the spatial gradient in ionospheric TEC with plasma bubbles. Rungraengwajiake et al. (2015) analyzed plasma bubbles at postsunset equinox time and observed the higher scales in east–west gradients compared with north–south gradients for the GBAS system, however, Cesaroni et al. (2015) reported that the north–south gradient in TEC correlates better with ionospheric scintillation than the east–west gradient of TEC. The plasma density variability, either the spatial and/or temporal, causes not only the GNSS-based positioning error but also radio wave scintillation.
The maximum enhancement and reduction in the gradient of TEC and the associated ionospheric irregularity during the postsunset period can be explained by ionospheric electrodynamics. It is well known that Earth's equatorial ionosphere presents temporal and spatial variations. The electrodynamics of the low-latitude ionosphere after sunset is influenced by the F-region dynamo, which is governed by a longitudinal gradient of the electrical conductivity and thermospheric zonal wind (Crain et al., 1993). Anderson et al. (2004) showed that the scintillation activity is related to the maximum E×B drift velocity between 18:30 and 19:00 LT. Mendillo et al. (2001) have pointed out that the best available precursor for the premidnight equatorial spread F (ESF) is the equatorial ionization anomaly (EIA) strength at sunset, which is in turn influenced by the magnitude of PRE. Using differential TEC profiles, TEC (at 18:00) − TEC (at 20:00), Valladares et al. (2004) explained that the PRE of the vertical drift would re-energize the fountain effect. The postsunset EIA produces a large plasma density gradient from the trough region to the crest region. Takahashi et al. (2016) observed the steepest TEC gradient with a difference of 30–50 TECU from the inside to outside plasma bubbles.
In the evening sectors, the vertical drift enhancement is of particular significance as it is the major driver for the generation of ESF (Farley et al., 1970; Woodman, 1970; Basu et al., 1996; Fejer et al., 1999; Martinis et al., 2005). Tulasi Ram et al. (2006) reported that the rapid postsunset enhancement of the zonal electric field leads to a large vertical plasma drift (E×B), thereby lifting the F layer to higher altitudes and resulting in a condition conducive for the generation of ESF. Ionospheric irregularities are mostly observed over the equatorial–low-latitude region 1–2 h after the PRE. Rastogi and Woodman (1978) showed that ESF can appear at any time of the night other than the postsunset period following the abnormal reversal of the vertical F-region drifts to an upward direction, with a delay of about 1–2 h. As illustrated in Fig. 2, the influence of postsunset enhancement in the zonal electric field on the maximum enhancement and reduction in the spatial gradient of TEC during the postsunset period can be seen. This could indicate maximum enhancement and reduction in the spatial gradient of TEC and the occurrence of ionospheric irregularities have some degree of relationship.
Figure 4a–h indicate representative cases showing the diurnal variation of ROTIave over ASAB (red curve) and DEBK (black curve) and σ(ΔTEC∕Δlong) (blue curve) during the occurrence of ionospheric irregularities (a–d) and during their absence (e–h). It is clearly observed from Fig. 4a–d that intensity level of ROTIave was greater than 0.4 TECU min−1, indicating the presence of ionospheric irregularities. Figure 4e–h on the other hand indicate examples when ionospheric irregularities are absent, where the value of ROTIave was less than 0.4 TECU min−1. ROTIave≥0.4 TECU min−1 indicates the presence of ionospheric irregularities (Oladipo and Schuler, 2013b; Oladipo et al., 2014). As can be seen from Fig. 4 (blue curves), the intensity level of σ(ΔTEC∕Δlong) observed in the evening period was higher when irregularities were present (Fig. 4a–d) than when irregularities were absent (Fig. 4e–h). It is evident from the figures that the strength of σ(ΔTEC∕Δlong) observed in the nighttime period was greater than the daytime value, as ROTIave does. The postsunset plasma bubble irregularities are generated at the bottom side of the F layer by the sunset enhancement of the zonal electric field, which is called prereversal enhancement and is caused by the combined action of an eastward thermospheric wind and the longitudinal gradient in ionospheric conductivity that exist along sunset terminator (Rishbeth, 1971; Fejer et al., 1999). It is well documented that plasma bubble development depends on the linear growth rate for the generalized R-T instability process, the flux tube integrated Pedersen conductivity that controls the nonlinear development, and density perturbations that are needed to act as a seed to trigger the instability growth. The PRE is generated through the interaction of zonal neutral wind in the F region and the conductivity gradient caused by the terminator. The density gradient affects the R-T instability growth rate and thus the generation of irregularities (Ossakow, 1981; Mendillo et al., 1992). Background electron density and its distribution in the ionosphere affects the formation of ionospheric irregularities. The intensity level of σ(ΔTEC∕Δlong) obtained from two closely located stations observed near the sunset terminator, related to the longitudinal gradient of ionospheric conductivity, could indicate the presence or absence of large-scale ionospheric irregularities. Cesaroni et al. (2015) reported a strong relationship between the standard deviation of the gradient of TEC and the occurrence of ionospheric scintillation.
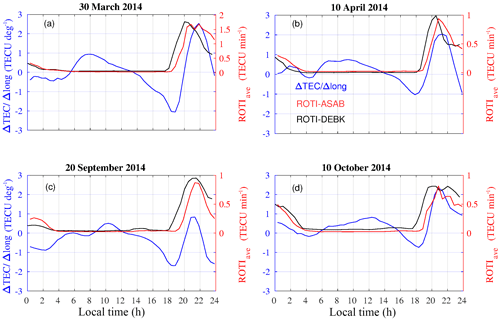
Figure 3Typical examples of diurnal variation in the spatial gradient of TEC (blue curve) and the ROTI over ASAB (red curve) and DEBK (black curves) on (a) 30 March 2014, (b) 10 April 2014, (c) 20 September 2014 and (d) 10 October 2014.
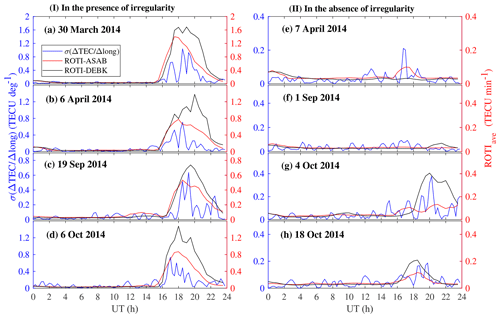
Figure 4Typical examples of the diurnal variation of σ(ΔTEC∕Δlong) (blue curve) and ROTIave over ASAB (red curve) and DEBK (black curves) (I) in the presence of ionospheric irregularities on (a) 30 March 2014, (b) 6 April 2014, (c) 19 September 2014 and (d) 6 October 2014 and (II) in the absence of ionospheric irregularities on (e) 7 April 2014, (f) 1 September 2014, (g) 4 October 2014 and (h) 18 October 2014. Local time (LT) = UT + 3 h.
Figure 5a–d illustrates typical examples of the diurnal variation of σ(ΔTEC∕Δlong) and ROTIave during some of selected geomagnetic storm periods. During the study period, days with the disturbance storm time index (Dst) nT (http://wdc.kugi.kyoto-u.ac.jp/, last access: 12 March 2019) were considered. To reflect the effect of storms (during the study period) on the variation of the ROTI and spatial gradient, four sample storm periods were selected: (a) 17–21 February 2014, (b) 10–14 April 2014, (c) 25–29 August 2014 and (d) 10–14 September 2014. These storm days are categorized as moderate (−100 nT ≤ Dst ≤ −50 nT) and strong magnetic storms (Dst ≤ −100 nT) (Loewe and Prölss, 1997; Echer et al., 2013). Figure 5iv, a–d and v, a–d respectively show the temporal variation of the Dst and z component of interplanetary magnetic field (IMF Bz) during the storm periods. The storm observed during 17–21 February was highly complex and had multiple main and recovery phases resulting from a series of Earth-directed coronal mass ejections (CMEs) (see Ghamry et al., 2016, for details). The intense storm of 17 February started with sudden storm commencement (SSC) at 09:00 UT. The storm event was characterized by a southward turning of IMF Bz with a magnitude of 13 nT and a depressed Dst index of minimum value −120 nT at 09:00 UT on 19 February, which was followed by the recovery phase on 21 February. The storm event during 10–14 April 2014 is moderate, with a maximum negative excursion of Dst nT at 10:00 UT on 12 April, corresponding to a negative (southern) IMF nT. On 12 April 2014, a change in polarity of the z component of IMF from southward to northward at ∼ 20:00 UT was observed. The maximum negative excursion of Dst nT at 19:00 UT and IMF nT at 15:00 UT was observed during storm event on 26–29 August 2014. During the 10–14 September 2014 storm period, however, minimum Dst of nT at 00:00 UT and IMF nT at 22:00 UT were observed. On 12 September 2014, the z component of IMF turned southward at about 20:00 UT.
To present the effect of the storms on the variation of ionospheric irregularities and spatial gradient of TEC, the quiet-monthly mean of ROTI and σ(ΔTEC∕Δlong) were used as a background condition (indicated by red curves) in Fig. 5a.i–iii–d.i–iii. The intensity level of ROTI and σ(ΔTEC∕Δlong) observed after the postsunset period during the storm main phase (on 19 February and 12 April 2014) (see Fig. 5a.i–iii and b.i–iii) was lower than the quiet-monthly mean, indicating the suppression effect of the storms on the occurrence of ionospheric irregularities. During the 12 September 2014 storm main phase, however, the intensity level of ROTI and σ(ΔTEC∕Δlong) observed after sunset was greater than the quiet-monthly mean, indicating the triggering effect. During the second storm main phase on 20 February 2014, the intensity level of both ROTI and σ(ΔTEC∕Δlong) was higher than the quiet-monthly mean values. During the storm main phase of 27 August 2014, on the other hand, a significant effect of the storm on the occurrence of ionospheric irregularities and spatial gradient was not observed.
When the presence of ionospheric irregularity is observed over both stations (ROTIave≥0.4 TECU min−1), the magnitude of σ(ΔTEC∕Δlong) observed in the postsunset period shows enhancement (for example, 12 September and 12 April 2014); and when the occurrence of ionospheric irregularities is suppressed (ROTIave<0.4 TECU min−1), the magnitude of σ(ΔTEC∕Δlong) shows reduction (for example, 19 February 2014). During storm days, when the presence of ionospheric irregularities is observed and suppressed, the spatial gradient of TEC TECU deg−1 and TECU deg−1 were observed, respectively. The magnitude of σ(ΔTEC∕Δlong) observed during nighttime periods could indicate the presence or absence of ionospheric irregularity. In the presence of ionospheric irregularities, the enhancement (reduction) in the spatial gradient of TEC observed during postsunset period during geomagnetically quiet (disturbed) conditions is higher than when ionospheric irregularities are suppressed (see Figs. 4 and 5). The triggering or suppression in the occurrence of ionospheric irregularities during geomagnetic storms was related to the enhancement or reduction in the gradient of TEC, σ(ΔTEC∕Δlong) (see Fig. 5). As can be seen from Fig. 5, the geomagnetic storm appears to show a similar effect on the spatial gradient of TEC as it has on ionospheric irregularities. The intensity level of both ROTI and σ(ΔTEC∕Δlong) observed during postsunset hours was affected by geomagnetic storms. The magnitude of the spatial gradient of TEC show enhancement and reduction during the 12 September and 19 February 2014 storm days, respectively. In the same way, the intensity level of ROTI (a proxy of ionospheric irregularities) during the storms was above and below the threshold value on 12 September and 19 February 2014, respectively.
The effect of geomagnetic storms on the occurrence of ionospheric irregularities could be related to the magnitude and polarity of the z component of IMF Bz (Biktash, 2004) or the local time at which the maximum negative excursion of Dst occurs (e.g., Aarons and DasGupta, 1984; Aarons, 1991). During magnetic disturbances when the IMF Bz is southward, the penetration of magnetospheric to low-latitude regions results in an eastward disturbance electric field on the dayside and westward electric field disturbance on the nightside, with the effect being a maximum in the dusk sector which augments with evening prereversal enhancement (Fejer and Scherliess, 1998). When the IMF Bz turns northward, however, the polarity of the low-latitude electric fields are reversed (Kelley et al., 1979). On 19 February 2014 (Fig. 5a.v) and 12 April 2014 (Fig. 5b.v), a northward turning of IMF Bz occurs around ∼ 15:00 and ∼ 19:00 UT, respectively. When the northward turning of IMF Bz occurs around dusk, the overshielding electric field might develop and cause a decrease in the upward vertical plasma drift and hence suppress the occurrence of ionospheric irregularities. Based on local time at which the maximum negative excursion of Dst occurs, Kassa and Damtie (2017) indicated the suppression effect of storm occurred on 19 February 2014 during the occurrence of ionospheric irregularities. In the case of 12 September 2014, however, a southward turning of IMF Bz occurs around dusk (∼ 19:00 UT). In this period of transient southward turning of IMF Bz, the undershielding electric field might cause eastward perturbation which reinforces the original PRE electric field, thus increasing the vertical plasma drift. This leads to the triggering effect of the storm on the occurrence of irregularities. The enhancement and reduction in the intensity level of the spatial gradient of TEC indicated by σ(ΔTEC∕Δlong) during the storm periods respond to the storm similarly to ROTI. During storm recovery phases (for example, 13–14 April and 13–14 September 2014), the triggering/suppression in the occurrence of ionospheric irregularities also appears to be related to enhancement and reduction in the gradient of TEC.
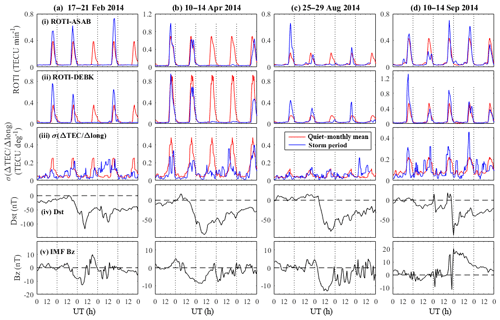
Figure 5Variation of ROTI over (i) ASAB and (ii) DEBK, and (iii) σ(ΔTEC∕Δlong) during geomagnetic storms (blue curves): (a) 17–21 February 2014, (b) 10–14 April 2014, (c) 26–29 August 2014 and (d) 10–14 September 2014 with respect to the quiet-monthly mean (red curves). Local time (LT) = UT + 3 h.
Geomagnetic storms were reported to either trigger or inhibit the occurrence of ionospheric irregularities (Aarons, 1991; Martinis et al., 2005; Oladipo and Schuler, 2013a; Kassa and Damtie, 2017). Different suggestions have been reported on how the geomagnetic storm affects the PRE electric field and hence the generation of ionospheric irregularities (e.g., Aarons, 1991; Biktash, 2004). During geomagnetic storms, the PPEF and the disturbance dynamo electric field (DDEF) are the two major electric field sources which change the magnitude or polarity of the background electric field. The PPEF direction is eastward (westward) during daytime (nighttime), whereas the DDEF has opposite polarity to the PRE electric field and PPEF. They affect the occurrence of ionospheric irregularities by modulating the background electric field. In the absence of observations over the region of interest, the PPEFM (Manoj and Maus, 2012) can be utilized to observe the effect of PPEFs. To indicate the mechanism that affects the occurrence of ionospheric irregularities, we presented the temporal variation of the equatorial electric field over 37∘ E under geomagnetic storm conditions for (a) 19 February 2014, (b) 12 April 2014, (c) 27 August 2014 and (d) 12 September 2014 (see Fig. 6). The blue curve represents the background quiet-time electric field. The red curve represents the total electric field (PPEF superimposed on the background quiet-time electric field). On 19 February 2014 (Fig. 6a), it can be clearly noted that the total electric field observed near sunset (∼ 18:00 LT, indicated by black arrow) is below the background electric field. It must be mentioned here that the reduced PRE may have contributions from westward disturbance dynamo (DDEF) electric field. On this storm day, in addition, the Bz component of the interplanetary magnetic field during dusk turns northward, related to the overshielding electric field which suppresses the background electric field. As a result, the postsunset ionosphere drifts downward, leading to the suppression in the ionospheric irregularities (represented by ROTI) and reduction in the spatial gradient of TEC (represented by σ(ΔTEC∕Δlong)) relative to quiet background conditions. The inhibition (triggering) effect of 12 April 2014 (12 September 2014) storm events on the occurrence of ionospheric irregularities and spatial gradient was not evident from storm-time EEF. This could be due to differences in the intensity of the storm. While the storm on 19 February 2014 is strong (Dst = −120 nT), it is moderate during the other events (−87, −79 and −88 nT) on 12 April, 26 August and 12 September 2014, respectively. In addition, the mechanism can be explained by the local time at which the maximum negative excursion of the ring current energy occurs (Aarons and DasGupta, 1984; Aarons, 1991). During the 12 April and 12 September 2014 storm main phases, the peak negative excursion of Dst occurs around the daytime and postmidnight periods, respectively. The occurrence of ionospheric irregularity observed was inhibited and triggered, consistent with Aarons (1991), and the spatial gradient of TEC, too. The triggering and inhibition effect of the storm on the generation of ionospheric irregularities could also be related to the magnitude and direction of the z component of the interplanetary magnetic field (Biktash, 2004). It is evident from Figs. 4 and 5 that the spatial gradient of TEC, σ(ΔTEC∕Δlong), obtained from two closely located stations could show the presence and absence of ionospheric irregularities.
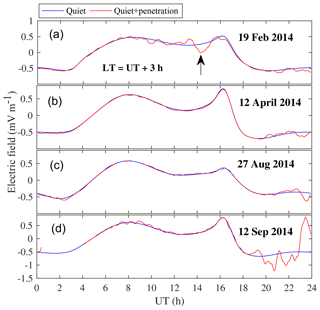
Figure 6Prompt penetration electric field observed during storm days of (a) 19 February 2014, (b) 12 April 2014, (c) 27 August 2014 and (d) 12 September 2014. The arrow indicates time of PRE. Local time (LT) = UT + 3 h.
Figure 7a–d respectively show the annual variation of ROTIave over ASAB and DEBK, the spatial gradient of TEC (ΔTEC∕Δlong) and its standard deviation σ(ΔTEC∕Δlong) in the year 2014. The intensity level of ROTIave, ΔTEC∕Δlong, and σ(ΔTEC∕Δlong) is indicated in the color bar. As stated by Oladipo and Schuler (2013b), the value of ROTIave≥0.4 TECU min−1 shows the presence of ionospheric irregularity. The occurrence of ionospheric irregularities at the two stations, as indicated by the intensity level of ROTIave, was predominantly observed in the premidnight periods, mainly between 19:00 and 24:00 LT. The large-scale ionospheric irregularities, which are responsible for the scintillation of trans-ionospheric signals at GNSS frequencies, are more pronounced during postsunset hours. The observed phase fluctuation shows monthly variations and there is also a seasonal trend in the occurrence of ionospheric irregularity. Strong and weak ionospheric irregularities are observed in the March equinox and in June–July solstices, respectively.
It can be seen from Fig. 7c that positive and negative values in the gradient of TEC were observed. Maximum enhancement and reduction in the gradient of TEC was observed mostly during the postsunset (18:00–24:00 LT) and postmidnight (24:00–06:00 LT) periods, respectively. Equation (1) was applied to all days (364 d) of the year 2014 in computing the spatial gradient of TEC. Out of the total observed daily maximum value of the gradient of TEC, about 194 d (about 53 %) fall in this time period. There were also cases where the maximum enhancement and reduction in the values of the gradient of TEC were observed in the early morning period. In Fig. 7d the diurnal, monthly and seasonal variation in the standard deviation of the spatial gradient of TEC, σ(ΔTEC∕Δlong), was clearly observed, and its variation shows similarity with variation in ROTIave. Maximum enhancement in σ(ΔTEC∕Δlong) was observed in the evening time period, 19:00–24:00 LT. The seasonal variation in σ(ΔTEC∕Δlong) also appears frequently in equinoctial months, but rarely in solstice months. Such variation could be related to the magnitude of E×B drift. Cesaroni et al. (2015) also found a seasonal variation of the TEC spatial gradients and they reported that it is larger during the equinoctial seasons than in the solstice seasons.
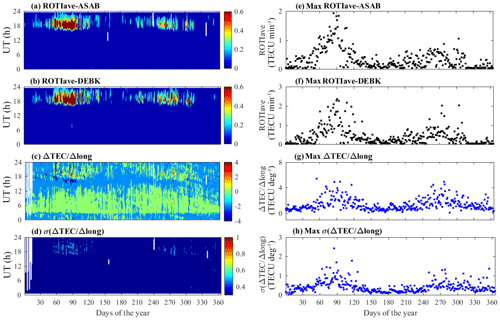
Figure 7Annual and daily maximum value variation of (a, b) ROTIave over Asab (ASAB), (c, d) ROTIave over Debark (DEBK), (e, f) spatial gradient of TEC (ΔTEC∕Δlong), (g, h) standard deviation of gradient of TEC σ(ΔTEC∕Δlong) in the year 2014. The ROTIave in TECU min−1 and ΔTEC∕Δlong in TECU deg−1 is indicated in color bar. Local time (LT) = UT + 3 h.
Figure 7e–h show the daily maximum values of ROTIave over ASAB and DEBK, spatial gradient of TEC (ΔTEC∕Δlong), and standard deviation of spatial gradient of TEC σ(ΔTEC∕Δlong), respectively, in the year 2014. As can be observed from Fig. 7e–h, the daily maximum value of ROTIave, ΔTEC∕Δlong and σ(ΔTEC∕Δlong) shows monthly and seasonal variations, and an equinoctial asymmetry is also observed. The daily maximum value of ΔTEC∕Δlong and σ(ΔTEC∕Δlong) shows similar trends with the daily maximum value of ROTIave observed over ASAB and DEBK stations. The trend they show has similarity with the time of occurrence of maximum enhancement and reduction as well as monthly and seasonal variations. Moreover, the seasonal variation observed in both variables exhibits equinoctial asymmetry, where the March equinox was greater than September equinoxes. The mechanism of generation of the enhancement in vertical drift just after sunset was detailed by Farley et al. (1986). The magnitude of peak vertical drift is known to control the seasonal and day-to-day variations in the occurrence of equatorial spread F (Manju et al., 2009; Tulasi Ram et al., 2006).
Figure 8 depicts the quiet-monthly mean of ROTIave (over ASAB and DEBK: red and black curves) and σ(ΔTEC∕Δlong) (blue curve) in the year 2014. The enhancement (reduction) in the intensity of σ(ΔTEC∕Δlong) shows similar trends with ROTIave and was stronger (weaker) during equinoctial (solstice) months. Equinoctial asymmetry both in ROTIave and σ(ΔTEC∕Δlong) was also evident from Fig. 8, where March equinoxes were stronger than September equinoxes. As expected, the TEC spatial gradients are also found to be larger during the equinoctial seasons than in the solstice seasons.
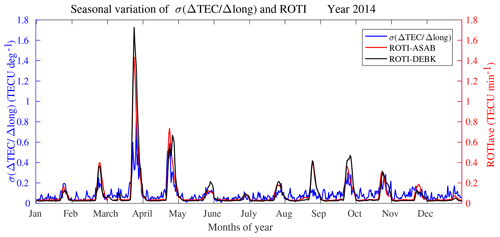
Figure 8Seasonal variation of ROTIave over ASAB (red curve), ROTIave over DEBK (black curve) and σ(ΔTEC∕Δlong) (blue curve) in the year 2014.
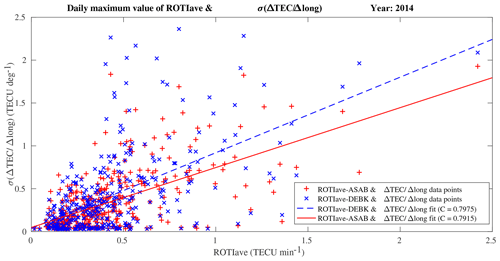
Figure 9Relation between the daily maximum value of σ(ΔTEC∕Δlong) and the daily maximum value of ROTIave over ASAB (red, +) and DEBK (blue, ×) in the year 2014. The blue broken and solid red lines indicate the linear fit between the daily maximum value of σ(ΔTEC∕Δlong) and ROTIave for ASAB and DEBK, respectively.
Figure 9 shows the relationship between the standard deviation of the spatial gradient of TEC σ(ΔTEC∕Δlong) and ROTIave (over ASAB and DEBK) in the year 2014. The daily maximum values of σ(ΔTEC∕Δlong) and ROTIave were considered to examine the correlation. The correlation coefficient between σ(ΔTEC∕Δlong) and ROTIave is about 0.7915 (in ASAB) and 0.7975 (in DEBK), respectively. Studies indicate that the gradient of TEC can be computed from a pair of closely spaced receiver stations (<2∘) such that the two receivers share the same GPS satellite. In our case, however, the two stations are separated by 5∘. The moderate correlation obtained might be attributed to the wider longitudinal separation (5∘) between the two stations. The other factor for the moderate correlation between the gradient of TEC and the occurrence of ionospheric irregularities might be the way ROTI was computed (since ROTI contains both the spatial and temporal variation in TEC). It is well known that ROT is the combination of the spatial and temporal gradients. However, by giving less attention to the spatial gradient effect, previous authors often used ΔTEC∕Δt to examine the fluctuation in TEC. It is not only the temporal variation of TEC that contributes to the fluctuation in the phase and amplitude of the signals but also the spatial gradient of TEC. The computed correlation coefficient between the TEC gradient and ROTI, here, gives an indication of the contribution of the spatial gradient of TEC to ROTI (or ROT) usage. This can give the case where the spatial gradient of TEC between two closely located stations can be used as an indicator of the occurrence of ionospheric irregularities. Every nighttime enhancement (reduction) in the gradient of TEC may not be a guarantee to indicate the occurrence (nonoccurrence) of ionospheric irregularities. However, there are cases which show the occurrence of irregularities over both stations (ASAB and DEBK) when the nighttime enhancement and reduction in the TEC gradient were observed. Hua and Chunbo (2009) discussed the relation between ROTI index, ionospheric TEC gradient and vertical TEC. Cesaroni et al. (2015) also described the importance of the information provided by the TEC gradient variability and the role of the meridional TEC gradients in driving scintillation. By comparing the zonal and the meridional components of average and standard deviation of ΔTEC, Cesaroni et al. (2015) reported that the north–south gradients of TEC are significantly larger than their east–west counterparts, regardless of the season. For a GNSS ground-based augmentation system, Saito and Yoshihara (2017) observed an extreme spatial gradient in ionospheric total electrons (about 3.38 TECU km−1) associated with plasma bubbles. It is suggested that when scintillation events are investigated the ionospheric TEC gradient is also one of the considerable parameters.
Figure 10 presents the percentage occurrence of ionospheric irregularities over ASAB (blue) and DEBK (red) in the year 2014. The estimation of the percentage occurrence of ionospheric irregularities was made for quiet days of each month of the year 2014. The percentage occurrence of irregularities was calculated by counting the number of days in a month with ROTIave≥0.4 TECU min−1 and dividing by the number of days in a month for which the data are available, and then this value was multiplied by 100 % (Oladipo et al., 2014). Since the two stations are close to each other, the occurrence of ionospheric irregularities observed over both stations does not show major differences. Two peaks of irregularity occurrence were observed around the middle of the equinoxes (i.e., in March and September) at both stations. This could be related to the alignment of the magnetic field lines with a geographic meridian (Burke et al., 2004; Tsunoda, 2005, 2010). The seasonal variation of ionospheric irregularities exhibits an equinoctial asymmetry in its occurrence especially at the two peaks (i.e., in March and September), where the March equinox was greater than the September equinox. The maximum ROTIave observed over this station in the year 2014 was about 1.8 TECU min−1 in March 2014 and the minimum level of ROTIave was observed on December solstice.
Based on a few station observations, earlier studies indicated the equinoctial asymmetry in the occurrence of L-band scintillations which was attributed to differences in the meridional winds during two equinoxes (e.g., Nishioka et al., 2008; Maruyama et al., 2006; Otsuka et al., 2006). Nishioka et al. (2008) analyzed the occurrence characteristics of plasma bubbles using GPS-TEC obtained all over the globe and found equinoctial asymmetry in their occurrence. They suggested that equinoctial asymmetry could be due to the asymmetric distribution of integrated conductivities during analyzed periods. Using three ionosonde observations, Maruyama et al. (2006) reported that meridional wind is the key factor for the equinoctial asymmetry. Using multi-instrument observations, Sripathi et al. (2011) examined the equinoctial asymmetry in scintillation occurrence in the Indian sector and they suggested the asymmetry in the electron density distribution and meridional winds as a possible causative mechanism. Manju et al. (2012) also reported equinoctial asymmetry in ESF occurrence and they discussed the possible role of asymmetric meridional winds. Manju and Haridas (2015) observed a significant asymmetry in the threshold height between the vernal equinox and autumn equinox and underlines the distinct differences in the role of neural dynamics in ESF triggering during the two equinoxes. Based on scintillation index (S4) and GPS-TEC-derived indices, the seasonal and equinoctial asymmetry in the occurrence of ionospheric irregularities over the equatorial–low-latitude region of African was presented (Susnik and Forte, 2011; Paznukhov et al., 2012; Oladipo and Schuler, 2013b; Oladipo et al., 2014; Seba and Tsegaye, 2015; Mungufeni et al., 2016). By employing the horizontal wind model (HWM14), Seba et al. (2018) recently reported that the difference in the wind pattern between March and September is one of the factors for the equinoctial asymmetry. The local time and seasonal trends of occurrence of ionospheric irregularities observed in this study are similar to those reported in the previous studies (Aarons, 1993; Basu et al., 1988; Olwendo et al., 2013; Amabayo et al., 2014; Seba and Tsegaye, 2015). The equinoctial asymmetries in the occurrence of ionospheric irregularities observed in our case might also be due to the direction of the meridional winds during equinoxes over the stations.
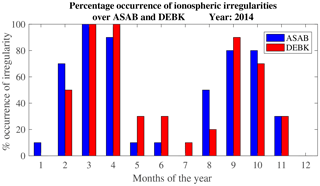
Figure 10Percentage of occurrence of ionospheric irregularities over ASAB (blue) and DEBK (red) stations during the quiet days of each month in the year 2014 based on the ROTIave index.
In terms of diurnal, monthly and seasonal behavior the enhancement and reduction in the spatial gradient of TEC and the occurrence of ionospheric irregularities appear to show similar trends. And, it is evident from the above result that the spatial gradient of TEC between two closely located stations, where the two receivers lie nearly along the same latitudes, convey insight into the relation between large-scale ionospheric irregularity occurrence and spatial gradient in TEC.
In this study, we presented for the first time the relationship between the spatial gradient of TEC between two closely located stations (ASAB and DEBK) and the occurrence of ionospheric irregularities over Ethiopia, an equatorial region, using ground-based GPS-TEC observations. The following observations are a summary of our analysis. The daytime equatorial electrojet (EEJ) derived from the H component of geomagnetic field and the real-time electric field (EEF) model (Manoj and Maus, 2012) correlates linearly and positively with correlation coefficient of C=0.6 in the year 2014. Most of the peak enhancement and reduction values of ΔTEC∕Δlong and σ(ΔTEC∕Δlong) were observed about 1–2 h later from postsunset enhancement of the EEF, which indicates that EEF and the spatial gradient of TEC have a strong relationship. In terms of month and season, the nighttime pattern of the spatial gradient of TEC (ΔTEC∕Δlong) and its standard deviation σ(ΔTEC∕Δlong) show a similar trend with ROTIave. The relation between the standard deviation of the spatial gradient of TEC, σ(ΔTEC∕Δlong), and ionospheric irregularity occurrences indicated by ROTIave were also presented. The correlation coefficient between σ(ΔTEC∕Δlong) and ROTIave was about 0.7975 (in ASAB station) and 0.7915 (in DEBK station). Both σ(ΔTEC∕Δlong) and ROTIave show maximum enhancement (reduction) during equinoctial (solstice) months. Equinoctial asymmetry was also observed in both σ(ΔTEC∕Δlong) and ROTIave, where the March equinox was greater than the September equinox. The intensity level of σ(ΔTEC∕Δlong) was stronger (weaker) when the occurrence of ionospheric irregularity is present (absent). When the occurrence of ionospheric irregularities was suppressed (for example, during geomagnetic disturbed conditions), the nighttime peak value of σ(ΔTEC∕Δlong) was smaller. Based on the above results, the strength of the spatial gradient of TEC between the two closely located stations lying along the same geomagnetic latitudes could indicate the presence of large-scale ionospheric irregularities. During the postsunset period in equinoctial months (March and April 2014), the relation between the spatial gradient of TEC/electron density and the zonal electric field was observed. The threshold value of the gradient of TEC and its standard deviation σ(ΔTEC∕Δlong) and the minimum longitudinal separation between two stations that could lead us to predict the occurrence of ionospheric irregularities are not addressed in the current study, and this will be considered in the future investigation.
The data used in this study were obtained from ftp://cddis.gsfc.nasa.gov (last access: 8 December 2018), http://geomag.org/models/PPEFM/RealtimeEF.html (CIRES, 2018), http://magnetometers.bc.edu/index.php/ (SAMBA-AMBER, 2018), https://www.intermagnet.org/ (INTERMAGNET, 2018), http://swdcwww.kugi.kyoto-u.ac.jp/ (Data Analysis Center for Geomagnetism and Space Magnetism, 2019) and http://isgi.unistra.fr/data_download.php (International Service of Geomagnetic Indices, 2019).
TD performed the analysis and drafted the manuscript with the support of JBH, and MN provided constructive scientific advice.
The authors declare that they have no conflict of interest.
Opinions, findings, and conclusions or recommendations expressed in this paper are of the author(s), and the South African National Research Foundation (NRF) accepts no liability whatsoever in this regard.
This article is part of the special issue “Vertical coupling in the atmosphere–ionosphere system”. It is a result of the 7th Vertical Coupling workshop, Potsdam, Germany, 2–6 July 2018.
We thank the Ethiopian Space Science and Technology Institute (ESSTI) for facilitating conditions to do this research. We also acknowledge the administration and staff of the Space Science Directorate of the South African National Space Agency (SANSA) for the support during the research visit of the first author to the institution. The authors would like to express their gratitude to the International GNSS Service (IGS) for providing the GPS data (ftp://cddis.gsfc.nasa.gov, last access: 8 December 2018). We thank the Cooperative Institute for Research in Environmental Sciences (CIRES) team for real-time PPEEFM model at http://geomag.org/models/PPEFM/RealtimeEF.html (last access: 27 May 2018), the World Center for Geomagnetism (WDC) Kyoto (http://wdc.kugi.kyoto-u.ac.jp/, last access: 12 March 2019) and the International Service of Geomagnetic Indices (ISGI). We are also grateful to the online AMBER (http://magnetometers.bc.edu/index.php/, last access: 12 March 2018) and INTERMAGNET (http://www.intermagnet.org/, last access: 12 March 2018) for freely providing magnetometer data. Teshome Dugassa thanks Bule Hora University for permitting study leave.
John Bosco Habarulema's work was partially supported by funding grant 112090 from the South African National Research Foundation (NRF), and Melessew Nigussie's work was supported by Air Force Office of Scientific Research, Air Force Material Command USAF, under award no. FA9550-16-1-0070.
This paper was edited by Erdal Yiğit and reviewed by two anonymous referees.
Aarons, J.: The role of the ring current in the generation or inhibition of equatorial F layer irregularities during magnetic storms, Radio Sci., 26, 1131–1149, 1991. a, b, c, d, e
Aarons, J.: The longitudinal morphology of equatorial F layer irregularities relevant to their occurrence, Space Sci. Rev., 63, 209–243, 1993. a
Aarons, J. and DasGupta, A.: Equatorial scintillations during the major magnetic storm of April 1981, Radio Sci., 19, 731–739, 1984. a, b
Aarons, J., Mendillo, M., and Yantosca, R. G.: GPS phase fluctuations in the equatorial region during sunspot minimum, Radio Sci., 32, 1535–1550, 1997. a
Abdu, M. A., Batista, I. S., Reinisch, B. W., de Souza, J. R., Sobral, J. H. A., Pedersen, T. R., Medeiros, A. F., Schuch, N. J., de Paula, E. R., and Groves, K. M.: Conjugate Point Equatorial Experiment (COPEX) campaign in Brazil: Electrodynamics highlights on spread development conditions and day to day variablity, J. Geophys. Res., 114, A04308, https://doi.org/10.1029/2008JA013749, 2009. a
Ajith, K., Tulasi Ram, S., Yamamoto, M., Otsuka, Y., and Niranjan, K.: On the fresh development of equatorial plasma bubbles around the midnight hours of June solstice, J. Geophys. Res.-Space, 121, 9051–9062, 2016. a
Alken, P., Chulliat, A., and Maus, S.: Longitudinal and seasonal structure of the ionospheric equatorial electric field, J. Geophys. Res.-Space, 118, 1298–1305, 2013. a, b
Amabayo, E., Jurua, E., Cilliers, P., and Habarulema, J.: Climatology of ionospheric scintillations and TEC trend over the Ugandan region, Adv. Space Res., 53, 734–743, 2014. a
Anderson, D., Anghel, A., Yumoto, K., Ishitsuka, M., and Kudeki, E.: Estimating daytime vertical E×B drift velocities in the equatorial F-regionx using ground-based magnetometer observations, Geophys. Res. Lett., 29, 1596, https://doi.org/10.1029/2001GL014562, 2002. a, b, c
Anderson, D., Anghel, A., Chau, J., and Veliz, O.: Daytime vertical E×B drift velocities inferred from ground-based magnetometer observations at low latitudes, Space Weather, Space Weather, 2, S11001, https://doi.org/10.1029/2004SW000095, 2004. a, b
Anderson, D., Anghel, A., Chau, J. L., and Yumoto, K.: Global, low-latitude, vertical E×B drift velocities inferred from daytime magnetometer observations, Space Weather, 4, S08003, https://doi.org/10.1029/2005SW000193, 2006. a, b
Arikan, F., Nayir, H., Sezen, U., and Arikan, O.: Estimation of single station interfrequency receiver bias using GPS-TEC, Radio Sci., 43, RS4004, https://doi.org/10.1029/2007RS003785, 2008. a
Basu, S. and Basu, S.: Equatorial scintillations-A review, J. Atmos. Terr. Phys., 43, 473–489, 1981. a
Basu, S., MacKenzie, E., and Basu, S.: Ionospheric constraints on VHF/UHF communications links during solar maximum and minimum periods, Radio Sci., 23, 363–378, 1988. a
Basu, S., Kudeki, E., Basu, S., Valladares, C., Weber, E., Zengingonul, H., Bhattacharyya, S., Sheehan, R., Meriwether, J., Biondi, M., Kuenzler, H., and Espinoza, J.: Scintillations, plasma drifts, and neutral winds in the equatorial ionosphere after sunset, J. Geophys. Res., 101, 26795–26809, 1996. a
Batista, I., Abdu, M., and Bittencourt, J.: Equatorial F region vertical plasma drifts: Seasonal and longitudinal asymmetries in the American sector, J. Geophys. Res.-Space, 91, 12055–12064, 1986. a
Bhattacharyya, A., Beach, T., Basu, S., and Kintner, P.: Nighttime equatorial ionosphere: GPS scintillations and differential carrier phase fluctuations, Radio Sci., 35, 209–224, 2000. a
Biktash, L. Z.: Role of the magnetospheric and ionospheric currents in the generation of the equatorial scintillations during geomagnetic storms, Ann. Geophys., 22, 3195–3202, https://doi.org/10.5194/angeo-22-3195-2004, 2004. a, b, c
Bolaji, O., Adebiyi, S., and Fashae, J.: Characterization of ionospheric irregularities at different longitudes during quiet and disturbed geomagnetic conditions, J. Atmos. Sol.-Terr. Phy., 182, 93–100, 2019. a, b
Burke, W. J., Gentile, L. C., Huang, C. Y., Valladares, C. E., and Su, S. Y.: Longitudinal variability of equatorial plasma bubbles observed by DMSP and ROCSAT-1, J. Geophys. Res., 19, A12301, https://doi.org/10.1029/2004JA010583, 2004. a, b, c
Cesaroni, C., Spogli, L., Alfonsi, L., De Franceschi, G., Ciraolo, L., Monico, J. F. G., Scotto, C., Romano, V., Aquino, M., and Bougard, B.: L-band scintillations and calibrated total electron content gradients over Brazil during the last solar maximum, J. Space Weather Spac., 5, A36, https://doi.org/10.1051/swsc/2015038, 2015. a, b, c, d, e, f, g, h
Chu, F. D., Liu, J. Y., Takahashi, H., Sobral, J. H. A., Taylor, M. J., and Medeiros, A. F.: The climatology of ionospheric plasma bubbles and irregularities over Brazil, Ann. Geophys., 23, 379–384, https://doi.org/10.5194/angeo-23-379-2005, 2005. a
CIRES: Geomagnetism, available at: http://geomag.org/models/PPEFM/RealtimeEF.html, last access: 27 May 2018. a
Crain, D., Heelis, R., and Bailey, G.: Effects of electrical coupling on equatorial ionospheric plasma motions: When is the F region a dominant driver in the low-latitude dynamo?, J. Geophys. Res.-Space, 98, 6033–6037, 1993. a
Dabas, R., Singh, L., Lakshmi, D., Subramanyam, P., Chopra, P., and Garg, S.: Evolution and dynamics of equatorial plasma bubbles: Relationships to E×B drift, postsunset total electron content enhancements, and equatorial electrojet strength, Radio Sci., 38, 1075, https://doi.org/10.1029/2001RS002586, 2003. a, b
Data Analysis Center for Geomagnetism and Space Magnetism: World Data Center for Geomagnetism, Kyoto, available at: http://swdcwww.kugi.kyoto-u.ac.jp/, last access: 12 March 2019. a
Dubazane, M. B. and Habarulema, J. B.: An empirical model of vertical plasma drift over the African sector, Space Weather, 16, 619–635, 2018. a
Dugassa, T., Habarulema, J. B., and Nigussie, M.: Longitudinal variability of occurrence of ionospheric irregularities over the American, African and Indian regions during geomagnetic storms, Adv. Space Res., 63, 2609–2622, https://doi.org/10.1016/j.asr.2019.01.001, 2019. a, b, c
Echer, E., Tsurutani, B., and Gonzalez, W.: Interplanetary origins of moderate (−100 nT < Dst ≤ −50 nT) geomagnetic storms during solar cycle 23 (1996–2008), J. Geophys. Res.-Space, 118, 385–392, 2013. a
Farley, D., Balsey, B., Woodman, R., and McClure, J.: Equatorial spread F: Implications of VHF radar observations, J. Geophys. Res., 75, 7199–7216, 1970. a
Farley, D. T., Bonelli, E., Fejer, B. G., and Larsen, M. F.: The prereversal enhancement of the zonal electric field in the equatorial ionosphere, J. Geophys. Res., 91, 13723–13728, 1986. a
Fejer, B.: Low latitude electrodynamics plasma drifts: a review, J. Atmos. Terr. Phys., 53, 677–693, 1991. a
Fejer, B., Jensen, J., and Su, S.: Quiet time equatorial F region vertical plasma drift model derived from ROCSAT-1 observations, J. Geophys. Res., 113, A05304, https://doi.org/10.1029/2007JA012801, 2008. a
Fejer, B. G. and Scherliess, L.: Mid-and low-latitude prompt-penetration ionospheric zonal plasma drifts, Geophys. Res. Lett., 25, 3071–3074, 1998. a
Fejer, B. G., Scherliess, L., and de Paula, E. R.: Effects of the vertical plasma drift velocity on the generation and evolution of equatorial spread F, J. Geophys. Res., 104, 19859–19869, https://doi.org/10.1029/1999JA900271, 1999. a, b, c
Foster, J.: Quantitative investigation of ionospheric density gradients at mid latitudes, in: Proceedings of the Institute of Navigation ION 2000 Conference, The Institute of Navigation, Anaheim, CA, 2000. a
Ghamry, E., Lethy, A., Arafa-Hamed, T., and Abd Elaal, E.: A comprehensive analysis of the geomagnetic storms occurred during 18 February and 2 March 2014, NRIAG Journal of Astronomy and Geophysics, 5, 263–268, 2016. a
Hajra, R., Chakraborty, S., Mazumdar, S., and Alex, S.: Evolution of equatorial irregularities under varying electrodynamical conditions: a multitechnique case study from Indian longitude zone, J. Geophys. Res.-Space, 117, A08331, https://doi.org/10.1029/2012JA017808, 2012. a
Heelis, R., Kendall, P., Moffett, R., Windle, D., and Rishbeth, H.: Electrical coupling of the E-and F-regions and its effect on F-region drifts and winds, Planet. Space Sci., 22, 743–756, 1974. a
Hua, H. W. C. Y. S. and Chunbo, Z.: Study of Ionospheric TEC Horizontal Gradient by Means of GPS Observations, Chinese Journal of Space Science, 2, 183–187, 2009. a
Huang, C.-S.: Effects of the postsunset vertical plasma drift on the generation of equatorial spread F, Prog. Earth Planet. Sc., 5, 3, https://doi.org/10.1186/s40645-017-0155-4, 2018. a
Hysell, D. and Burcham, J.: Ionospheric electric field estimates from radar observations of the equatorial electrojet, J. Geophys. Res.-Space, 105, 2443–2460, 2000. a
INTERMAGNET: International Real-time Magnetic Observatory Network, available at: https://www.intermagnet.org/, last access: 12 March 2018. a
International Service of Geomagnetic Indices: Geomagnetic Indices, available at: http://isgi.unistra.fr/data_download.php, last access: 12 March 2019. a
Jakowski, N., Leitinger, R., and Ciraolo, L.: Behaviour of large scale structures of the electron content as a key parameterfor range errors in GNSS applications, Ann. Geophys., 47, 2–3, 2004. a
Jakowski, N., Stankov, S. M., and Klaehn, D.: Operational space weather service for GNSS precise positioning, Ann. Geophys., 23, 3071–3079, https://doi.org/10.5194/angeo-23-3071-2005, 2005. a
Kassa, T. and Damtie, B.: Ionospheric irregularities over Bahir Dar, Ethiopia during selected geomagnetic storms, Adv. Space Res., 60, 121–129, 2017. a, b, c
Kelley, M., Fejer, B. G., and Gonzales, C.: An explanation for anomalous equatorial ionospheric electric fields associated with a northward turning of the interplanetary magnetic field, Geophys. Res. Lett., 6, 301–304, 1979. a
Kelley, M. C.: The Earth's ionosphere: plasma physics and electrodynamics, Vol. 96, Academic Press, San Diego, 2009. a, b
Lee, J., Pullen, S., Datta-Barua, S., and Enge, P.: Assessment of ionosphere spatial decorrelation for global positioning system-based aircraft landing systems, J. Aircraft, 44, 1662–1669, 2007. a, b
Lee, J., Datta-Barua, S., Zhang, G., Pullen, S., and Enge, P.: Observations of low-elevation ionospheric anomalies for ground-based augmentation of GNSS, Radio Sci., 46, RS6005, https://doi.org/10.1029/2011RS004776, 2011. a
Lee, J. H., Pullen, S., Datta-Barua, S., and Enge, P.: Assessment of nominal ionosphere spatial decorrelation for laas, in: 2006 IEEE/ION Position, Location, And Navigation Symposium, Stanford University, Stanford, California 94305-4085, 2010. a
Loewe, C. A. and Prölss, G. W.: Classification and mean behavior of magnetic storms, J. Geophys. Res.-Space, 102, 14209–14213, 1997. a
Luo, M., Pullen, S., Akos, D., Xie, G., Datta-Barua, S., Walter, T., and Enge, P.: Assessment of ionospheric impact on LAAS using WAAS supertruth data, in: Proceedings of The ION 58th Annual Meeting, 24–26, Citeseer, Inst. of Nav., Albuquerque, N.M, 175–186, 2002. a
Ma, G. and Maruyama, T.: A super bubble detected by dense GPS network at East Asian longitudes, Geophys. Res. Lett., 33, L21103, https://doi.org/10.1029/2006GL027512, 2006. a
Magdaleno, S., Herraiz, M., Altadill, D., and Benito, A.: Climatology characterization of equatorial plasma bubbles using GPS data, J. Space Weather Spac., 7, A3, https://doi.org/10.1051/swsc/2016039, 2017. a
Manju, G. and Haridas, M. M.: On the equinoctial asymmetry in the threshold height for the occurrence of equatorial spread F, J. Atmos. Sol.-Terr. Phy., 124, 59–62, 2015. a
Manju, G., Devasia, C., and Ravindran, S.: The seasonal and solar cycle variations of electron density gradient scale length, vertical drift and layer height during magnetically quiet days: Implications for Spread F over Trivandrum, India, Earth Planets Space, 61, 1339–1343, 2009. a
Manju, G., Haridas, M., Ravindran, S., Pant, T. K., and Ram, S. T.: Equinoctial asymmetry in the occurrence of equatorial spread-F over Indian longitudes during moderate to low solar activity period 2004–2007, Indian Journal of Radio and Space Physics, 41, 240–246, 2012. a, b
Manoj, C. and Maus, S.: A real-time forecast service for the ionospheric equatorial zonal electric field, Space Weather, 10, S09002, https://doi.org/10.1029/2012SW000825, 2012. a, b, c
Martinis, C. R., Mendillo, M. J., and Aarons, J.: Toward a synthesis of equatorial spread F onset and suppression during geomagnetic storms, J. Geophys. Res., 110, A07306, https://doi.org/10.1029/2003JA010362, 2005. a, b
Maruyama, T., Saito, S., Kawamura, M., Nozaki, K., Krall, J., and Huba, J. D.: Equinoctial asymmetry of a low-latitude ionosphere-thermosphere system and equatorial irregularities: evidence for meridional wind control, Ann. Geophys., 27, 2027–2034, https://doi.org/10.5194/angeo-27-2027-2009, 2009. a, b
Mendillo, M., Baumgardner, J., Pi, X., Sultan, P. J., and Tsunoda, R.: Onset conditions for equatorial spread F, J. Geophys. Res.-Space, 97, 13865–13876, 1992. a
Mendillo, M., Lin, B., and Aarons, J.: The application of GPS observations to equatorial aeronomy, Radio Sci., 35, 885–904, 2000. a, b
Mendillo, M., Meriwether, J., and Biondi, M.: Testing the thermospheric neutral wind suppression mechanism for day-to-day variability of equatorial spread F, J. Geophys. Res., 106, 3655–3663, 2001. a, b, c, d
Muella, M., De Paula, E., Kantor, I., Batista, I., Sobral, J., Abdu, M., Kintner, P., Groves, K., and Smorigo, P.: GPS L-band scintillations and ionospheric irregularity zonal drifts inferred at equatorial and low-latitude regions, J. Atmos. Sol.-Terr. Phy., 70, 1261–1272, 2008. a
Mungufeni, P., Jurua, E., and Habarulema, J.: Trends of ionospheric irregularities over African low latitude region during quiet geomagnetic conditions., J. Atmos. Sol.-Terr. Phy., 138–139, 261–267, https://doi.org/10.1016/j.jastp.2016.01.015, 2016. a, b
Mushini, S. C., Jayachandran, P. T., Langley, R. B., MacDougall, J. W., and Pokhotelov, D.: Improved amplitude and phase scintillation indices derived from wavelet detrended high latitude GPS data, GPS Solut., 16, 363–373, https://doi.org/10.1007/s10291-011-0238-4, 2011. a
Nava, B., Radicella, S., Leitinger, R., and Coïsson, P.: Use of total electron content data to analyze ionosphere electron density gradients, Adv. Space Res., 39, 1292–1297, 2007. a
Nayak, C., Tsai, L.-C., Su, S.-Y., Galkin, I., Caton, R., and Groves, K.: Suppression of ionospheric scintillation during St. Patrick's Day geomagnetic super storm as observed over the anomaly crest region station Pingtung, Taiwan: A case study, Adv. Space Res., 60, 396–405, https://doi.org/10.1016/j.asr.2016.11.036, 2017. a
Nishioka, M., Saito, A., and Tsugawa, T.: Occurrence characteristics of plasma bubble derived from global ground-based GPS receiver networks, J. Geophys. Res., 113, A05301, https://doi.org/10.1029/2007JA012605, 2008. a, b, c, d
Oladipo, O. A. and Schuler, T.: Magnetic storm effect on the occurrence of ionospheric irregularities at an equatorial station in the African sector, Ann. Geophys., 56, A0565, https://doi.org/10.4401/ag-6247, 2013a. a, b
Oladipo, O. A. and Schuler, T.: Equatorial ionospheric irregularities using GPS TEC derived index, Atmos. Sol. Terr. Phys., 92, 78–82, 2013b. a, b, c, d, e, f
Oladipo, O. A., Adeniyi, J. O., Olawepo, A. O., and Doherty, P. H.: Large-scale ionospheric irregularities occurrence at Ilorin, Nigeria, Space Weather, 12, 300–305, https://doi.org/10.1002/2013SW000991, 2014. a, b, c, d, e
Olwendo, J., Cilliers, P., Weimin, Z., Ming, O., and Yu, X.: Validation of ROTI index for ionospheric amplitude scintillation measurements in a low latitude region over Africa, Radio Sci., 53, 876–887, https://doi.org/10.1029/2017RS006391, 2018. a
Olwendo, O., Baluku, T., Baki, P., Cilliers, P., Mito, C., and Doherty, P.: Low latitude ionospheric scintillation and zonal irregularity drifts observed with GPS-SCINDA system and closely spaced VHF receivers in Kenya, Adv. Space Res., 51, 1715–1726, https://doi.org/10.1016/j.asr.2012.12.017, 2013. a
Ossakow, S. L.: Spread-F theories – A review, J. Atmos. Terr. Phys., 43, 437–452, 1981. a
Otsuka, Y., Shiokawa, K., and Ogawa, T.: Equatorial ionospheric scintillations and zonal irregularity drifts observed with closely spaced GPS receivers in Indonesia, J. Meteorol. Soc. Jpn., 84, 343–351, 2006. a
Otsuka, Y. and Ogawa, T.: VHF radar observations of nighttime F-region field-aligned irregularities over Kototabang, Indonesia, Earth Planets Space, 61, 431–437, 2009. a
Paznukhov, V. V., Carrano, C. S., Doherty, P. H., Groves, K. M., Caton, R. G., Valladares, C. E., Seemala, G. K., Bridgwood, C. T., Adeniyi, J., Amaeshi, L. L. N., Damtie, B., D'Ujanga Mutonyi, F., Ndeda, J. O. H., Baki, P., Obrou, O. K., Okere, B., and Tsidu, G. M.: Equatorial plasma bubbles and L-band scintillations in Africa during solar minimum, Ann. Geophys., 30, 675–682, https://doi.org/10.5194/angeo-30-675-2012, 2012. a, b
Pi, X., Mannucci, A. J., Lindqdwister, U. J., and Ho, C.: Monitoring of Global Ionospheric Irregularities using the worldwide GPS, Geophys. Res. Lett., 24, 2283–2286, https://doi.org/10.1029/97GL02273, 1997. a, b, c, d
Pradipta, R. and Doherty, P. H.: Assessing the occurrence pattern of large ionospheric TEC gradients over the Brazilian airspace, J. Inst. Navig., 63, 335–343, 2016. a
Radicella, S. M., Nava, B., Coïsson, P., Kersley, L., and Bailey, G. J.: Effects of gradients of the electron density on Earth-space communications, Ann. Geophys., 47, 1227–1246, 2004. a, b
Rama Rao, P. V. S., Gopi Krishna, S., Niranjan, K., and Prasad, D. S. V. V. D.: Study of spatial and temporal characteristics of L-band scintillations over the Indian low-latitude region and their possible effects on GPS navigation, Ann. Geophys., 24, 1567–1580, https://doi.org/10.5194/angeo-24-1567-2006, 2006a. a, b
Rama Rao, P. V. S., Gopi Krishna, S., Niranjan, K., and Prasad, D. S. V. V. D.: Temporal and spatial variations in TEC using simultaneous measurements from the Indian GPS network of receivers during the low solar activity period of 2004–2005, Ann. Geophys., 24, 3279–3292, https://doi.org/10.5194/angeo-24-3279-2006, 2006b. a
Rastogi, R. and Woodman, R.: Spread F in equatorial ionograms associated with reversal of horizontal F region electric field, Ann. Geophys., 34, 31–36, 1978. a
Rastogi, R. G., Kitamura, T., and Kitamura, K.: Geomagnetic field variations at the equatorial electrojet station in Sri Lanka, Peredinia, Ann. Geophys., 22, 2729–2739, https://doi.org/10.5194/angeo-22-2729-2004, 2004. a
Rastogi, R. G. and Klobuchar, J. A.: Ionospheric electron content within the equatorial F2 layer anomaly belt, J. Geophys. Res., 95, 19045–19052, 1990. a
Ratnam, D. V., Vishnu, T. R., and Harsha, P. B. S.: Ionospheric Gradients Estimation and Analysis of S-Band Navigation Signals for NAVIC System, IEEE Access, 6, 66954–66962, 2018. a
Ravi Chandra, K., Satya Srinivas, V., and Sarma, A.: Investigation of ionospheric gradients for GAGAN application, Earth Planets Space, 61, 633–635, 2009. a, b
Ray, S., Paul, A., and Dasgupta, A.: Equatorial scintillations in relation to the development of ionization anomaly, Ann. Geophys., 24, 1429–1442, 2006. a
Rishbeth, H.: Polarization fields produced by winds in the equatorial F-region, Planet. Space Sci., 19, 357–369, 1971. a
Rungraengwajiake, S., Supnithi, P., Saito, S., Siansawasdi, N., and Saekow, A.: Ionospheric delay gradient monitoring for GBAS by GPS stations near Suvarnabhumi airport, Thailand, Radio Sci., 50, 1076–1085, 2015. a, b, c, d
Saito, S. and Yoshihara, T.: Evaluation of extreme ionospheric total electron content gradient associated with plasma bubbles for GNSS Ground-Based Augmentation System, Radio Sci., 52, 951–962, 2017. a, b, c
SAMBA-AMBER: SAMBA-AMBER Magnetometers Data Center, available at: http://magnetometers.bc.edu/index.php/, last access: 12 March 2018. a
Sardón, E. and Zarraoa, N.: Estimation of total electron content using GPS data: How stable are the differential satellite and receiver instrumental biases?, Radio Sci., 32, 1899–1910, 1997. a
Seba, E. and Nigussie, M.: Investigating the effect of geomagnetic storm and equatorial electrojet on equatorial ionospheric irregularity over East African sector, Adv. Space Res., 58, 1708–1719, 2016. a
Seba, E. and Tsegaye, K. G.: Characterization of ionospheric scintillation at a geomagnetic equatorial region station, Adv. Space Res., 56, 2057–2063, 2015. a, b, c, d
Seba, E. B., Nigussie, M., and Moldwin, M. B.: The relationship between equatorial ionization anomaly and nighttime equatorial spread F in East Africa, Adv. Space Res., 62, 1737–1752, 2018. a, b, c
Seemala, G. and Valladares, C.: Statistics of total electron content depletions observed over the South American continent for the year 2008, Radio Sci., 46, RS5019, https://doi.org/10.1029/2011RS004722, 2011. a
Sreeja, V., Devasia, C. V., Sudha Ravindran, and Tarun Kumar Pant: Observational evidence for the plausible linkage of Equatorial Electrojet (EEJ) electric field variations with the post sunset F-region electrodynamics, Ann. Geophys., 27, 4229–4238, https://doi.org/10.5194/angeo-27-4229-2009, 2009. a
Sripathi, S., Kakad, B., and Bhattacharyya, A.: Study of equinoctial asymmetry in the Equatorial Spread F (ESF) irregularities over Indian region using multi-instrument observations in the descending phase of solar cycle 23, J. Geophys. Res., 116, A11302, https://doi.org/10.1029/2011JA016625., 2011. a
Su, S.-Y., Liu, C., Ho, H., and Chao, C.: Distribution characteristics of topside ionospheric density irregularities: Equatorial versus midlatitude regions, J. Geophys. Res.-Space, 111, A06305, https://doi.org/10.1029/2005JA011330, 2006. a
Sultan, P.: Linear theory and modeling of the Rayleigh-Taylor instability leading to the occurrence of equatorial spread F, J. Geophys. Res.-Space, 101, 26875–26891, 1996. a
Susnik, A. and Forte, B.: Ionospheric scitillation activity measured in the African sector, General Assembly and Scientific Symposium, XXXth URSI, Istanbul, Turkey, 2011. a
Takahashi, H., Wrasse, C. M., Denardini, C. M., Pádua, M. B., de Paula, E. R., Costa, S. M. A., Otsuka, Y., Shiokawa, K., Monico, J. G., Ivo, A., and Sant'Anna, N.: Ionospheric TEC weather map over South America, Space Weather, 14, 937–949, 2016. a
Tsunoda, R. T.: On the enigma of day-to-day variability in Wave structure in equatorial Spread F, Geophys. Res. Lett., 32, L08103, https://doi.org/10.1029/2005GL022512, 2005. a
Tsunoda, R. T.: On seeding equatorial spread F during solstices, Geophys. Res. Lett., 37, L05102, https://doi.org/10.1029/2010GL042576, 2010. a
Tulasi Ram, S., Rama Rao, P. V. S., Niranjan, K., Prasad, D. S. V. V. D., Sridharan, R., Devasia, C. V., and Ravindran, S.: The role of post-sunset vertical drifts at the equator in predicting the onset of VHF scintillations during high and low sunspot activity years, Ann. Geophys., 24, 1609–1616, https://doi.org/10.5194/angeo-24-1609-2006, 2006. a, b
Tulasi Ram, S., Rama Rao, P. V. S., Prasad, D. S. V. V. D., Niranjan, K., Raja Babu, A., Sridharan, R., Devasia, C. V., and Sudha Ravindran: The combined effects of electrojet strength and the geomagnetic activity (Kp-index) on the post sunset height rise of the F-layer and its role in the generation of ESF during high and low solar activity periods, Ann. Geophys., 25, 2007–2017, https://doi.org/10.5194/angeo-25-2007-2007, 2007. a, b
Uemoto, J., Maruyama, T., Saito, S., Ishii, M., and Yoshimura, R.: Relationships between pre-sunset electrojet strength, pre-reversal enhancement and equatorial spread-F onset, Ann. Geophys., 28, 449–454, https://doi.org/10.5194/angeo-28-449-2010, 2010. a, b
Valladares, C., Basu, S., Groves, K., Hagan, M., Hysell, D., Mazzella Jr., A., and Sheehan, R.: Measurement of the latitudinal distribution of total electron content during equatorial spread-F events, J. Geophys. Res., 106, 29133–29152, 2001. a, b, c
Valladares, C. E., Villalobos, J., Sheehan, R., and Hagan, M. P.: Latitudinal extension of low-latitude scintillations measured with a network of GPS receivers, Ann. Geophys., 22, 3155–3175, https://doi.org/10.5194/angeo-22-3155-2004, 2004. a, b
Watthanasangmechai, K., Yamamoto, M., Saito, A., Tsunoda, R., Yokoyama, T., Supnithi, P., Ishii, M., and Yatini, C.: Predawn plasma bubble cluster observed in Southeast Asia, J. Geophys. Res.-Space, 121, 5868–5879, 2016. a
Wernik, A. and Liu, C.: Ionospheric irregularities causing scintillation of GHz frequency radio signals, J. Atmos. Terr. Phys., 36, 871–879, 1974. a
Wiens, R. H., Ledvina, B. M., Kintner, P. M., Afewerki, M., and Mulugheta, Z.: Equatorial plasma bubbles in the ionosphere over Eritrea: occurrence and drift speed, Ann. Geophys., 24, 1443–1453, https://doi.org/10.5194/angeo-24-1443-2006, 2006. a
Woodman, R.: Vertical drift velocities and East–West electric fields at the magnetic equator, J. Geophys. Res., 75, 6249–6259, https://doi.org/10.1029/JA075i031p06249, 1970. a
Yizengaw, E., Moldwin, M. B., Mebrahtu, A., Damtie, B., Zesta, E., Valladares, C. E., and Doherty, P.: Comparison of storm time equatorial ionospheric electrodynamics in the African and American sectors, J. Atmos. Sol.-Terr. Phy., 73, 156–163, https://doi.org/10.1016/j.jastp.2010.08.008, 2011. a
Yizengaw, E., Zesta, E., A. M. M. B., Damtie, B., Mebrahtu, A., Valladares, C. E., and Pfaff, R. F.: Longitudinal differences of ionospheric vertical density distribution and equatorial electrodynamics, J. Geophys. Res., 117, A07312, https://doi.org/10.1029/2011JA017454, 2012. a
Yizengaw, E., Moldwin, M. B., Zesta, E., Biouele, C. M., Damtie, B., Mebrahtu, A., Rabiu, B., Valladares, C. F., and Stoneback, R.: The longitudinal variability of equatorial electrojet and vertical drift velocity in the African and American sectors, Ann. Geophys., 32, 231–238, https://doi.org/10.5194/angeo-32-231-2014, 2014. a
Yoshihara, T., Sakai, T., Fujii, N., and Saitoh, A.: An investigation of local-scale spatial gradient of ionospheric delay using the nation-wide GPS network data in Japan, in: ION National Technical Meeting, San Diego, CA, 2005. a