the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Numerical simulation of oblique ionospheric heating by powerful radio waves
Moran Liu
Xiang Wang
Bin Bin Ni
Zhengyu Zhao
In this paper, we investigate the ionospheric heating by oblique incidence of powerful high-frequency (HF) radio waves using three-dimensional numerical simulations. The ionospheric electron density and temperature perturbations are examined by incorporating the ionospheric electron transport equations and ray-tracing algorithm. The energy distribution of oblique incidence heating waves in the ionosphere is calculated by the three-dimensional ray-tracing algorithm. The calculation takes into consideration the electric field of heating waves in the caustic region by the plane wave spectral integral method. The simulation results show that the ionospheric electron density and temperature can be disturbed by oblique incidence of powerful radio waves, especially in the caustic region of heating waves. The oblique ionospheric heating with wave incidence parallel and perpendicular to the geomagnetic field in the mid-latitude ionosphere is explored by simulations, results of which indicate that the ionospheric modulation is more effective when the heating wave propagates along the magnetic field line. Ionospheric density and temperature striations in the caustic region due to thermal self-focusing instability are demonstrated, as well as the time evolution of the corresponding fluctuation spectra.
Keywords. Ionosphere (active experiments)
Since the Luxembourg effect was discovered in the 1930s, the ionospheric modification by using powerful HF radio waves has been an important tool for investigating the physical processes of interactions between ionospheric plasma and electromagnetic waves. A large number of phenomena during ionospheric heating experiments have been reported, including a few exciting discoveries such as artificial ionization layer, enhanced plasma line, stimulated electromagnetic emissions (SEEs), enhanced airglow, and artificial field-aligned irregularities (FAIs) to name just a few (Pedersen et al., 2010; Hagfors et al., 1983; Thidé et al., 1983; Bernhardt et al., 1991; Inhester et al., 1981; Weinstock, 1975; Thome and Blood, 1974). The scientific concerns of ionospheric heating include a large range of plasma physics topics involving Ohmic/Joule heating, parametric instability, particle acceleration, Langmuir turbulence, VLF/ELF/ULF wave generation, etc. (Foster et al., 1983; Wong et al., 1971; Ungstrup et al., 1979; DuBois et al., 1990; Brinca et al., 1981).
Thermal effect due to Ohmic absorption is one of the principal physical processes in ionospheric heating, which has been intensively investigated by many researchers (Shoucri et al., 1984; Hansen et al., 1992a, b; Gustavsson et al., 2010; Mantas et al., 1981). Large-scale ionospheric electron density/temperature changes due to thermal redistribution and ionospheric plasma transport can be generated by the Ohmic heating mechanism. Energy of powerful heating waves is imparted to the electrons through acceleration of the electrons in the wave electric field, which could induce the following thermal process. The dissociative recombination coefficient decreases as the electron temperature increases. As a result, the electron density in the D/E region of low altitude increases. However, in the F region, where the diffusion coefficient is much larger than the low-altitude ionosphere, a thermal pressure gradient develops and drives the electrons expanding along the magnetic field line. Consequently, the pressure gradient causes electron density depletion in the reflection region of heating waves for overdense heating (Hansen et al., 1989, 1992b; Blaunstein, 1996; Mingaleva et al., 2003, 2008). Although Ohmic heating is not expected to produce evident changes in ionospheric electron density and temperature, the large-scale spatial disturbance of electron density structure in the F region can alter the propagation path of the heating waves and induce focusing/defocusing effects, which have been reported in many experiments (Hansen et al., 1990, 1992a). Considerable efforts have been focused on the simulation study of the Ohmic absorption in the vertical incidence heating (Meltz et al., 1974; Mantas et al., 1981; Shoucri et al., 1984; Gurevich, 1978).
Another thermal effect revealed during vertical incidence heating is the thermal self-focusing instability. Both observational evidence and simulation studies indicate that the FAIs of kilometer scale, which are manifested in the development of artificial spread F and ducted propagation modes, are generated by the thermal self-focusing instability (Georges, 1970; Perkins and Valeo, 1974; Duncan and Behnke, 1978; Guzdar et al., 1998; Kuo and Djuth, 1988; Gurevich et al., 2002a; Gondarenko et al., 2005, 2006). The thermal self-focusing instability has also been of interest in many plasma environments, such as controlled nuclear fusion and laboratory laser plasma research (Johnson et al., 1974). Gurevich (1978) indicate that there is no absolute threshold for self-focusing instability excitation. However, it was demonstrated in a number of studies that the scale size of the FAIs/striations excited by self-focusing instability is related to the heating wave power (Duncan and Behnke, 1978; Guzdar et al., 1996). Perkins and Goldman (1981) have also proposed a theoretical calculation for undersense heating, which can excite the so-called thermal filamentation instability. The scale spectrum of the FAIs generated by thermal self-focusing instability ranges from a broadband due to the nonlinear saturation (Gurevich, 1978).
Modern ionospheric heaters can transmit the radio waves with different elevation angles (Rietveld et al., 1993; Oyama et al., 2006), which means not just an overhead ionosphere region, but also that the remote ionosphere can be modulated by powerful radio wave incidence. Warren et al. (1982) proposed a method to extend ray-tracing calculation into a strong focusing region and applied it to simulate the ionospheric electron temperature and density changes due to oblique heating (Field and Warber, 1985; Field et al., 1990). Hinkel-Lipsker et al. (1993) introduced an ionospheric oblique heating model by coupling the ray-tracing numerical method and ionospheric plasma transport equations. This model is applied to a daytime ionospheric oblique heating and predicts a density increase in the lower ionosphere. Experimental investigations of the influences of powerful oblique radio waves on the ionosphere indicate that the large-scale ionospheric disturbances generated by heating can produce additional traces on the diagnostic ionogram (Bochkarev, 1997; Bochkarev et al., 1997).
The oblique heating cannot produce the parametric instability as the vertical incident heating due to the fact that the frequency matching condition is not satisfied by the frequency of oblique heating wave and local plasma. Only if the angle of the heating wave is within the Spitze cone does the heating wave reach the critical layer and induce the Langmuir parametric instability (Mjølhus et al., 2003; Eliasson, 2008; Eliasson et al., 2015a, b; Eliasson and Papadopoulos, 2016). Another hotspot region is the upper hybrid (UH) resonant height, where thermal parametric and resonant instability can be induced and small-scale FAIs can be observed (Kelley et al., 1995; Franz et al., 1999). However, for oblique heating with large incidence angles, the reflection height could be much lower than the height of critical frequency and UH frequency. For this sense, there are relatively few studies devoted to the subject of ionospheric oblique heating by powerful radio waves, in comparison to vertical heating studies. However, the investigation of the ionospheric oblique heating still has merits on topics such as (a) magnetic zenith effects (Kosch et al., 2000; Gurevich et al., 2002b; Pedersen et al., 2003), (b) ELF/VLF wave generation via the spatially modulated ionospheric heating (Milikh et al., 2007; Kuo et al., 2008), and (c) the ionospheric heating effects on the HF skywave over-the-horizon radar (Hinkel-Lipsker et al., 1993; Sales et al., 1993).
In the studies presented by Zhou et al. (2016), the evolution of the large-scale ionospheric electron density and temperature modulation by powerful electromagnetic waves is investigated by a three-dimensional vertical heating model. The simulation results demonstrated that the ionospheric electron density/temperature changes are generated by the vertical heating and the embedded large-scale FAIs are induced by thermal self-focusing instability, which shows that the thermal process with diversity scales plays an important role in the ionospheric heating.
In the present study, we expand our model established by Zhou et al. (2016) to the three-dimensional ionospheric heating by oblique incidence of powerful HF radio waves. The energy distribution of heating waves in the caustic region is calculated with the plane wave spectral integral method so that the ionospheric electron density and temperature disturbances in the caustic region are investigated. We also concentrate on the analysis of heating wave incidence parallel and perpendicular to the magnetic field line in the mid-latitude ionosphere. The outline of this paper is as follows. In Sect. 2, the model of the ionospheric oblique heating is introduced, as well as the calculation of energy distribution of heating waves in the caustic region. In Sect. 3, we present the disturbance of the ionospheric electron density and temperature with heating waves transmitted along the geomagnetic field lines and perpendicular to the geomagnetic field. We also investigate the large-scale electron density and temperature FAIs generated by thermal self-focusing instability for oblique heating. The related physical processes for the presented simulation results are discussed in Sect. 4. The summary of this study is presented in Sect. 5.
2.1 Ray tracing and electric field calculation
In the study of the oblique heating ionosphere, the electric field in the caustic area is difficult to calculate by geometric optics approximation, where the electric field is enhanced by the overlap of heating waves. Budden (1976) presented the calculation of an electric field in the caustic region of the isotropic medium, and obtained the numerical result by ray tracing. Field et al. (1990) used the numerical method of Warren et al. (1982) to resolve the equation and obtained the electric field at any given point, including the caustic area and reflection region.
The electric field along the ray path was calculated in the process of ray tracing, including the electric field in the caustics. Because of invalidity of the geometrical optics near-reflection region and the self-focusing action of the caustics, it is difficult to calculate the electric field. Budden (1976) gives the angular spectral integral approximation for an electromagnetic field in the vicinity of the caustic, which was used in this paper. In this method, the phase integral of heating waves is needed.
Budden (1976) showed that a field component E in the ionosphere can be approximated as the plane wave spectral integral
where S1, S2, and C are complex direction cosines in free space and the refractive index n is calculated by using the O-mode wave dispersion relation according to the Appleton–Hamilton formula (Budden, 1988):
Let θ be the angle between the wave vector in free space and vertical direction, and C=cos θ, ; G is specified by the transmitter; x, y, and z are Cartesian coordinates of the field point; is the free space wave number, where λ is wavelength. Then the function q is defined as , and then . Ai is Airy's integral, and z0 is reflection height.
In the process of computation, the case of two dimensions was considered. So let y=0, and then the x–z plane was the magnetic meridian plane. For most applications, G is fairly simple . Then the approximate solution of Eq. (1) becomes
where . The electric field of any point in the ray path could be calculated by Eq. (3). Near a caustic surface, any point has two rays intersecting. Subscripts “a” and “b” are defined as two different rays, which interact at one point in the caustic region. Thus Pa and Pb are the two phase paths, from Eq. (1) with y=0. Sa, Sb are the two values of S1. Then and . Let , . Budden (1988) gave the approximate solution,
2.2 Model of ionospheric heating
A model of ionospheric heating is established on Ohmic heating theory, which is used to explain many phenomena in the HF heating ionosphere experiment. Ohmic heating theory is based on three equations, the momentum equation, continuity equation and electron energy equation, which are as follows.
Momentum equation:
Continuity equation:
Electron energy equation:
All terms in the three equations are explained in Zhou et al. (2016). In the electron energy equation, term Q0 represents the steady-state source term in the absence of the heating and term Le represents the electron cooling rate. The term QHF is obtained by calculating the work of the electric field to the electron (Gurevich, 1978):
where e is electron charge, E0 is electric field, m is electron mass, υe is collision frequency between electron and other particles, and ω is frequency of heating wave.
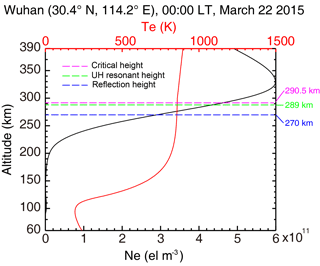
Figure 1The ionospheric electron density (black line) and temperature profiles (red line) used for the ionospheric background obtained from the IRI-2012 model. The purple dotted line indicates the critical height of the heating frequency. The green line indicates the upper-hybrid resonant height. The blue line indicates the reflection height of the heating waves in the ionosphere.
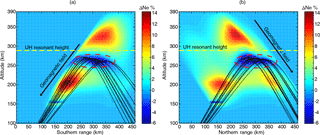
Figure 2An example of the ray path of HF heating waves. The heating waves are transmitted along the geomagnetic field lines (a) and perpendicular to the geomagnetic field (b). The background is the ionospheric electron density change at a heating duration time of 180 s in response to the oblique heating waves. The heating ERP is 300 MW and the heating frequency is 6 MHz.
3.1 Ionospheric background and simulation parameter
In this section, the results of the simulation are presented. Wuhan (30.4∘ N, 114.0∘ E), which is typical mid-latitude, is selected as the location of the heating transmitter. The magnetic dip of Wuhan is 45∘, which is nearly identical to that of Arecibo (Carlson et al., 2016). Figure 1 shows the initial ionospheric electron density and temperature profile at 00:00 LT adopted from the international reference ionosphere model (IRI-2012) (Bilitza et al., 2011). Density and temperature of the neutral particles are obtained by the NRLMSISE-00 model (Picone et al., 2002). We choose the 00:00 LT of equinox of 2015, so that the absorption in the D region can be neglected. The effective radiated power (ERP) of the heater is set as 300 MW (∼ 83 dBW). The frequency of the heating wave is 6 MHz. The beam width is 5∘. According to the “secant law” of ionospheric oblique propagation (Davis, 1989), the approximation reflection height of the oblique heating wave is around 270 km.
The ray-tracing region of heating waves is 0–390 km in height, 0–500 km in the north–south direction and −66 to 66 km in the west–east direction. The heater is set at the origin (0, 0, 0). The step of the ray tracing is 1 km in the ray propagation direction. The plasma transport region is 90–390 km in height, −20 to 530 km in the north–south direction and −76 to 76 km in the west–east direction. The grid size of the plasma transport procedure is 1 km in altitude, north–south direction and west–east direction. In the simulation region, we treat the ionosphere as horizontally stratified. The time step of the simulation is 1 ms.
3.2 Ray tracing and three-dimensional results
It is well established that the direction between the magnetic field line and the heating wave propagation is important for the results of oblique heating (Rietveld et al., 2003; Gondarenko et al., 2006). Accordingly, we investigate two specific situations of the oblique heating, which is the heating wave transmitted along the local magnetic field line and perpendicular to the local magnetic field line.
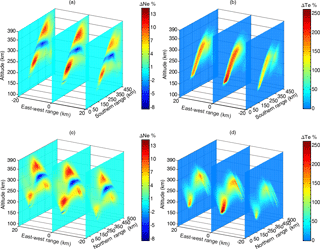
Figure 3The ionospheric electron density and temperature change due to oblique ionospheric heating. (a) The electron density change in three slices with the heating wave incidence parallel to the magnetic field line. (b) The electron temperature change in three slices with the heating wave incidence parallel to the magnetic field line. (c) The electron density change in three slices with the heating wave incidence perpendicular to the magnetic field line. (d) The ionospheric electron temperature change presented in three slices with the heating wave incidence perpendicular to the magnetic field line.
Figure 2 shows the ray path of the heating wave propagation in the heated ionosphere. Figure 2a shows the heating wave transmitted along the geomagnetic field lines in the magnetic meridian plane. Figure 2b shows the heating wave transmitted perpendicularly to the geomagnetic field in the magnetic meridian plane. The background is the ionospheric electron density change at a heating duration time of 180 s in response to the powerful heating waves. The red dashed circles identify the so-called exterior caustic region of the heating waves. Figure 2a shows the depletion of electron density in the caustic region and the enhancement in the upper/lower area along the field line. Figure 2b also shows ionospheric electron density enhancement at ∼ 200 km before the heating wave has reached the reflection height.
Figure 3 shows the three-dimensional results after 180 s heating. Three magnetic meridian planes are selected to show the results, which intersect the ground 20 km west of the heating facility, at the heater, and 20 km east of the heating facility. Figure 3a and b show the electron and temperature disturbances in percentage in the three planes with the heating wave incidence parallel to the magnetic field line. Figure 3c and d show the electron and temperature disturbances in percentage in three slices with the heating wave incidence perpendicular to the magnetic field line. Figure 3 shows the strongest heating effects in the center plane. Figure 3b shows that enhancements of the electron temperature are the largest at low altitudes (∼ 150 km) and become weak with heating wave propagation, which is due to the geometric spreading and absorption effects. While the situation of a heating wave transmitted perpendicular to the field line is different, as shown in Fig. 3d, significant changes in electron temperature can also be found in the caustic region.
3.3 Time evolution of ionospheric electron density and temperature disturbances
Figures 4 and 5 show the time evolution of the ionospheric electron density and temperature changes in the center magnetic meridian plane with heating wave incidence parallel to the local magnetic field line at heating times of 0.5, 5, 30, and 180 s. As shown in Figs. 4 and 5, at the earlier time of heating (t = 0.5 s), one can observe changes in ionospheric electron temperature in two regions, namely the low-altitude ionosphere and caustic region. The electron density disturbance at earlier times mainly develops in the caustic region. At the next time (t = 5, 30 s), due to the thermal conduction and plasma diffusion, the disturbance expands to a broad region especially along the field lines. The electron temperature does not change significantly after t = 30 s. One can also observe the striations of the electron density and temperature grow up from the caustic region.
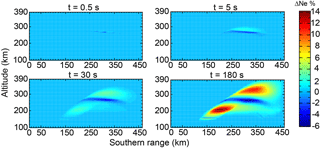
Figure 4The evolution of the ionospheric electron density changes in the center meridian plane with heating wave incidence parallel to the magnetic field line at different heating duration times.
Figures 6 and 7 are the same format as Figs. 4 and 5, but with heating wave incidence perpendicular to the local magnetic field line. At a heating time of t = 0.5 s, the electron density and temperature mostly develop in the low-altitude and caustic region. Subsequently, at the time later than t = 30 s, the electron density and temperature have undergone a significant development, which is quite different from the initial state. The redistribution of electron density and temperature due to transport processes can be observed as well as the formation of the striated structure near the caustic region. At a heating time of 180 s, the large-scale FAIs are most prominent along the heating wave path after the reflection region, where the heating wave propagates parallel to the field lines.
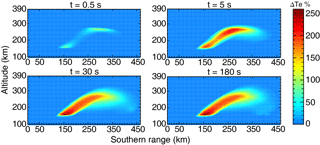
Figure 5The evolution of the ionospheric electron temperature changes in the center meridian plane with heating wave incidence parallel to the magnetic field line at different heating duration times.
At the beginning of heating, electron density changes more slowly than electron temperature. From Figs. 4 to 7, it can be found that the typical saturation time of the large-scale electron density changes is on the order of tens of seconds in the F region, while the large-scale electron temperature becomes stable after seconds to tens of seconds.
By comparing the ionospheric electron and temperature perturbations with heating wave incidence parallel and perpendicular to the field line, noticeable differences in the disturbed ionospheric electron density and temperature can be observed.
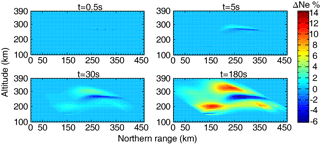
Figure 6The evolution of the ionospheric electron density changes in the center meridian plane with heating wave incidence perpendicular to the magnetic field line at different heating duration times.
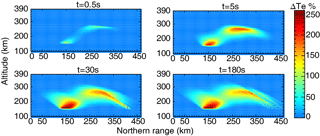
Figure 7The evolution of the ionospheric electron temperature changes in the center meridian plane with heating wave incidence perpendicular to the magnetic field line at different heating duration times.
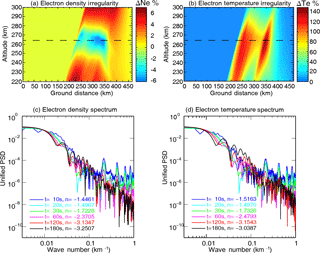
Figure 8The electron density and temperature irregularity with heating wave incidence parallel to the magnetic field line. (a) The electron density irregularity in the center meridian plane at a heating time of 180 s. (b) The electron temperature irregularity in the center meridian plane at a heating time of 180 s. (c) The spatial power spectral density (PSD) of electron density irregularity at different heating times. (d) The spatial power spectral density of electron temperature irregularity at different heating times.
3.4 Large-scale field aligned irregularities and their spatial spectrum
Figure 8a and b present the large-scale electron density and temperature irregularities after a heating time of 180 s with a heating wave transmitted parallel to the local magnetic field. Figure 8c and d show the electron density and temperature disturbance spectrum at the height (∼ 264 km) in the caustic region with heating wave transmitted parallel to the local magnetic field. Different colors of lines indicate different heating times. The spectra present a typical power-law () feature. The spectral index n is calculated at different heating times. Figure 9 is the same format as Fig. 8, but with heating wave transmitted perpendicular to the local magnetic field. As can be seen from Figs. 8 and 9, at the heating time of t = 180 s, the magnitudes of the averaged density and temperature fluctuations in the caustic region are about 6 and 140 %. At the first stage, namely t = 10 and 20 s, the spectrum of the FAIs is not the typical power-law type. As the evolution of the electron density and temperature perturbations, the power-law spectra come to be more evident and steeper. The saturated spectra of electron density and temperature are slightly different for heating wave incidence parallel and perpendicular to the magnetic field line. The spectra indices of the saturated FAIs are found to be in a range of −3.0 ± 0.4 (parallel incidence) to −3.4 ± 0.4 (perpendicular incidence). The density and temperature striations are formed because of the focusing of the pump wave. The characteristic scale of these structures is a few kilometers in the cross-field direction and several tens of kilometers in the aligned-field direction, whilst the outer scale of the structures is determined by the energy distribution of the pump wave.
In the above analysis, we report the simulation results of the ionospheric oblique heating by powerful electromagnetic waves. The simulation results show the increase in the ionospheric electron temperature due to Ohmic absorption along the ray path of the heating waves. In the caustic region, strong Ohmic heating of ionospheric electrons occurs owing to the strongly focused electric field. Enhanced thermal pressure and plasma diffusion lead to the electron density depletion in the caustic region and the enhancement both above and below the caustic region along the geomagnetic field line. In our simulations, we have found large ionospheric electron perturbations (∼ 6 % ΔNe∕Ne and ∼ 120 % ΔTe∕Te), which in magnitude are comparable to the vertical heating results of Zhou et al. (2016) but smaller than that (density depletions of > 25 % and > 200 % ΔTe∕Te) of Hansen et al. (1992a). The simulation results thereby indicate that although energy losses due to geometric spreading of oblique propagation are larger than for vertical incidence, the ionospheric electron density and temperature can be disturbed considerably due to the electric field enhancement of the focused heating wave in the caustic region. Identical conclusions were obtained in previous studies (Field et al., 1990; Hinkel-Lipsker et al., 1993).
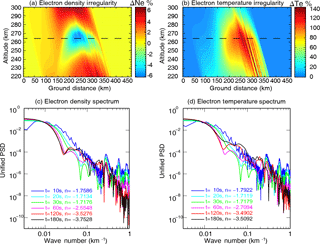
Figure 9The same format as Fig. 8, but with heating wave incidence perpendicular to the magnetic field line.
By comparing the results of the heating wave incidence along and perpendicular to the local magnetic field line, we find large changes in ionospheric electron density and temperature with heating waves propagating parallel to the field line. From Figs. 4 and 5, it is seen that ionospheric electron density and temperature changes are large before the reflection, which mainly owes to the diffusive effects along the magnetic field line. However, for heating waves transmitted perpendicularly to the magnetic field line, as shown in Figs. 6 and 7, significant disturbances of ionospheric electron density and temperature can be observed after the reflection, where the heating wave propagates parallel to the magnetic field line. Therefore, these simulation results imply that the heating wave propagation along the magnetic field can produce larger ionospheric electron density and temperature disturbances.
In high-latitude ionospheric heating experiments, the heater beams transmitted in the magnetic zenith have been reported in a number of studies. Gurevich et al. (2002b) have suggested an explanation of the magnetic zenith effect based on heating wave self-focusing on striations, which can cause strong amplification of the electron temperature in the heated region. Gurevich et al. (2005) also applied this theory to interpret the Ohmic heating of the ionospheric plasma near the heating wave reflection point for mid-latitude ionospheric heating. The magnetic-zenith effect is considered to be a consequence of the strong nonlinear process of plasma structuring and anomalous electron heating determined by the development of striations, i.e., magnetic-field-aligned inhomogeneities. The other explanation based on a large-scale cavity stretched along the magnetic field line was presented in Leyser and Nordblad (2009) and Nordblad and Leyser (2010). They claimed that the O-mode heating wave could be guided into an L wave along the magnetic field line with the formation of the large-scale cavity, which facilitates strong excitation of UH phenomena and related anomalous heating. Honary et al. (2011) reported the strongest electron temperature enhancement with heating waves directed along the magnetic field line and suggest that electrostatic waves trapped in striations are localized above the level where the plasma frequency coincides with the frequency of the pump wave. Our simulation results present the “magnetic zenith effect” in ionospheric oblique heating from the aspect of the thermal effect.
Field-aligned irregularities produced by oblique heating have been reported in many experiments (Nasyrov and Strekalov, 1995; Nasyrov et al., 1998; Uryadov et al., 2007). It is shown that for different incidence angles of a high-power wave on the ionosphere, maximum scattered-signal amplitude is observed in the case where the heating wave is parallel to the magnetic field. Gondarenko et al. (2004, 2005) report the large-scale FAI evolution based on the full-wave propagation model. Their simulation results demonstrate that the FAIs generated and developed due to the local heating show strong enhancement of electron temperature inside the depletions elongated along the magnetic field line. They also present the aspect angle dependence of the formation of the large-scale FAIs. The electron temperature of FAIs increases up to more than 200 % of the background when the incident beam is near the magnetic zenith (Gondarenko et al., 2006), which is consistent with the observation in the heating experiment at the EISCAT high-latitude facility (Rietveld et al., 2003; Honary et al., 2011). However, since they mainly focused on the high-latitude heating experiment, the thermal self-focusing instability excited in the caustic region during ionospheric oblique heating has not brought sufficient attention. The simulation results in Figs. 8 and 9 demonstrate that the focused electric field in the caustic region is strong enough to excite the thermal self-focusing instability, which presents as the large-scale FAIs of electron density and temperature. Both the spectra of electron density and temperature perturbations present the power-law feature. The temporal evolution of the spectra indicates that the timescale of the development of the large-scale FAIs is about tens of seconds as determined by the nonlinear saturation. Note that the spectrum is of power-law type only at the late times during the FAI evolution process. Simulation results of Gondarenko et al. (2005) indicate that both the saturation timescale of electron density and temperature of FAIs are about hundreds of milliseconds. Figure 9 also indicates that the saturation timescale depends on the scale of the irregularities. Keskinen and Basu (2003) present the results of the growth rate of thermal self-focusing instability and show that the timescale is about an order of seconds. However, our simulation results (Figs. 8 and 9) show that the saturation timescale could be tens of seconds or minutes, which is quite consistent with the observational results in Kosch et al. (2007). Gondarenko et al. (2006) compare the power spectral density of electron density at high latitude in three different directions of the heater beam, vertical, 6 and 12∘ (field-aligned) between the wave propagation direction and the vertical, and show that the power spectral indices are −4, −3 and −1.6, respectively. Farley et al. (1983) analyze the satellite data from the eastern portions of the path through the heater beam in an ionospheric heating experiment at Arecibo and find that the power spectral index is −3.3. Our simulation presents the spatial power spectral indices at different times. The power spectral indices decrease with time. The spectra indices of the saturated FAIs (−3.0 ± 0.4 in parallel incidence and −3.4 ± 0.4 in perpendicular incidence) are consistent with Farley et al. (1983).
In the present study, ionospheric heating with oblique incidence of powerful radio waves is studied. Based on a three-dimensional simulation that includes the plasma transport equation and ray-tracing algorithm, we have quantitatively explored the ionospheric electron density and temperature changes. Our main conclusions are summarized as follows.
Our simulation results demonstrate that the large-scale (on the order of kilometers and seconds) ionospheric electron density and temperature disturbances are generated by the oblique heating. Due to Ohmic absorption, ionospheric electron temperature increases in the region of ray paths of the heating waves. The simulation results also present the ionospheric electron density depletion in the caustic region and electron density enhancement in the upper/lower region along the field line as a consequence of the thermal pressure and plasma diffusion process. Due to the focused electric field of the heating waves in the caustic region, the changes in the electron density and temperature are more significant. In our simulations, the approximate 6 % depletion of electron density and 120 % enhancement of electron temperature are presented in the caustic region for the nighttime ionosphere.
We have investigated the magnetic field angle effects on the ionospheric oblique heating. Three-dimensional simulations of the ionospheric electron density and temperature changes with heating waves transmitted parallel and perpendicular to the local magnetic field lines are explored and compared. The simulation results indicate that the electron density and temperature have changed more significantly with heating wave propagation parallel to the magnetic field lines, which is consistent with the reports in high-latitude heating experiments (Rietveld et al., 2003; Tereshchenko et al., 2004). The simulation results also suggest promising application in low- and mid-latitude heating experiments.
The simulation results show that large-scale FAIs due to the thermal self-focusing instability can be generated by the oblique heating at nighttime. Simulations of the heating wave incidence both parallel and perpendicular to the magnetic field lines indicate that the focused energy of heating waves gives rise to the enhanced thermal energy of heating waves in the caustic region, and can consequently excite the thermal self-focusing instability. The large-scale FAIs of electron density and temperature generated by the thermal self-focusing instability can spread along the magnetic field lines with tens of kilometers. The characteristic transverse scale of the FAIs is about several kilometers. The spatial spectrum of the electron density and temperature perturbations at the approximate center of the caustic region is of a typical power-law type. The spectra indices of the saturated FAIs due to nonlinear evolution are found to be in a range of −3.0 ± 0.4 (parallel incidence) and −3.4 ± 0.4 (perpendicular incidence), which is in accordance with the previous simulations and the observations of both vertical and oblique heating (Tereshchenko et al., 2004; Gondarenko et al., 2006).
The data have been uploaded to https://pan.baidu.com/s/1obGgzemX6dk8vQzHRK6_hg (Liu, 2018).
The authors declare that they have no conflict of interest.
This work was supported by the National Natural Science Foundation of China
(NSFC grant nos. 41574146, 41704155 and 41774162).
The topical editor, Ana G. Elias, thanks Thomas Leyser
and one anonymous referee for help in evaluating this paper.
Bernhardt, P. A., Scales, W. A., Grach, S. M., Keroshtin, A. N., Kotik, D. S., and Polyakov, S. V.: Excitation of artificial airglow by high power radio waves from the “Sura” ionospheric heating facility, Geophys. Res. Lett., 18, 1477–1480, 1991.
Bilitza, D., McKinnell, L. A., Reinisch, B., and Fuller-Rowell, T.: The International Reference Ionosphere (IRI) today and in the future, J. Geodesy, 85, 909–920, https://doi.org/10.1007/s00190-010-0427-x, 2011.
Blaunstein, N.: Changes of the electron concentration profile during local heating of the ionospheric plasma, J. Atmos. Terr. Phys., 58, 1345–1354, 1996.
Bochkarev, G. S.: Influence of the ionosphere, modified by powerful oblique radiowaves, on HF radio wave propagation, J. Atmos. Sol.-Terr. Phy., 59, 2295–2304, 1997.
Bochkarev, G. S., Krasheninnikov, I. V., and Sales, G. S.: The effects of powerful oblique radio transmission on the ionosphere on vertical sounding data, J. Atmos. Sol.-Terr. Phy., 59, 2305–2311, https://doi.org/10.1016/S1364-6826(96)00124-1, 1997.
Brinca, A. L.: Enhancing whistler wave-electron interaction by the use of specially modulated VLF wave injection, J. Geophys. Res.-Space, 86, 792–800, 1981.
Budden, K. G.: Radio caustics and cusps in the ionosphere, P. Roy. Soc. Lond. A Mat., 350, 143–164, 1976.
Budden, K. G.: The Propagation of Radio Waves: the Theory of Radio Waves of Low Power in the Ionosphere and Magnetosphere, Cambridge University Press, Cambridge, 1988.
Carlson, H. C., Djuth, F. T., and Zhang, L. D.: Creating space plasma from the ground, J. Geophys. Res.-Space, 122, 978–999, https://doi.org/10.1002/2016JA023380, 2016.
Davies, K.: Ionospheric radio, Peter Peregrinus Ltd., London, 1989.
DuBois, D. F., Rose, H. A., and Russell, D.: Excitation of strong Langmuir turbulence in plasmas near critical density: application to HF heating of the ionosphere, J. Geophys. Res.-Space, 95, 21221–21272, 1990.
Duncan, L. M. and Behnke, R. A.: Observations of self-focusing electromagnetic waves in the ionosphere, Phys. Rev. Lett., 41, 998–1001, 1978.
Eliasson, B.: Full-scale simulation study of the generation of topside ionospheric turbulence using a generalized Zakharov model, Geophys. Res. Lett., 35, L11104, https://doi.org/10.1029/2008GL033866, 2008.
Eliasson, B. and Papadopoulos, K.: HF wave propagation and induced ionospheric turbulence in the magnetic equatorial region, J. Geophys. Res.-Space, 121, 2727–2742, https://doi.org/10.1002/2015JA022323, 2016.
Eliasson, B., Milikh, G., Shao, X., Mishin, E. V., and Papadopoulos, K.: Incidence angle dependence of Langmuir turbulence and artificial ionospheric layers driven by high-power HF-heating, J. Plasma Phys., 81, 415810201, https://doi.org/10.1017/S0022377814000968, 2015.
Farley, D. T., LaHoz, C., and Fejer, B. G.: Studies of the self-focusing instability at Arecibo, J. Geophys. Res., 88, 2093–2102, https://doi.org/10.1029/JA088iA03p02093, 1983.
Field, E. C. and Warber, C. R.: Ionospheric heating with obliquely incident waves, Geophys. Res. Lett., 12, 761–763, https://doi.org/10.1029/GL012i011p00761, 1985.
Field Jr., E. C., Bloom, R. M., and Kossey, P. A.: Ionospheric heating with oblique high-frequency waves, J. Geophys. Res., 95, 21179–21186, https://doi.org/10.1029/JA095iA12p21179, 1990.
Foster, J. C., StMaurice, J. P., and Abreu, V. J.: Joule heating at high latitudes, J. Geophys. Res.-Space, 88, 4885–4897, 1983.
Franz, T. L., Kelley, M. C., and Gurevich, A. V.: Radar backscattering from artificial field-aligned irregularities, Radio Sci., 34, 465–475, 1999.
Georges, T. M.: Amplification of ionospheric heating and triggering of “spread-F” by natural irregularities, J. Geophys. Res., 75, 6436–6438, 1970.
Gondarenko, N. A., Guzdar, P. N., Ossakow, S. L., and Bernhardt, P. A.: Perfectly matched layers for radio wave propagation in inhomogeneous magnetized plasmas, J. Comput. Phys., 194, 481–504, 2004.
Gondarenko, N. A., Ossakow, S. L., and Milikh, G. M.: Generation and evolution of density irregularities due to self-focusing in ionospheric modifications, J. Geophys. Res., 110, A09304, https://doi.org/10.1029/2005JA011142, 2005.
Gondarenko, N. A., Ossakow, S. L., and Milikh, G. M.: Nonlinear evolution of thermal self-focusing instability in ionospheric modifications at high latitudes: aspect angle dependence, Geophys. Res. Lett., 33, L16104, https://doi.org/10.1029/2006GL025916, 2006.
Gurevich, A.: Nonlinear Phenomena in the Ionosphere, Springer Science and Business Media, New York, 1978.
Gurevich, A., Fremouw, E., Secan, J., and Zybin, K.: Large scale structuring of plasma density perturbations in ionospheric modifications, Phys. Lett. A, 301, 307–314, https://doi.org/10.1016/S0375-9601(02)00901-5, 2002a.
Gurevich, A. V., Zybin, K. P., Carlson, H. C., and Pedersen, T.: Magnetic zenith effect in ionospheric modifications, Phys. Lett. A, 305, 264–274, 2002b.
Gurevich, A., Zybin, K., and Carlson, H.: Magnetic-zenith effect, Radiophys. Quantum El., 48, 686–699, https://doi.org/10.1007/s11141-005-0113-7, 2005.
Gustavsson, B., Rietveld, M. T., Ivchenko, N. V., and Kosch, M. J.: Rise and fall of electron temperatures: ohmic heating of ionospheric electrons from underdense HF radio wave pumping, J. Geophys. Res., 115, A12332, https://doi.org/10.1029/2010JA015873, 2010.
Guzdar, P. N., Chaturvedi, P. K., Papadopoulos, K., Keskinen, M. J., and Ossakow, S. L.: The self-focusing instability in the presence of density irregularities in the ionosphere, J. Geophys. Res., 101, 2453–2460, https://doi.org/10.1029/95JA02975, 1996.
Guzdar, P. N., Chaturvedi, P. K., Papadopoulos, K., and Ossakow, S. L.: The thermal self-focusing instability near the critical surface in the high-latitude ionosphere, J. Geophys. Res., 103, 2231–2238, 1998.
Guzdar, P. N., Chaturvedi, P. K., Papadopoulos, K., and Ossakow, S. L.: Observations of enhanced plasma lines by EISCAT during heating experiments, Radio Sci., 18, 861–866, 1983.
Hansen, J. D., Morales, G. J., and Maggs, J. E.: Daytime saturation of thermal cavitons, J. Geophys. Res.-Space, 94, 6833–6840, 1989.
Hansen, J. D., Morales, G. J., Duncan, L. M., Maggs, J. E., and Dimonte, G.: Large-scale ionospheric modifications produced by nonlinear refraction of an HF wave, Phys. Rev. Lett., 65, 3285–3288, https://doi.org/10.1103/PhysRevLett.65.3285, 1990.
Hansen, J. D., Morales, G. J., Duncan, L. M., and Dimonte, G.: Large-scale HF-induced ionospheric modifications: experiments, J. Geophys. Res., 97, 113–122, 1992a.
Hansen, J. D., Morales, G. J., and Maggs, J. E.: Large-scale HF-induced ionospheric modifications: theory and modeling, J. Geophys. Res., 97, 17019–17032, 1992b.
Hinkel-Lipsker, D. E., Shoucri, M. M., Smith, T. M., Wagner, T. M., Hansen, J. D., and Morales, G. J.: Modeling of high-frequency oblique propagation and heating in the ionosphere, Radio Sci., 28, 819–837, https://doi.org/10.1029/93RS01578, 1993.
Honary, F., Borisov, N., Beharrell, M., and Senior, A.: Temporal development of the magnetic zenith effect, J. Geophys. Res., 116, A06309, https://doi.org/10.1029/2010JA016029, 2011.
Inhester, B., Das, A. C., and Fejer, J. A.: Generation of small-scale field-aligned irregularities in ionospheric heating experiments, J. Geophys. Res.-Space, 86, 9101–9106, 1981.
Johnson, L. C. and Chu, T. K.: Measurements of electron density evolution and beam self-focusing in a laser-produced plasma, Phys. Rev. Lett., 32, 517–520, https://doi.org/10.1103/PhysRevLett.32.517, 1974.
Kelley, M. C., Arce, T. L., Salowey, J., Sulzer, M., Armstrong, W. T., Carter, M., and Duncan, L.: Density depletions at the 10-m scale induced by the Arecibo heater, J. Geophys. Res., 100, 17367–17376, https://doi.org/10.1029/95JA00063, 1995.
Keskinen, M. J. and Basu, S.: Thermal self-focusing instability in the high-latitude ionosphere, Radio Sci., 38, 1095, https://doi.org/10.1029/2003RS002906, 2003.
Kosch, M. J., Rietveld, M. T., Hagfors, T., and Leyser, T. B.: High latitude HF-induced airglow displaced equatorwards of the pump beam, Geophys. Res. Lett., 27, 2817–2820, 2000.
Kosch, M. J., Pedersen, T., Mishin, E., Starks, M., Gerken-Kendall, E., Sentman, D., and Watkins, B.: Temporal evolution of pump beam self-focusing at the High-Frequency Active Auroral Research Program, J. Geophys. Res., 112, A08304, https://doi.org/10.1029/2007JA012264, 2007.
Kuo, S. P. and Djuth, F. T.: A thermal instability for the spread-F echoes from HF-heated ionosphere, Geophys. Res. Lett., 15, 1345–1348, 1988.
Kuo, S. P., Wu, Y. L., Pradipta, R., Cohen, J. A., and Lee, M. C.: VLF wave generation by amplitude-modulated HF heater waves at Gakona, Alaska, Geophys. Res. Lett., 35, L13101, https://doi.org/10.1029/2008GL034414, 2008.
Leyser, T. B. and Nordblad, E.: Self-focused radio frequency L wave pumping of localized upper hybrid oscillations in high-latitude ionospheric plasma, Geophys. Res. Lett., 36, L24105, https://doi.org/10.1029/2009GL041438, 2009.
Liu, M.: Data of results in this paper, available at: https://pan.baidu.com/s/1obGgzemX6dk8vQzHRK6_hg, last access: 10 June 2018.
Mantas Jr, G. P., Carlson, H. C., and LaHoz, C. H.: Thermal response of the F region ionosphere in artificial modification experiments by HF radio waves, J. Geophys. Res., 86, 561–574, https://doi.org/10.1029/JA086iA02p00561, 1981.
Milikh, G. M. and Papadopoulos, K.: Enhanced ionospheric ELF/VLF generation efficiency by multiple timescale modulated heating, Geophys. Res. Lett., 34, L20804, https://doi.org/10.1029/2007GL031518, 2007.
Mingaleva, G. I., Mingalev, V. S., and Mingalev, I. V.: Simulation study of the high-latitude F-layer modification by powerful HF waves with different frequencies for autumn conditions, Ann. Geophys., 21, 1827–1838, https://doi.org/10.5194/angeo-21-1827-2003, 2003.
Mingaleva, G. I., Mingalev, V. S., and Mingalev, I. V.: Model prediction of the most effective frequency for the large-scale modification of the midlatitude ionospheric F2 layer by powerful HF radiowaves, Geomagn. Aeronomy, 48, 66–74, 2008.
Mjølhus, E., Helmersen, E., and DuBois, D. F.: Geometric aspects of HF driven Langmuir turbulence in the ionosphere, Nonlin. Processes Geophys., 10, 151–177, https://doi.org/10.5194/npg-10-151-2003, 2003.
Nasyrov, A. M. and Strekalov, V. A.: Dynamical stability of plasma irregularities produced by powerful radio wave in the F region of the ionosphere, Adv. Space Res., 15, 37–40, 1995.
Nasyrov, A. M., Nasyrov, I. A., and Bochkarev, G. S.: The development of small-scale irregularities in the ionosphere disturbed by powerful oblique HF radio waves, Adv. Space Res., 21, 701–704, 1998.
Nordblad, E. and Leyser, T. B.: Ray tracing analysis of L mode pumping of the ionosphere, with implications for the magnetic zenith effect, Ann. Geophys., 28, 1749–1759, https://doi.org/10.5194/angeo-28-1749-2010, 2010.
Oyama, S. I., Watkins, B. J., Djuth, F. T., Kosch, M. J., Bernhardt, P. A., and Heinselman, C. J.: Persistent enhancement of the HF pumpinduced plasma line measured with a UHF diagnostic radar at HAARP, J. Geophys. Res.-Space, 111, A06309, https://doi.org/10.1029/2005JA011363, 2006.
Pedersen, T. R., McCarrick, M., Gerken, E., Selcher, C., Sentman, D., Carlson, H. C., and Gurevich, A.: Magnetic zenith enhancement of HF radioinduced airglow production at HAARP, Geophys. Res. Lett., 30, 1169, https://doi.org/10.1029/2002GL016096, 2003.
Pedersen, T., Gustavsson, B., Mishin, E., Kendall, E., Mills, T., Carlson, H. C., and Snyder, A. L.: Creation of artificial ionospheric layers using highpower HF waves, Geophys. Res. Lett., 37, L02106, https://doi.org/10.1029/2009GL041895, 2010.
Perkins, F. W. and Valeo, E. J.: Thermal self-focusing of electromagnetic waves in plasmas, Phys. Rev. Lett., 32, 1234–1237, 1974.
Perkins, F. W. and Goldman, M. V.: Self-focusing of radio waves in an underdense ionosphere, J. Geophys. Res., 86, 600–608, https://doi.org/10.1029/JA086iA02p00600, 1981.
Picone, J. M., Hedin, A. E., Drob, D. P., and Aikin, A. C.: NRLMSISE-00 empirical model of the atmosphere: statistical comparisons and scientific issues, J. Geophys. Res.-Space, 107, 1468, https://doi.org/10.1029/2002JA009430, 2002.
Rietveld, M. T., Kohl, H., Kopka, H., and Stubbe, P.: Introduction to ionospheric heating at Tromsø – I. Experimental overview, J. Atmos. Terr. Phys., 55, 577–599, 1993.
Rietveld, M. T., Kosch, M. J., Blagoveshchenskaya, N. F., Kornienko, V. A., Leyser, T. B., and Yeoman, T. K.: Ionospheric electron heating, optical emissions, and striations induced by powerful HF radio waves at high latitudes: aspect angle dependence, J. Geophys. Res., 108, 1141, https://doi.org/10.1029/2002JA009543, 2003.
Sales, G. S.: Ionospheric Modification by High Power, Obliquely Propagated HF Radio Wave Transmissions. Part 1. Experimental (No. SCIENTIFIC-6), Massachusetts Univ. Lowell Center for Atmospheric Research, Lowell, 1993.
Shoucri, M. M., Morales, G. J., and Maggs, J. E.: Ohmic heating of the polar F region by HF pulses, J. Geophys. Res., 89, 2907–2917, 1984.
Tereshchenko, E. D., Khudukon, B. Z., Gurevich, A. V., Zybin, K. P., Frolov, V. L., Myasnikov, E. N., and Carlson, H. C.: Radio tomography and scintillation studies of ionospheric electron density modification caused by a powerful HF-wave and magnetic zenith effect at mid-latitudes, Phys. Lett. A, 325, 381–388, https://doi.org/10.1016/j.physleta.2004.03.055, 2004.
Thidé, B., Derblom, H., Hedberg, Å., Kopka, H., and Stubbe, P.: Observations of stimulated electromagnetic emissions in ionospheric heating experiments, Radio Sci., 18, 851–859, 1983.
Thome, G. D. and Blood, D. W.: First observations of RF backscatter from field-aligned irregularities produced by ionospheric heating, Radio Sci., 9, 917–921, 1974.
Ungstrup, E., Klumpar, D. M., and Heikkila, W. J.: Heating of ions to superthermal energies in the topside ionosphere by electrostatic ion cyclotron waves, J. Geophys. Res.-Space, 84, 4289–4296, 1979.
Uryadov, V. P., Vertogradov, G. G., Vertogradov, V. G., Komrakov, G. P., Cherkashin, Y. N., and Vas'kov, V. V.: Field-aligned scattering of HF radio waves under conditions of action of high-power oblique radio waves on the ionosphere, Radiophys. Quantum El., 50, 611–618, 2007.
Warren, R. E., DeWitt, R. N., and Warber, C. R.: A numerical method for extending ray trace calculations of radio fields into strong focusing regions, Radio Sci., 17, 514–520, https://doi.org/10.1029/RS017i003p00514, 1982.
Weinstock, J.: Theory of enhanced airglow during ionospheric modifications, J. Geophys. Res., 80, 4331–4345, 1975.
Wong, A. Y. and Taylor, R. J.: Parametric excitation in the ionosphere, Phys. Rev. Lett., 27, 644–647, https://doi.org/10.1103/PhysRevLett.27.644, 1971.
Zhou, C., Ni, B. B., Wang, X., Liu, M. R., Xu, X., Wang, C., and Zhao, Z. Y.: A numerical study of large-scale ionospheric modulation due to the thermal process by powerful wave heating, J. Geophys. Res.-Space, 121, 2704–2714, https://doi.org/10.1002/2016JA022355, 2016.





