the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Quantifying the relationship between the plasmapause and the inner boundary of small-scale field-aligned currents, as deduced from Swarm observations
Hermann Lühr
This paper presents a statistical study of the equatorward boundary of small-scale field-aligned currents (SSFACs) and investigates the relation between this boundary and the plasmapause (PP). The PP data used for validation were derived from in situ electron density observations of NASA's Van Allen Probes. We confirmed the findings of a previous study by the same authors obtained from the observations of the CHAMP satellite SSFAC and the NASA IMAGE satellite PP detections, namely that the two boundaries respond similarly to changes in geomagnetic activity, and they are closely located in the near midnight MLT sector, suggesting a dynamic linkage. Dayside PP correlates with the delayed time history of the SSFAC boundary. We interpreted this behaviour as a direct consequence of co-rotation: the new PP, formed on the night side, propagates to the dayside by rotating with Earth. This finding paves the way toward an efficient PP monitoring tool based on an SSFAC index derived from vector magnetic field observations at low-Earth orbit.
Keywords. Magnetospheric physics (plasmasphere)
The plasmasphere is a torus of cold (∼ 1 eV) plasma frozen into the Earth's magnetic field and co-rotating (e.g. Carpenter and Anderson, 1992) with the Earth. The plasmasphere is filled from the dayside ionosphere and emptied to the night side through ambipolar diffusion along field lines (e.g. Chiu et al., 1979; Sandel and Denton, 2007; Jorgensen et al., 2017). During geomagnetic disturbances the plasmasphere shrinks due to the increased global magnetospheric convection (e.g. Carpenter and Anderson, 1992; O'Brien and Moldwin, 2003), and the plasma of the outer shells is removed by medium-scale electric fields that drive plumes toward the magnetopause (e.g. Goldstein et al., 2003a; Moldwin et al., 2004; Darrouzet et al., 2008). The erosion processes take place dominantly on the night side. The eroded region appears hours later on the dayside as a consequence of co-rotation (e.g. Pierrard and Voiculescu, 2011; Katus et al., 2015; Zhang et al., 2017). Decreased convection and dayside refilling both play a role in the gradual expansion of the plasmasphere at quiet times, especially during the recovery phase of geomagnetic storms until the plasmasphere is saturated (e.g. Jorgensen et al., 2017). Hence, the shape of the plasmasphere depends more on the time history of geomagnetic activity (characterized e.g. by the Kp index) than on the concurrent disturbance level. Most of the previous modelling efforts have taken the memory effect of the plasmapause (PP) into account by comparing its position with the maximum Kp taken from an interval preceding the time considered (e.g. O'Brien and Moldwin, 2003). The length of the considered interval varies in the different models from a few hours to a few days. The end of the interval is typically a few hours before the model time. Recently, following the recommendation of Larsen et al. (2007), investigations of the PP response time take care of its MLT dependence (Katus et al., 2015; Zhang et al., 2017).
The plasmapause is conventionally defined as the innermost sharp gradient in equatorial plasma density, e.g. a factor of 5 drop in density within 0.5 RE (e.g. Carpenter and Anderson, 1992; O'Brien and Moldwin, 2003; Larsen et al., 2007; Zhang et al., 2017), a sharp edge in extreme ultraviolet (EUV) images of the He+ plasma line intensity around the Earth taken by the IMAGE satellite (Goldstein et al., 2003b), or as an iso-surface at some density threshold value (e.g. Chappell, 1974). Both in situ observations and remote-sensing techniques are applied to obtain information on plasma density or on the location of the plasmapause. Remote-sensing techniques include electron density observations inferred from the dispersion of very low-frequency (VLF) whistlers observed on the ground (e.g. Lichtenberger et al., 2013), plasma mass density estimations from the ultra low-frequency (ULF) eigenfrequencies of geomagnetic field lines (Menk and Waters, 2013), the detection of PP related boundaries in the topside total electron content (TEC) making use of dual frequency GPS receivers (Pedatella and Larson, 2010), locating the mid-latitude ionospheric trough (MIT) (Grebowsky et al., 1976; Yizengaw et al., 2005) as well as the ionospheric light ion trough (LIT) (e.g. Anderson et al., 2008), and other techniques beyond the already mentioned EUV imaging.
Recently a new PP detection technique was proposed by Heilig and Lühr (2013) utilizing the magnetic signatures of small-scale field-aligned currents (SSFACs) validated by in situ night-side PP detections of the IMAGE RPI (radio plasma imager) instrument (Reinisch et al., 2000). Hence the equatorward boundary of SSFACs can be considered as a proxy for the night-side PP location. We call this proxy the SSFAC index. In this paper we derive the SSFAC indices from the field-aligned current (FAC) observations of ESA's Swarm satellites. The SSFAC index is validated using PP positions calculated from in situ electron density observations of NASA's Van Allen Probes (VAPs). Furthermore, we extend the validation involving VAP data from all MLTs.
The paper is organized as follows. First, the derivation of the SSFAC index from Swarm data is reviewed. In Sect. 2 the Swarm observations are presented along with some statistics, including the investigation of the connection between the SSFAC index and some geomagnetic indices, as well as interplanetary parameters. Afterwards in Sect. 3 an empirical climatological model of the SSFAC boundary is introduced, before in Sect. 4 the validation results are presented. Results are discussed in Sect. 5; finally, we summarize our findings and draw conclusions.
The three Swarm satellites were launched into a polar low-Earth orbit (LEO) on 22 November 2013. During the commissioning phase the three satellites flew on the same orbit, following each other with an increasing separation. Since 17 April 2014 Swarm A and C have orbited side-by-side (1.4∘ east–west separation) at 460 km altitude and an inclination of 87.4∘, while Swarm B orbits at 510 km altitude and an inclination of 87.8∘. The orbital planes of Swarm B relative to A and C drift away slowly (by 5–6 min day−1) in magnetic local time (MLT) due to the different inclinations. In this study we utilized the FAC data derived from vector magnetic field data recorded by the fluxgate magnetometers with a resolution of 10 pT between 1 January 2014 and 31 December 2017. By the end of the investigated interval the MLT separation between Swarm A and B increased to ∼ 6 h. For inter-satellite comparisons Swarm A is preferred over Swarm C in this study, since the absolute scalar magnetometer instrument on the latter stopped working on 5 November 2014, resulting in a somewhat poorer calibration. However, we found no significant difference in the performance of Swarm A and C in monitoring the plasmapause.
Our plasmapause detection method is based on the localization of the equatorward boundary of SSFAC activity deduced from the transverse toroidal component of the geomagnetic field fluctuations observed at LEO. This new tool, which yields unprecedented details on the dynamic behaviour of the plasmapause, was first introduced and described in detail by Heilig and Lühr (2013).
For validation purposes we used in situ plasma density data. The twin (A and B) VAP spacecraft were launched on 30 August 2012 into a highly elliptical (with perigee at 700 km, apogee at 5.8 RE, orbital period ∼ 9 h), low inclination orbit with the primary objective of studying the Earth's Van Allen radiation belts. The in situ electron density data used in this study are inferred from the upper hybrid resonance frequency fuh observations by the plasma wave High Frequency Receiver (Waves HFR) instrument of the Electric and Magnetic Field Instrument Suite and Integrated Science (EMFISIS) suite. We used the electron number densities Ne observed between 1 January 2014 and 1 July 2016 by VAP A as derived by Zhelavskaya et al. (2016) through the Neural-network-based Upper hybrid Resonance Determination (NURD) algorithm. These in situ electron density data are openly available at the ftp://rbm.epss.ucla.edu/ftpdisk1/NURD/ ftp site. The NURD dataset includes L and geomagnetic latitude Λ along with density values. The spatial resolution in L ranges from a few 0.0001 RE at low L to a few 0.001 RE at high L. At such a narrow spacing the measurement error can easily exceed the true change rates, making the calculated density gradients very noisy. In order to decrease this effect, density profiles were filtered by applying a 31-point moving average. The length of the filter corresponds to L-value ranges of 0.001–0.1 RE, long enough to sufficiently depress the noise, but short enough not to affect the location of the PP associated density gradient significantly. After filtering, density profiles were down-sampled at dL = 0.01 RE resolution. From the resampled density values we determined orbit-by-orbit the PP position as the earthward edge of the innermost density gradient exceeding a factor of 5 drop within dL = 0.25 RE. We note that the gradient threshold we applied is twice as large as those applied by previous authors, simply because we found that the old (lower) threshold in many cases identifies the PP inward from the clear sharpest drops. This difference stems from the different spatial resolution between old and new data. The lower resolution of data from previous missions heavily smoothed the density profiles, necessitating the use of a lower threshold for PP detection. For better consistency with earlier data, we also calculated the neighbourhood of the previously described innermost sharp gradient, where the density gradient exceeds a factor of 5 drop within dL = 0.5 RE, i.e. the traditional threshold. The lower limit of this interval is then chosen as the location of the PP.
We also note that the VAP PP positions were derived from in situ density observations made at low latitudes. Since the detection relies on relative changes across L-shells, there is no significant impact of this choice on the results. This can be easily seen by combining the field-aligned distribution of plasmaspheric electron density , where Ne0 is the equatorial density, r0 is the radial distance of the equatorial point of the field line, r is the radial distance (Denton et al., 2006), and the equation of a dipole field line is r=r0cos 2Λ. From these we get for the ratio of the densities at two points along the field line. In the vicinity of the geomagnetic equator ( for closely separated (ΔΛ < 3∘) points, this formula yields only a few percent difference in Ne that is negligible compared to the factor of 5 drop we look for. Hereafter, VAP observed PP will be referred to as PP_Ne to distinguish them from the SSFAC index derived from Swarm FAC observations.
The main steps of data processing applied to Swarm observations are as follows. First, the field-aligned current (FAC) density, , available as the Swarm Level 2 product FACxTMS_2F (where x stands for A, B or C identifying the satellite) for each satellite individually, is high-pass filtered by a third-order Butterworth with a −3 dB cut-off at 250 mHz. The chosen cut-off frequency ensuring precise boundary localization corresponds to a ∼ 30 km spatial scale along the (quasi-meridional) orbit. Then the logarithm of the squared SSFAC density (in units µA m−2) is taken, and a boxcar averaging is applied to derive the SSFAC power level, S, subsequently used as a detection signal:
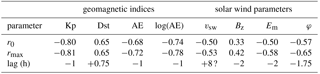
The detection of the SSFAC inner (equatorward) boundary is a multistep process. As a first step, each orbit is divided into four orbital segments including data from the magnetic equator to the poles. Then all segments are scanned for the innermost transition of S between two pre-defined reference levels (an increase in S from to . The applied reference values are found typically only inside/outside the nominal plasmapause (here the nominal plasmapause locations are derived from the Kp-based model of O'Brien and Moldwin, 2003). The L-values related to the corresponding S reference levels are denoted by Lc and Lm, respectively, where the L-value is calculated from the modified apex magnetic latitude assuming a dipole field geometry (, where rref≈1.02 is the geocentric distance of the E-region as reference height (110 km) in Earth's radii (6371.2 km). In the next step the change in the SSFAC power level within the transition zone [Lc; Lm] is represented by a linear fit, , and σ, the RMS value of the residuals ( in the [Lc; Lm] interval, is calculated. The width of the boundary dL is defined as Lc−Lm. Finally, the L-value where S∗ equals a threshold reference level, (∼ −4.0), is taken as the position of the boundary, Lssfac. Whenever Lssfac lies outside the interval [Lc; Lm], it is rejected. This typically happens when the boundary is not well defined, mostly on the dayside. The resulting detection of the equatorward boundary of intense SSFACs (the SSFAC index) is related to the L-value of the plasmapause in units of Earth radii (RE). The fit quality parameters, dL (the boundary width) and σ (characterizing the quality of the fit), are used to exclude less-defined transitions similarly as described in Heilig and Lühr (2013). The detection parameters (reference levels) applied at Swarm data analysis, and for comparison also for CHAMP, are given in Table 1.
To optimize the quality of the detection results, a fine adjustment of the reference value is needed. Following Heilig and Lühr (2013) we did it by maximizing the absolute correlation strength between the boundary position, Lssfac, and the geomagnetic index Kp. Allowing for comparisons on shorter timescales than the 3 h cadence of Kp, the Kp index was linearly interpolated at UTs of the SSFAC index. The best correlation was found at −4.1 (corresponding to ∼ 0.01 µA m−2 SSFAC density), very close to the value found for CHAMP (Table 1, Fig. 1b). During this and further calculations, Kp was delayed in time by 1 h. This value is inferred from a cross-correlation analysis between Kp and Lssfac (Fig. 1a), and corresponds to the mean response time of the boundary to changes in geomagnetic activity.
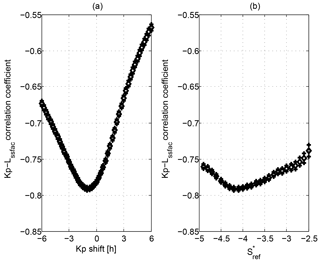
Figure 1(a) Lssfac–Kp cross-correlation, and (b) correlation between Lssfac and Kp as a function of the reference level .
To check whether the SSFAC boundary behaves similarly as the PP_Ne does, we investigated how the SSFAC index depends on the time history of Kp. For the correlation analysis, we determined the peak Kp in an x hour (x varies from 0 to 12 h) long interval ending y hours before (y varies from −6 to 2 h at 0.5 h steps) the investigated event, i.e. if the event time is depicted by t0, the considered interval is []. The SSFAC indices (Lssfac boundary positions) are correlated with the interval peak Kps. The result of this analysis is summarized in Fig. 2a and b. The individual columns of these figures can be read as cross-correlations between the SSFAC index and Kpmax as a function of the interval length.
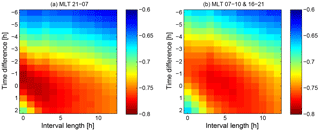
Figure 2Correlation strength between the SSFAC index and the peak Kp as a function of the length of the interval (horizontal axis), where the peak Kp is taken from the time difference (vertical axis) between the end of the interval and SSFAC index observation (a) in the sector (MLT 21:00–07:00), and (b) for morning (MLT: 07:00–10:00) and evening (MLT: 16:00—21:00) hours.
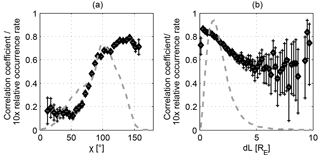
Figure 3(a) Dependence of the Lssfac–Kp correlation on the solar zenith angle “χ” while “dL” < 3 (diamonds) with 95 % confidence intervals (vertical lines) along with 10 times the relative occurrence rate of “χ” values (dashed line), and (b) the same correlation/occurrence rates in the same format as in (a) but as a function of the boundary width “dL” while χ > 90∘.
Similar correlation matrices were calculated separately for all the 24:00 MLT sectors (0..1, 1..2, 2..3, etc., not shown). We identified two distinct behaviours. On the night side (21:00–07:00 MLT) the response of the boundary is slightly faster than on the morning and dusk (07:00–10:00 and 16:00–21:00 MLT) sides. The variation of the boundary positions follows quite tightly any changes in Kp, with an average response time of 0.5–1 h (i.e. time difference or lag is between −0.5 and −1 h) in both Fig. 2a (night side case: 21:00–07:00 MLT) and b (07:00–10:00 and 16:00–21:00 MLT). Positive lag is unphysical and can be attributed to the low (3 h) time resolution of Kp. The interval length yielding the strongest correlation (deepest red) depends on the lag. The absolute maximum on the night side/dayside is found at −1/−1 h lag and 0/3–4 h interval length, respectively, meaning that the SSFAC index is dependent mainly on the latest/latest two values of Kp. Nighttime response is practically immediate, and even on the dayside the memory of the SSFAC index does not exceed a few hours.
The observation that the ∼ 1 h response time does not seem to depend on MLT can be interpreted as a synchronous response of the whole boundary to changes in geomagnetic activity. It means that the behaviour of the SSFAC index is different from that of the PP_Ne, which shows a local time dependent response time to magnetic activity (Katus et al., 2015; Zhang et al., 2017).
The correlation strength between the SSFAC index and Kp was found by Heilig and Lühr (2013) to vary with MLT, solar zenith angle χ, and the fit quality parameters. We repeated this analysis with Swarm data and the results confirm our previous findings: the correlation is stronger than 0.6 during nighttime conditions (χ > 90∘) (Fig. 3a) or between 18:00 and 06:00 MLT. On the dayside, the detection of the boundary is disturbed by other phenomena, such as shear Alfvén waves including geomagnetic field line resonances (Heilig et al., 2013). As another example, Fig. 3b clearly presents the decrease in the correlation strength with increasing boundary width, dL. The correlation is stronger than 0.65 for steeper slopes (“a” > 0.5 or dL < 3) on the night side. This finding suggests that the boundary can be detected easier and more accurately, when the boundary is sharper. This happens, as we will see, during increased geomagnetic activity.
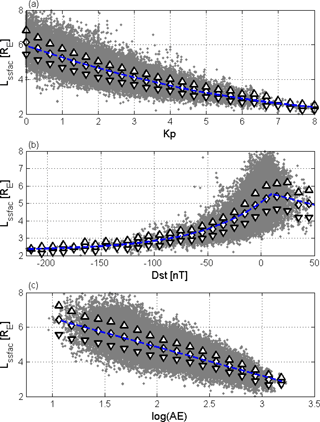
In the following, based on the above and previous (Heilig and Lühr, 2013) findings, our statistical analysis of the SSFAC index is restricted to sharp (dL < 3) boundary transitions observed at solar zenith angles χ greater than 90∘ and between 18:00 and 06:00 MLT. These conditions reduce the overall 242 317 boundary crossings to 84 010 (35 % of all crossings). Outliers standing out more than 0.5 RE from the five-point running mean are then removed, reducing further the event number to 68 344 suitable observations (28 % of all crossings). For the different magnetic activity indices Kp, Dst, AE, and log(AE) the cross-correlation maximizes at rmax for the lag times: −0.81 at −1 h lag (Fig. 4a), 0.65 at +0.75 h lag (Fig. 4b), −0.72 at −1 h lag, and −0.78 at −1 h lag (Fig. 4c), respectively (see Table 2 for a summary). This confirms that Kp describes best the average behaviour and the dynamics of the boundary. That is why we used Kp for deriving an empirical model. However, it is still worth having a closer look at the dependences of all the indices.
The Kp dependence (time-shifted) can be approximated quite well by a simple ratic function (Fig. 4a, Eq. 2), similar to that of Heilig and Lühr (2013):
In Fig. 4a, and also in the following plots, triangles depict the mean ± standard deviation values. The correlation strength between the observations and the Kp-based model is 0.81. As Fig. 4b shows, unlike the Kp dependence, the Dst index does not influence the SSFAC index evenly over its full range, mainly when Dst is negative, i.e. during the storm-time intensified ring current. For these values Eq. (3) presents an exponential fit accounting for the dependence. At the same time, positive Dst values typically occurring during the initial phase of geomagnetic storms as a consequence of the magnetopause current increase do not seem to have a strong impact. A possible reason is that while the ring current is involved in the processes forming the new PP, the magnetopause current does not.
The relation to the AE index is shown in Fig. 4c. An improved linear dependence of the SSFAC index location was found for log(AE) (Eq. 4). Unlike the Dst, a monotone dependence extends over the full range of the AE index, indicating that auroral electrojets of any strength correlate with the SSFAC boundary position.
While the SSFAC boundary is observed both below L= 2 and beyond L= 8, none of the above index-based models can account for the whole range of variations. The output of the Kp-based model ranges from L= 2.3 (Kp = 9) to L= 6.0 (Kp = 0). The Dst-based model estimates vary between L= 2.3 (Dst = −500 nT) and L= 5.7 (Dst = 10 nT), while the AE model yields values between L= 2.9 (AE = 1600 nT) and L= 6.5 (AE = 10 nT). In all three cases the range of L variation accounted for by the model is nearly the same, ΔL= 3.5; however, the baselines are different. The Dst/AE-based model is capable of accounting for the lowest/highest extremes, respectively. From the stronger correlation and the 1 h response time it seems that the AE index (strength of the auroral electrojet) reflects more closely the processes that form the SSFAC boundary than the Dst index. At the same time, large Dst indices (developed ring current) tend to be concomitant with the inward motion of the SSFAC boundary below the Lssfac=3 limit. Indeed, during intense storms, when , Lssfac stays below 3 RE.
Since the geomagnetic activity is driven by Sun–Earth interactions, and the plasmapause location is controlled to first approximation by the magnetospheric convection, it is not surprising that there is a link between the SSFAC equatorward boundary and some interplanetary parameters accounting for the solar-wind–magnetosphere coupling, as well. We found a negative correlation (Table 2) with the solar wind speed (vsw), a weak positive correlation with the IMF GSM southward component (Bz), and again negative correlations with two solar-wind–magnetospheric coupling parameters: the merging electric field (Kan and Lee, 1979) , and the coupling parameter suggested by Larsen et al. (2007). Here Bt ∕ B is the IMF component perpendicular to the Sun–Earth line/the total IMF, respectively, and θ is the clock angle, i.e. the angle between Bt and Bz. Although the merging proxies give higher coefficients (−0.58 and −0.65), these are still weaker than the correlations with geomagnetic indices. Moreover, the time lags are typically 2 h, twice as large as for the Kp and AE indices. These are likely because of the less direct link between the SSFAC boundary dynamics and the solar wind conditions, compared to the more direct impact of the auroral dynamics and the ring current. We note here that the positive time lag found for solar wind speed is unphysical and was neglected during further analysis. Solar wind speed mostly changes on longer timescales than plasmasphere dynamics and that is why the cross-correlation peak is rather flat, as can be seen from the similar correlation strength at +8 h (−0.53) and at 0 h time lag (−0.50) in Table 2. This makes the determination of the response time less reliable.
The nature of the dependence of the boundary location on the considered four solar wind parameters can be seen in Fig. 5a–d. Functional dependences are given by Eqs. (5) to (8). As shown in Fig. 5b, Bz has a significant influence only when it is southward (negative), i.e. when dayside IMF-geomagnetic field line merging takes place, a process that drives magnetospheric convection. The merging electric field Em and the coupling parameter φ are even more directly linked to magnetospheric convection. It is known that the convection plays a crucial role in the formation of the plasmapause. Whenever the convection increases, the plasmasphere shrinks.
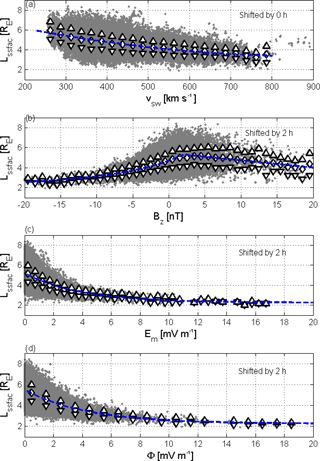
Figure 5Dependence of the SSFAC index on the (a) solar wind speed, (b) Bz IMF south GSM component, (c) merging electric field, and (d) coupling parameter φ.
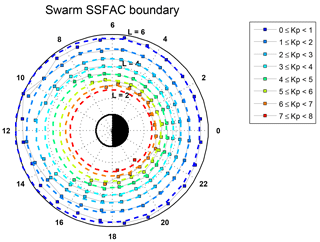
Before starting to discuss the dynamics of the plasmapause we have a detailed look at the small-scale FAC boundary. In Fig. 6 the mean L-values of the SSFAC inner boundary calculated from all observations between 1 January 2014 and 31 December 2017 from all three Swarm satellites are presented on a dial plot as a function of MLT. Individual circles are drawn for different levels of geomagnetic activity (, , , etc.), while the polar histogram in the bottom right presents the MLT distribution of the sample numbers. Only the mean positions of the boundary are shown, where at least 10 observations are available. For the above-mentioned reasons, the detection is restricted to times when χ > 90∘, causing the asymmetric day–night MLT distribution of detections (see histogram). This is also the main reason for the dayside gap in the boundary determination, especially at high Kp.
The shape of the boundary in Fig. 6 closely resembles a circle in L versus MLT space for any level of geomagnetic activity. The radius of the circle scales inversely with Kp. The circles are not exactly geocentric, and the centres are slightly shifted toward noon. The standard deviation of the individual Lssfac observations is also a clear function of Kp, decreasing from ∼0.7 RE at Kp = 0 to ∼0.2 RE at Kp = 7; however, it hardly depends on MLT. The uncertainty of the means (SD ∕ sqrt(N)) is 0.01–0.02 RE at each Kp level.
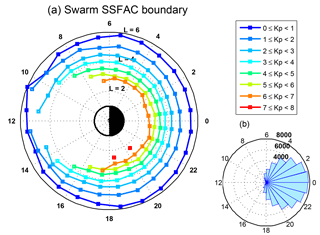
Figure 6(a) Mean boundary positions as a function of MLT at different levels of Kp (0–1, 1–2, 2–3, 3–4, 4–5, 5–6, 6–7, 7–8) and (b) the MLT distribution of the boundary crossings.
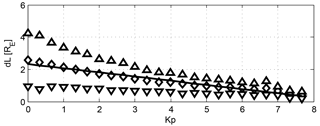
Not only the boundary position, but also the boundary width, is a function of Kp. The boundary gets narrower when geomagnetic activity increases, as shown in Fig. 7. At low activity, the mean width is around 2.5 RE, but the scatter is large, while for Kp > 6 the boundary becomes narrower than 1 RE. The overwhelming majority of the boundary observations are made at relatively sharp boundaries, i.e. when the boundary width is lower than 3 RE (see Fig. 3b). As stated before, in our statistical analysis only these sharper boundaries were considered.
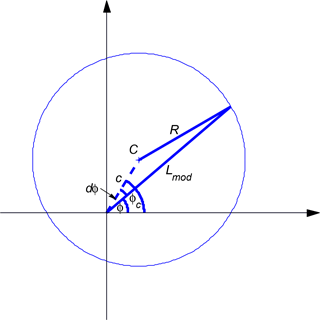
For a given level of Kp, we model the observed boundary in L space by an eccentric circle. The position of a point P on the circle is given by its polar coordinates Lmod and as shown in Fig. 8. If the circle is centred at C(c,φc) and has a radius R, Lmod can be derived for any MLT by applying the formula
where d and 360∘.
Moreover, we suppose that the position of C and the radius of the circle R have a linear/ratic dependence on Kp, respectively, that is
where c0 and MLT0 define the position of the centre and R0 is the radius of the circle, both at Kp=0, while p1, p2, γc, γmlt are free model parameters. Based on 68344 boundary positions observed during the period 1 January 2014–31 December 2017, the following model parameters (with 95 % confidence bounds) were obtained:
The corresponding model is presented in Fig. 9 as dashed circular curves. The centres of the circulars hardly move with increasing Kp. From Kp = 0 to Kp = 6, it moves from MLTc= 12.2, c= 0.3 RE to MLTc= 13.4, c=0.1 RE. The mean residuals (observation–model) in each bin are between −0.3 and 0.2 RE at all Kp levels between 1 and 6. At Kp = 0 the mean residuals are in the range −0.6–0.2 RE.
Any of the three Swarm satellites visits all the MLT sectors during every 132-day period. Five full years of data are needed for an even coverage of local time during all seasons. Since we consider only 4 years, our model might suffer from a seasonal bias. We found, however, that the seasonal variation is small (±0.13 RE or ±3 %) and dominantly caused by the varying geomagnetic conditions (not shown). Therefore no significant improvements in seasonal specification are expected by considering slightly longer datasets from Swarm.
4.1 Extension of Lssfac observed at some MLT to any other MLT
The model derived in the previous section can be used in various ways. First, it can be used as a climatology model. When no boundary observations are available, Lmod can be calculated directly from MLT and Kp as inputs. However, if we have an observation of Lssfac=Lobs at a certain MLTobs and the geomagnetic activity given by the Kp index is known, we can, by combining the model (yielding the shape and the centre of the boundary) with the actual observation (providing the actual radius), estimate Lssfac at any other MLT. This is done by rescaling the size of the boundary based on the actual observation, while taking the average circular shape and Kp-dependent centre position from the model:
Since the Kp dependence of both c and MLTc is found to be very weak, we can regard them as constant, e.g. 12 h, while d can be calculated from the model. This will cause less than 0.05 RE error. Now Lmod at any MLT can be computed by the direct use of Eq. (9), but substituting R′ into R.
We verified our SSFAC index estimates by checking the consistency between the observations of the different satellites. By using the model and Swarm B observations we estimated the boundary locations at the MLT of Swarm A (LAB) and compared the calculated positions with the actual Swarm A (LA) observations at that MLT. The UT difference of the boundary crossing between the original Swarm A and B observations was limited to 15 min. The result of this comparison is shown in Fig. 10. A large range of L-values (from 2 to 8 Re) is covered. Predicted and observed values were found to be close to each other; see Eq. (12).
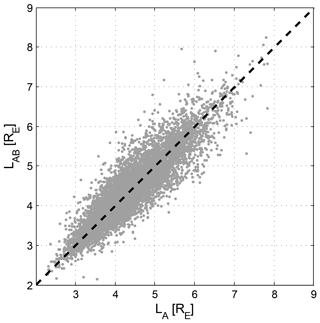
Figure 10Comparison of Swarm A SSFAC indices with indices predicted from simultaneous Swarm B observations.
In 90 % of all these cases their absolute difference was less than 0.59 RE. It implies that at least for the MLT separation limited so far (0 to 6 h) between the spacecraft, the boundary can be well approximated by a circle not only on average, but also at any given moment. This behaviour is different from that of the plasmapause, which – due to the co-rotation of the plasmasphere with the Earth – has a memory of the Kp time history: i.e. the plasmapause position at some later MLT on the dayside depends more on the preceding Kp-values than on the actual Kp. Furthermore, this result also confirms our previous finding that the SSFAC boundary responds nearly simultaneously at all MLT. It directly follows from its constant circular shape.
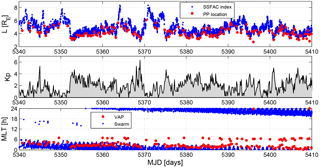
The SSFAC equatorward boundary was proposed as a proxy for the PP distance by Heilig and Lühr (2013). They validated their proxy by comparing it to in situ PP_Ne observations derived from electron density observations of the Radio Plasma Imager instrument onboard the IMAGE satellite. They found an excellent agreement between the two boundaries near MLT midnight. The PP_Ne is located inward of the SSFAC boundary on average by 0.4 RE. Making use of the high quality, high resolution VAP density observations, we repeated this comparison. In the top panel of Fig. 11 the SSFAC index observations of all three Swarm spacecraft (blue) and in situ PP_Ne observations of VAP A (red) for a 69-day long period (15 August–24 October 2014) are shown. Although the SSFAC index varied roughly between L= 3 and 8 in the time interval considered, the comparison is limited to the L= 2–6 range, due to the orbit apogee of VAP. The variation of the SSFAC index follows very closely the PP_Ne variation. There are only two outliers of VAP observations in the whole interval. The other important thing to note is that Swarm observations yield a much more detailed and higher resolution picture of the boundary time evolution. They resolve both fast expansion (e.g. modified Julian days (MJDs) 5363 and 5370) and rapid contraction (MJD 5352) (MJD: daynumber since 1 January 2000, 00:00 UT), and reflect well shorter-scale Kp variations (middle panel). Our method offers an unprecedented monitoring tool to study plasmasphere dynamics.
However, the correspondence is not always as perfect as in the above example, only when the VAP validation dataset is taken from the post-midnight MLT sector (00:00–07:00 MLT; see bottom panel). The MLT of the Swarm observations is less important since the SSFAC boundary is circular and the offset of its centre from the Earth's centre is small. Comparison with VAP PP_Ne observations made at other MLTs gives a different result. The plasmasphere is well known for having a dusk-side bulge and its distance at different MLTs can be quite different, controlled by the past variation of magnetospheric convection. By contrast, the SSFAC boundary responds almost simultaneously at all MLTs (within about an hour) to changing conditions. The two boundaries are coupled only near midnight and in the early morning sector.
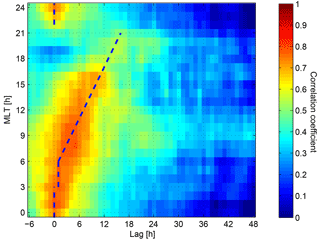
To confirm this, we calculated the cross-correlation between the two boundaries. First, for each VAP PP_Ne position we calculated the mean of all available SSFAC indices from the Swarm spacecraft within ±1 h UT difference. Then the correlation between the two time series was calculated separately for each 4 h long MLT interval centred at integer MLT hours. Then the calculation was repeated with a time-shifted SSFAC index time series. The time shift varied from −6 to 48 h. The result is shown in Fig. 12. The maximum correlation is at 0–1 h lag from 22:00 to 06:00 h, while after 06:00 MLT, the lag increases more or less linearly with increasing MLT (marked by the overplotted slant dashed lines). We interpret this result as follows. Between 22:00 and 06:00 MLT the PP_Ne's response is relatively fast and nearly simultaneous to changes in the SSFAC index. This MLT sector is expected to be the region where the PP is formed. From about 06:00 to 18:00 MLT (and beyond) the MLT-dependent linear increase of the time lag (with slope 1/1 h) can be interpreted as a consequence of the co-rotation of the plasmasphere with the Earth, i.e. the plasmapause formed on the nightside propagates by co-rotation into the daytime sector. Between 17:00 and 21:00 MLT, where the PP_Ne typically has a bulge, the correlation is the weakest. It seems that the memory of the PP_Ne is longer in the morning and near dusk hours. There may be a secondary peak at around 24 h time lag; however, this is not very clear from the present data. It might also be the tail of an elongated peak. We extended this calculation up to 72 h time lag (not shown), but we could not identify further clear peaks.
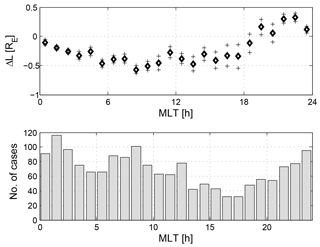
We also estimated the mean separation between the boundaries as a function of MLT from 1665 Swarm crossings (Fig. 13). SSFAC indices and simultaneous (UT difference is less than ±1 h) VAP PP_Ne positions were compared. The comparison revealed a clear bulge signature in the pre-midnight sector (19:00–01:00 MLT) peaking at 21:00–22:00 MLT. Elsewhere the SSFAC boundary is found typically poleward of the PP by ∼ 0.2 R. This result is very similar to the obtained differences between CHAMP and IMAGE observations. However, for individual cases the location of the boundaries can be very different. While the PP_Ne shape, due to its co-rotation with Earth and the localized erosion, is determined by the Kp evolution in the preceding days, the SSFAC index responds within a few hours simultaneously at all MLTs. This difference has important implications for the derivation of a future PP model that is based on SSFAC boundary detections.
From our results it is clear that the PP_Ne does not follow closely the SSFAC boundary. The shape of the latter corresponds more to an equatorial cut of a drift shell, and soft electrons may precipitate from this drift shell into the ionosphere. Precipitation enhances the conductance of the ionosphere, leading to increased current density. Indeed, Xiong and Lühr (2014) derived a model of the auroral oval boundaries from SSFAC signatures observed at LEO. Their equatorward boundary defined as the highest poleward gradient in log squared SSFAC density equatorward of the maximum is consistently poleward of our SSFAC boundary; since our fixed threshold is low, at 0.01 µA m−2, the mean FAC density at their boundary is more than an order of magnitude higher. The PP typically maps to the sub-auroral ionosphere, where the conductance is smaller than in the auroral oval. Moving poleward from low latitudes, the first SSFACs appear just outside the PP_Ne. We believe that this is the reason why the SSFAC boundary is collocated with the night side PP_Ne under quiet conditions. Our plan for the future is to investigate the dynamic linkage among the elements of this complex system.
We compared the location of the equatorial boundary of the occurrence of SSFACs derived from magnetic field signature observed at LEO by the three Swarm satellites, and the PP_Ne obtained from in situ plasma density observations. We confirmed previous findings of Heilig and Lühr (2013), namely that the two boundaries are not identical, but tightly coupled from pre-midnight to dawn with a correlation coefficient of above 0.7, and closely located. On average the SSFAC boundary appears on larger L-values than the PP_Ne by ∼ 0.2 RE, except for the bulge region. While the PP_Ne forms a bulge near dusk, the SSFCAC boundary is circular at any level of geomagnetic activity with a radius decreasing with increasing geomagnetic activity (Kp). Furthermore, we found that the SSFAC boundary responds nearly simultaneously at all MLTs within an hour, while the PP_Ne response time has a known dependence on MLT, i.e. the response time increases on the dayside with MLT. We confirmed this behaviour by estimating the lag at the maximum cross-correlation between the PP_Ne location and the SSFAC boundary. The PP_Ne position correlates at some MLT sectors with the time history of the SSFAC boundary, and consequently with the dynamic processes that form the new PP_Ne around the midnight sector. The SSFAC index observed at any MLT can be used as a proxy for the location of the night side (22:00–06:00 MLT) PP. A midnight PP index as a proxy for the midnight PP position can be derived by reducing all SSFAC indices to MLT = 0 h by applying the procedure described in Sect. 3.1. Moreover, daytime PP_Ne location can be estimated from past SSFAC indices taking into account the co-rotation time passed since the formation of the new PP on the night side. This way the PP shape can be reconstructed from the past SSFAC indices. LEO satellites with high quality magnetic data provide a unique, efficient, and robust tool to monitor the dynamics of the PP. It can be used as a near-real-time monitoring tool in case magnetic data from LEO satellites are available.
Swarm FAC data are available through the ESA Earth Online platform, after registration for an ESA Earth Observation Users' Single Sign On account https://earth.esa.int/web/guest/ umsso?orig_request=/web/guest/picommunity/myearthnet (ESA, 2018). VAP electron density data are openly available at the ftp site of the Space Environment Modeling Group at UCLA (ftp://rbm.epss.ucla.edu/ftpdisk1/NURD/) (UCLA, 2016). Geomagnetic indices (Kp, Dst, AE) and the solar wind data were retrieved through the NASA OMNIWeb space physics data facility at http://omniweb.gsfc.nasa.gov/ (GSFC, 2018).
The authors declare that they have no conflict of interest.
This article is part of the special issue “Dynamics and interaction of processes in the Earth and its space environment: the perspective from low Earth orbiting satellites and beyond”. It is not associated with a conference.
We are grateful to Yuri Shprits for fruitful scientific discussions and for
providing the VAP NURD electron density dataset. We thank ESA for providing
Swarm Level 1b magnetic field data through project SSVO 2011 no. 10242
(PI : BH) and for Swarm Level 2 product FACxTMS_2F. We acknowledge the
use of the NASA/GSFC's Space Physics Data Facility's ftp service providing
OMNI data. Balázs Heilig is funded by the Government of Hungary through
an ESA contract under PECS (Plan for European Cooperating States) no.
4000114839/15/NL/NDe and the Bolyai Scholarship of the Hungarian Academy of
Sciences. This study was performed as part of ESA-funded project “P2-SWE-XVI
– Swarm Utilization Analysis” contract no. 4000117636/16/D/MRP and by DFG
Priority Programme “DynamicEarth”, SPP-1788.
The article processing charges for this open-access
publication were covered by a Research
Centre of the
Helmholtz Association.
The topical editor,
Claudia Stolle, thanks two anonymous referees for help in evaluating this
paper.
Anderson, P. C., Johnston, W. R., and Goldstein, J.: Observations of the ionospheric projection of the plasmapause, Geophys. Res. Lett., 35, L15110, https://doi.org/10.1029/2008GL033978, 2008.
Carpenter, D. L. and Anderson, R. R.: An ISEE/whistler model of equatorial electron density in the magnetosphere, J. Geophys. Res., 97, 1097–1108, 1992.
Chappell, C. R.: Detached plasma regions in the magnetosphere, J. Geophys. Res., 79, 1861–1870, https://doi.org/10.1029/JA079i013p01861, 1974.
Chiu, Y. T., Luhmann, J. G., Ching, B. K., and Boucher Jr., D. J.: An equilibrium model of plasmaspheric composition and density, J. Geophys. Res., 84, 909–916, https://doi.org/10.1029/JA084iA03p00909, 1979.
Darrouzet, F., De Keyser, J., Décréau, P. M. E., El Lemdani-Mazouz, F., and Vallières, X.: Statistical analysis of plasmaspheric plumes with Cluster/WHISPER observations, Ann. Geophys., 26, 2403–2417, https://doi.org/10.5194/angeo-26-2403-2008, 2008.
Denton, R. E., Takahashi, K., Galkin, I. A., Nsumei, P. A., Huang, X., Reinisch, B. W., Anderson, R. R., Sleeper, M. K., and Hughes, W. J.: Distribution of density along magnetospheric field lines, J. Geophys. Res., 111, A04213, https://doi.org/10.1029/2005JA011414, 2006.
ESA: Swarm FAC data, available at: https://earth.esa.int/web/guest/ umsso?orig_request=/web/guest/picommunity/myearthnet, last access: 5 April 2018.
Goldstein, J., Sandel, B. R., Hairston, M. R., and Reiff, P. H.: Control of plasmaspheric dynamics by both convection and sub-auroral polarization stream, Geophys. Res. Lett., 30, 2243, https://doi.org/10.1029/2003GL018390, 2003a.
Goldstein, J., Spasojević, M., Reiff, P. H., Sandel, B. R., Forrester, W. T., Gallagher, D. L., and Reinisch, B. W.: Identifying the plasmapause in IMAGE EUV data using IMAGE RPI in situ steep density gradients, J. Geophys. Res., 108, 1147, https://doi.org/10.1029/2002JA009475, 2003b.
Grebowsky, J. M., Maynard, N. C., Tulunay, Y. K., and Lanzerotti, L. J.: Coincident observations of ionosphere trough and the equatorial plasmapause, Planet. Space Sci., 24, 1177–1185, 1976.
GSFC: Geomagnetic indices (Kp, Dst, AE) and the solar wind data, available at: http://omniweb.gsfc.nasa.gov/, last access: 5 April 2018.
Heilig, B. and Lühr, H.: New plasmapause model derived from CHAMP field-aligned current signatures, Ann. Geophys., 31, 529–539, https://doi.org/10.5194/angeo-31-529-2013, 2013.
Heilig, B., Sutcliffe, P. R., Ndiitwani, D. C., and Collier, A.: Statistical study of geomagnetic field line resonances observed by CHAMP and on the ground, J. Geophys. Res.-Space, 118, 1934–1947, https://doi.org/10.1002/jgra.50215, 2013.
Jorgensen, A. M., Heilig, B., Vellante, M., Lichtenberger, J., Reda, J., Valach, F., and Mandic, I.: Comparing the Dynamic Global Core Plasma Model with ground-based plasma mass density observations, J. Geophys. Res.-Space, 122, 7997–8013, https://doi.org/10.1002/2016JA023229, 2017.
Kan, J. K. and Lee, L. C.: Energy coupling function and solar wind-magnetosphere dynamo, Geophys. Res. Lett., 6, 577–580, 1979.
Katus, R. M., Gallagher, D. L., Liemohn, M. W., Keesee, A. M., and Sarno-Smith, L. K.: Statistical storm time examination of MLT-dependent plasmapause location derived from IMAGE EUV, J. Geophys. Res.-Space, 120, 5545–5559, https://doi.org/10.1002/2015JA021225, 2015.
Larsen, B. A., Klumpar, D. M., and Gurgiolo, C.: Correlation between plasmapause position and solar wind parameter, J. Atmos. Sol.-Terr. Phy., 69, 334–340, https://doi.org/10.1016/j.jastp.2006.06.017, 2007.
Lichtenberger, J., Clilverd, M., Heilig, B., Vellante, M., Manninen, J., Rodger, C., Collier, A., Jørgensen, A., Reda, J., Holzworth, R., and Friedel, R.: The plasmasphere during a space weather event: first results from the PLASMON project, J. Space Weather Space., 2013, A23, https://doi.org/10.1051/swsc/2013045, 2013.
Menk, F. W. and Waters, C. L.: Magnetoseismology: Ground-based Remote Sensing of Earth's Magnetosphere, Wiley, Weinheim, Germany, 244 pp., 2013.
Moldwin, M. B., Howard, J., Sanny, J., Bocchicchio, J. D., Rassoul, H. K., and, Anderson, R. R.: Plasmaspheric plumes: CRRES observations of enhanced density beyond the plasmapause, J. Geophys. Res., 109, A05202, https://doi.org/10.1029/2003JA010320, 2004.
O'Brien, T. P. and Moldwin, M. B.: Empirical plasmapause models from magnetic indices, Geophys. Res. Lett., 30, 1152, https://doi.org/10.1029/2002GL016007, 2003.
Pedatella, N. M. and Larson, K. M.: Routine determination of the plasmapause based on COSMIC GPS total electron content observations of the midlatitude trough, J. Geophys. Res., 115, A09301, https://doi.org/10.1029/2010JA015265, 2010.
Pierrard, V. and Voiculescu, M.: The 3D model of the plasmasphere coupled to the ionosphere, Geophys. Res. Lett., 38, L12104, https://doi.org/10.1029/2011GL047767, 2011.
Reinisch, B. W., Haines, D. M., Bibl, K., Cheney, G., Galkin, I. A., Huang, X., Myers, S. H., Sales, G. S., Benson, R. F., Fung, S. F., Green, J. L., Taylor, W. W. L., Bougeret, J.-L., Manning, R., Meyer-Vernet, N., and Moncuquet, D. M., Carpenter, L., Gallagher, D. L., and Reiff, P.: The Radio Plasma Imager investigation on the IMAGE spacecraft, Space Sci. Revi., IMAGE special issue, 91, 319–359, 2000.
Sandel, B. R. and Denton, M. H.: Global view of refilling of the plasmasphere, Geophys. Res. Lett., 34, L17102, https://doi.org/10.1029/2007GL030669, 2007.
UCLA: VAP electron density data, available at: ftp://rbm.epss.ucla.edu/ftpdisk1/NURD/, last access: 5 April 2018.
Xiong, C. and Lühr, H.: An empirical model of the auroral oval derived from CHAMP field-aligned current signatures – Part 2, Ann. Geophys., 32, 623–631, https://doi.org/10.5194/angeo-32-623-2014, 2014.
Yizengaw, E., Wei, H., Moldwin, M. B., Galvan, D., Mandrake, L., Mannucci, A., and Pi, X.: The correlation between mid-latitude trough and the plasmapause, Geophys. Res. Lett., 32, L10102, https://doi.org/10.1029/2005GL022954, 2005.
Zhang, X.-X., He, F., Lin, R.-L., Fok, M.-C., Katus, R. M., Liemohn, M. W., Gallagher, D. L., and Nakano, S.: A new solar wind-driven global dynamic plasmapause model: 1. Database and statistics, J. Geophys. Res.-Space, 122, 7153–7171, https://doi.org/10.1002/2017JA023912, 2017.
Zhelavskaya, I. S., Spasojevic, M., Shprits, Y. Y., and Kurth, W. S.: Automated determination of electron density from electric field measurements on the Van Allen Probes spacecraft, J. Geophys. Res.-Space, 121, 4611–4625, https://doi.org/10.1002/2015JA022132, 2016.
- Abstract
- Introduction
- Data and analysis
- Statistical dependence on geomagnetic and solar wind conditions
- An empirical model of the SSFAC inner boundary
- Validation of the SSFAC index
- Possible physical links between PP_Ne and the SSFAC index
- Summary and conclusions
- Data availability
- Competing interests
- Special issue statement
- Acknowledgements
- References
- Abstract
- Introduction
- Data and analysis
- Statistical dependence on geomagnetic and solar wind conditions
- An empirical model of the SSFAC inner boundary
- Validation of the SSFAC index
- Possible physical links between PP_Ne and the SSFAC index
- Summary and conclusions
- Data availability
- Competing interests
- Special issue statement
- Acknowledgements
- References