the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
An initial ULF wave index derived from 2 years of Swarm observations
Constantinos Papadimitriou
Ioannis A. Daglis
Omiros Giannakis
The ongoing Swarm satellite mission provides an opportunity for better knowledge of the near-Earth electromagnetic environment. Herein, we use a new methodological approach for the detection and classification of ultra low-frequency (ULF) wave events observed by Swarm based on an existing time-frequency analysis (TFA) tool and utilizing a state-of-the-art high-resolution magnetic field model and Swarm Level 2 products (i.e., field-aligned currents – FACs – and the Ionospheric Bubble Index – IBI). We present maps of the dependence of ULF wave power with magnetic latitude and magnetic local time (MLT) as well as geographic latitude and longitude from the three satellites at their different locations in low-Earth orbit (LEO) for a period spanning 2 years after the constellation's final configuration. We show that the inclusion of the Swarm single-spacecraft FAC product in our analysis eliminates all the wave activity at high altitudes, which is physically unrealistic. Moreover, we derive a Swarm orbit-by-orbit Pc3 wave (20–100 MHz) index for the topside ionosphere and compare its values with the corresponding variations of solar wind variables and geomagnetic activity indices. This is the first attempt, to our knowledge, to derive a ULF wave index from LEO satellite data. The technique can be potentially used to define a new Level 2 product from the mission, the Swarm ULF wave index, which would be suitable for space weather applications.
Keywords. Space plasma physics (waves and instabilities)
Please read the corrigendum first before continuing.
-
Notice on corrigendum
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
-
Article
(4171 KB)
-
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
- Article
(4171 KB) - Corrigendum
- BibTeX
- EndNote
Swarm is the fourth Earth Explorer mission of the European Space Agency (ESA), launched on 23 November 2013. The mission measures the geomagnetic field by identifying and measuring magnetic signals from the Earth's core, mantle, crust, oceans, ionosphere, and magnetosphere (Friis-Christensen et al., 2006). Additionally, Swarm data are used to study the Sun's influence on the Earth system by analyzing electric currents in the magnetosphere and ionosphere and understanding the impact of solar wind on the dynamics of the upper atmosphere. Swarm currently offers one of the best-ever surveys of the Earth's main and crustal magnetic field (Civet et al., 2015; De Michelis et al., 2015; Hulot et al., 2015; Olsen et al., 2015; Schnepf et al., 2015) as well as the near-Earth electromagnetic environment (Alken et al., 2015; Archer et al., 2015; Buchert et al., 2015; Dunlop et al., 2015; Goodwin et al., 2015; Iyemori et al., 2015; Lühr et al., 2015a, b; Park et al., 2015; Pitout et al., 2015; Spicher et al., 2015). The interested reader is also referred to the special issue “Swarm science results after 2 years in space” (for details, see Olsen et al., 2016). The final constellation of the three-satellite mission with two spacecraft (Swarm A and C) flying side by side at low altitude (∼ 460 km) and one (Swarm B) flying at a slightly higher altitude (∼ 510 km) was achieved on 17 April 2014.
Magnetospheric ultra low-frequency (ULF) waves in the topside ionosphere are typically transmitted from magnetospheric and upstream solar wind sources. Just as is the case for ULF waves observed on the ground, the amplitude of the waves in the topside ionosphere is significantly smaller than that of the background magnetic field. Observations in the topside ionosphere therefore require magnetometers that are both extremely sensitive (< 1 nT) and have a large dynamic range (±60 000 nT). ULF wave observations in the ionosphere were first reported in the late 80s during the MAGSAT era (Iyemori and Hayashi, 1989) when data from the mission were used to detect Pc1 waves (with frequency f ≃ 0.2–5 Hz). A number of magnetic and electric field missions flying in a low-Earth orbit (LEO), like CHAMP, Ørsted, SAC-C, or ST5, have enabled us to study in situ the occurrence of ULF waves in the topside ionosphere. In particular, ULF wave monitoring from LEO satellites has been most prominently reported in the Pc3 frequency range (f ≃ 20–100 MHz) (e.g., Jadhav et al., 2001; Vellante et al., 2004; Heilig et al., 2007, 2013; Ndiitwani and Sutcliffe, 2009; Le et al., 2011; Balasis et al., 2012, 2015a; Chi and Le, 2015; Yagova et al., 2015), while for Pc1 waves (e.g., Engebretson et al., 2008; Park et al., 2013a) and Pi2 waves (f ≃ 2–25 MHz) (e.g., Sutcliffe and Lühr, 2003) there have been fewer studies.
The CHAMP satellite has been one of the most successful missions for the study of the Earth's magnetic field, with high-sensitivity and accuracy magnetometer measurements orbiting within an altitude range of 450–300 km for more than a decade (July 2000–September 2010). For the first time long-term statistical studies on the occurrence of compressional Pc3 waves in the topside ionosphere were possible (Heilig et al., 2007). Recently, new features of Pc3 wave power in the topside ionosphere were revealed by Swarm observations based on 1 year of mission data (Balasis et al., 2015b). Moreover, Heilig and Sutcliffe (2016) used Swarm data to investigate the distribution of wave coherence and phase difference as functions of magnetic latitude and local time.
A satellite flying in a polar, low-Earth orbit is a suitable platform for observing ionospheric instabilities in the F-region like the post-sunset equatorial spread-F (ESF) events (Stolle et al., 2006). These instabilities are generally accompanied by local depletions of the electron density.
In this study, we present a new technique that combines a wavelet spectral analysis technique (Balasis et al., 2013), a state-of-the-art high-resolution magnetic field model (Finlay et al., 2016), and Swarm Level 2 products (i.e., field-aligned currents – FAC – and the Ionospheric Bubble Index – IBI) in order to study the occurrence and distribution of compressional Pc3 waves in the topside ionosphere based on Swarm observations for a time period spanning 2 years. We derive orbit-by-orbit (i.e., ∼ 1.5 h) variations of the Pc3 wave power, thus leading to the calculation of the Swarm ULF wave index for the topside ionosphere, and compare them to variation of the geomagnetic activity indices and solar wind parameters from the same time interval.
The rest of the paper is structured as follows: in Sect. 2 we describe the processing related to Swarm data and the analysis technique used for monitoring ULF waves with LEO satellites. Section 3 presents our results on Pc3 wave occurrence mapping and the corresponding Pc3 power index for the three Swarm satellites. In Sect. 4 we conclude with a discussion.
LEO observations of ULF waves can only be reliably done and without too much spatial aliasing for the Pc1/Pi1 and Pc2/3 waves. Due to the fast motion through field lines in a LEO orbit, lower-frequency Pc4–5 waves (1–10 MHz) cannot be accurately determined by LEO satellites, their period being longer than the spacecraft transition time through the wave region. Though Pi2 waves have lower frequencies, thanks to their large spatial scales at low latitudes, they have also been detected by LEO satellites (Sutcliffe and Lühr, 2003; Han et al., 2004; Cuturrufo et al., 2015). Two types of Pc3 waves are observed by LEO satellites: intense localized Alfvén-type waves with transverse magnetic disturbance or weak global compression-type waves recorded in the field-aligned component. In this study, we analyze the magnitude of the magnetic field, thus considering the second type of wave.
In particular, we use the low-resolution magnetic field data with a sampling rate of 1 Hz, and hence we had to limit our analysis to the Pc3 class, covering frequencies from 20 MHz (50 s) to 100 MHz (10 s). An electromagnetic wave of higher frequency, e.g., at 200 MHz, would be captured in the low-resolution data by a pulsation with a period of merely 5 data points, making the analysis statistically dubious.
Our method consists of two parts. The first is the construction of a database of daily power spectra, while the second consists of the actual wave detection. For the construction of the database we used the last available version of magnetic data from the vector fluxgate magnetometer (VFM) instrument (version 4.8 for Swarm A and B and versions 4.9 and 4.10 for Swarm C) as well as additional data from the electric field instrument – EFI (version 4). To further enhance our analysis, we also incorporated data from the daily Level 2 products concerning the FAC and IBI (version 2 for both). For details on the definition and derivation of these products, see Park et al. (2013b) and Ritter et al. (2013), respectively.
For every day in the time interval of interest, which spanned the time period from 15 May 2014 to 15 May 2016, we perform the following analysis. First, the magnetic data cdf files corresponding to the day in question are read, along with the files of the previous and next days. Since all spectral methods are plagued by edge effects (Torrence and Compo, 1998), we append the magnetic field time series of the current day, with a few hours long time series from the previous and next days, so that whatever edge effects appear they will affect these additional “margins”, which can then be safely removed from the process, leaving the spectral data of the day under processing free from such issues. From the magnetic time series of the VFM instrument we derive the magnitude of the magnetic field and subtract from it the total field that is predicted, for the same position and moment in time, by the CHAOS-6 model (Finlay et al., 2016). CHAOS-6 is a geomagnetic field model spanning 1999–2016.5, derived from Swarm, CHAMP, Ørsted, and SAC-C satellite magnetic data and ground observatory data. The model uses spatial differences along-track from CHAMP and Swarm and also east–west differences from Swarm (Kotsiaros et al., 2014). To the derived field time series we then apply a Chebyshev type II, zero-phase, high-pass filter with a cutoff frequency of 20 MHz to remove all lower-frequency components from the signal and to place the Pc3 range in the spotlight (Williams and Taylors, 1988).
A series of studies highlighted the significance of applying wavelet analysis, especially its suitability for multi-point, small-scale disturbances, in the investigation of ULF wave events (e.g., Nosé et al., 1998; Balasis et al, 2012; Xu et al., 2013). Using the wavelet method, with the Morlet mother function, we produce the power spectrum of the magnetic field series for 50 logarithmically spaced frequencies from 20 to 100 MHz (Balasis et al., 2013), and remove the aforementioned margins. In parallel to that, the positional vector of the spacecraft is extracted from the files and converted to magnetic coordinates (magnetic latitude, longitude and local time), as well as the electron density series from the EFI data files of the same day. The final spectrum, along with the time series of the magnetic field, the electron density, and all positional information are then exported in a daily file and saved in the database.
The wave detection begins by reading the daily output files and segmenting them in tracks (half-orbits) from −90∘ to +90∘ at magnetic latitude. For each such track, the maximum power per second that is stored in the spectrum is calculated and all segments of consecutive points (seconds) that exceed a threshold of 0.5 nT2 Hz−1 (which roughly corresponds to a pulsation with a minimum amplitude of 0.15 nT) are labeled “candidate events”. Each candidate is tested against a series of criteria that help rule out artificial signals that might result from instrument or telemetry errors. As such, for the candidate event to not be discarded, it must exhibit a duration of at least 2 times its peak period, it must have an amplitude that does not exceed certain limits (10 nT), and it must be smooth enough to constitute a continuous pulsation, so its difference series must always be smaller than ±1 nT. These threshold values have been deduced empirically, by visual examination of a large number of events, and it was found that candidates that exceed these values were polluted by spikes or large discontinuities and thus should be removed from the process. In order to avoid traces of activity from lower Pc classes (below 20 MHz) that have not been completely eradicated by the filtering process, we further demand that the peak of the wave activity be at a frequency that does not lie at the limits of the examined range, so only pulsations with a peak frequency that lies above 21 MHz are accepted.
In order to remove events that are influenced or caused by ESFs at low latitudes, field-aligned or auroral currents at higher latitudes, or in general by other, unclassified anomalies in the electron density profiles, we introduce the Plasma Instabilities category and assign to it all wave-like events that can be attributed to these kinds of phenomena. In order to do so, we impose two criteria on the Level 2 product series and demand that in order for a candidate to be a true Pc3 wave event, it must exhibit a value of bubble probability (as defined in the IBI product) of less than 1 % and a field-aligned current amplitude (taken from the FAC product) that is less than 0.5 µA m−2, both of which must be met for the entire duration of the event. Additionally, if the candidate was detected when the satellite was located in the nightside sector, an additional criterion must be met, namely that its electron density series (extracted from the EFI data files) must not display abrupt changes. In any of these cases the candidate is classified as belonging to the Plasma Instabilities class and is saved in a separate database. On the other hand, if the candidate successfully passes the two criteria for ESF and FAC detection and is located either in the dayside sector or on the nightside, but exhibits a smooth enough electron density series, then it is classified as a Pc3 wave.
In both cases, for every event several characteristics are extracted, such as its duration, peak frequency, average and total power, and bandwidth (the range of frequencies for which the event exhibits power above 50 % of its peak value). All these are saved in a separate matrix for further post-processing and derivation of statistics. For the production of wavemaps, a slightly different approach was used, since waves are by nature extended in space and cannot be accurately represented by a single number (or set of numbers). For this case, the coordinate space, either geographical latitude versus longitude or magnetic latitude versus magnetic local time (MLT), is divided into a 50 by 50 grid, which provides a resolution of 3.6∘ in latitude, 7.2∘ in longitude, and slightly less than half an hour in local time. For every second in the duration of an event, its total Pc3 power is calculated and added to the appropriate grid point to which the measurement belongs, based on the satellite's location at the same moment, thus allowing the entire extent of the wave to be accurately represented. In order to make the resulting maps less dependent on the satellite's orbit, we divide the summed power by the number of seconds the satellite has spent in the corresponding point.
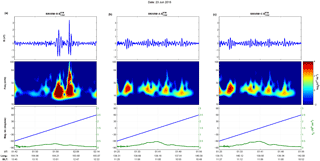
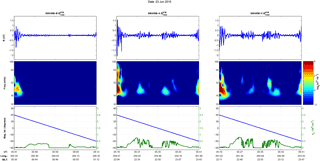
Figure 1Swarm Pc3 wave event. A wave event as detected by the Swarm constellation with Swarm B (a), A (b), and C (c) showing the filtered series of the magnetic field magnitude (top panels), their corresponding wavelet spectra for the joined Pc3 and Pc4 range (middle panels), and a composite plot of the measured electron density (green line) and their location at magnetic latitude (blue line) from −60∘ to +60∘ (bottom panels).
Before delving into the wavemaps and the wave index, it is useful to showcase two examples of the methodology applied for our analysis. In Figs. 1 and 2 we show two tracks that correspond to a dayside (MLT ∼ 11:00) detected wave event and a nightside (MLT ∼ 23:00) episode that is attributed to the presence of an ESF event. The data are taken from 23 June 2015, a day which marked the peak activity in the main phase of a geospace magnetic storm, with a minimum Dst index value of −204 nT, at 05:00 UT. The wave event is captured by the northbound pass of all three satellites, here showing only the part from −60∘ to +60∘ in magnetic latitude, and is depicted from 01:25 to 01:56 UT for the lower Swarm A and C and, a few minutes later, from 01:42 to 02:14 UT for Swarm B. The ESF-related event is detected only by Swarm A and C on their southbound pass from 05:19 to 05:51 UT and is characterized by the two, symmetric around the magnetic Equator, disturbances in the electron density profile. The ESF events or equatorial plasma bubbles are nightside phenomena identified by their plasma signature as sudden depletions in the electron density profile. We also observe in Fig. 2 the corresponding magnetic signature of the specific ESF event (middle panel), which can be easily mistaken, if it is examined alone, for a wave signature unless the accompanying electron density perturbations are taken into account.
Figure 3 shows the magnetic latitude versus MLT map of wave power for all three satellites of the constellation. As can be seen, the bulk of the Pc3 wave activity is located in the equatorial dayside sector (peaking at 09:00, 10:00–11:00, and 12:00–14:00 MLT for Swarm B and at 08:00–09:00, 11:00–12:00, and 14:00–15:00 MLT for A and C), with the two lower satellites A and C displaying statistically greater power than the higher Swarm B. We note that overall the Pc3 wave activity extends to as early as 06:00 and as late as 17:00 MLT. These results are comparable with the ones derived by Balasis et al. (2015b) for 1 year of Swarm data, with the exception of auroral zones (more information on this issue is given later in this section). The small shift of approximately 2 h in the peaks of the activity between Swarm B and the lower pair is attributed to the angular separation of the orbital planes of the satellites, which for the time period examined ranged from 1 to 2 h in local time. This is a strong indication that all satellites, despite their latitudinal and temporal differences, detect the same events (at least as far as the strongest ones are concerned) and just map them in different local times due to the shift in their orbital planes. As this angular separation increases with time, it will further elucidate the extent in local time of Pc3 wave phenomena. The analogous wavemap in geographic coordinates (latitude versus longitude) is shown in Fig. 4. The striking observation here is that most of the activity is located around the area of the South Atlantic Anomaly (SAA), something that has already been mentioned by Balasis et al. (2015b) and is attributed to the lower magnitude of the geomagnetic field in this region, which favors the occurrence of compressional waves.
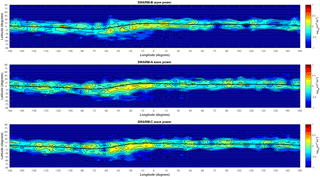
Figure 4Swarm Pc3 wave power map in geographic coordinates. Pc3 wave power per second mapped on the geographic latitude versus geographic longitude grid.
Based on the latitudinal distribution plots of Figs. 3 and 4, there are no Pc3 waves observed at all in the topside ionosphere below −60∘ or above +60∘ in both the magnetic and geographic wave power maps, which is obviously an erroneous result. This outcome arises from the application of the Swarm Level 2 single-spacecraft FAC data product correction in our analysis. Since FAC are practically always present at high latitudes, the inclusion of this Swarm Level 2 product apparently eliminates all the Pc3 wave activity there and interprets it as signatures associated with these currents. For this reason, we have finally decided not to use the Swarm FAC product in deriving the final version of the ULF wave power maps based on 2 years of Swarm data, which are now presented in Figs. 5 and 6 in magnetic and geographic coordinates, respectively.
Summing the total power of each detected wave event for every track (half-orbit) and keeping only daytime tracks, we get the total track-by-track power. To reduce the range of these values, which might differ by several orders of magnitude, we define the Pc3 Power Index as the logarithm (base 10) of the total track-by-track power and hence produce the three Swarm Pc3 Power Indices (one for each satellite), which are shown in the top panels of Figs. 7 and 8. Tracks which exhibit index values below 2 are considered “quiet”, while for the rest we can define three different activity levels: “low” for index values between 2 and 3, “moderate” for values between 3 and 4, and “high” for those with index values above 4.
In an attempt to capture the relation between Pc3 waves and geospace conditions, we incorporate into our analysis the time series of various solar wind parameters and geomagnetic activity indices, downloaded from the OMNIWeb Plus data service of NASA's Space Physics Data Facility. These are the magnitude and three Cartesian components of the interplanetary magnetic field (BIMF) as well as the solar wind velocity (Vsw), both in the GSE coordinate system, the solar wind proton density (Np), temperature (Tp), the solar wind dynamic pressure (Pdyn), Alfvénic speed (VAlfvén), sound speed (Vsound) and, based on the latter, the Mach numbers, both Alfvén (MA) and magnetosonic (MS). In addition to those we derive the magnetic field's cone angle (θB), defined as the angle between the BIMF vector and its component along the Sun–Earth axis (Greenstadt and Olson, 1976), and the magnetopause standoff distance (RMP), defined as (Kivelson and Russell, 1995). Finally, to incorporate the magnetospheric response to the solar wind, we also include two indices of geomagnetic activity, namely the Auroral Electrojet (AE) index and the symmetric disturbance index for the horizontal component of the Earth's magnetic field (SYM-H). The first, being a high-latitude index, operates as an indicator of substorm activity, while the latter is highly correlated with the disturbance storm time (Dst) index and therefore can be regarded as a proxy for the ring current conditions and thus for geomagnetic storms. All these are depicted in the bottom six panels of Figs. 7 and 8 (for clarity we have ignored the vector components of BIMF and Vsw and show only their magnitude).

Figure 5Swarm Pc3 wave power map in magnetic coordinates without the FAC correction. As in Fig. 3 without the application of the Swarm Level 2 single-spacecraft FAC data product.
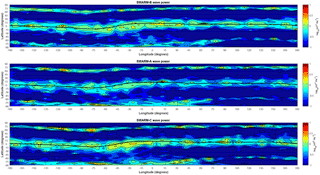
Figure 6Swarm Pc3 wave power map in geographic coordinates without the FAC correction. As in Fig. 4 without the application of the Swarm Level 2 single-spacecraft FAC data product.
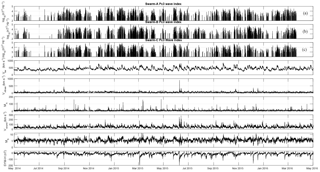
Figure 7Swarm ULF wave index time series. From top to bottom: Pc3 power indices for the three satellites of the Swarm constellation (A: first panel, B: second panel, C: third panel), solar wind parameters (Vsw, VAlfvén, MA, Vsound, MS) and the SYM-H index. Ticks on the x axis denote the middle of the corresponding month.
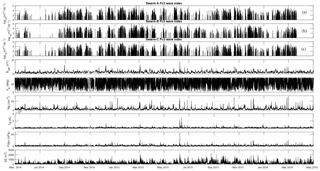
Figure 8Swarm ULF wave index time series. From top to bottom: Pc3 power indices for the three satellites of the Swarm constellation (A: first panel, B: second panel, C: third panel), solar wind parameters (BIMF, θB, Np, Tp, Pdyn), and the AE index. Ticks on the x axis denote the middle of the corresponding month.
To calculate the correlations between the three Swarm Pc3 Indices and the various solar wind parameters and geomagnetic indices, we considered all possible pairwise combinations, interpolated the parameter series to the timestamps of each Pc3 Index (using a simple, linear interpolation scheme), and computed the Pearson correlation coefficient (Pearson, 1895). The results of this analysis, for all possible combinations, can be seen in Table 1. Looking at the table it becomes evident that the parameter that is most correlated with Pc3 wave activity is the solar wind velocity and especially its component along the XGSE axis. The negative sign in the VxGSE correlation just points out the obvious fact that it is the earthward direction that is related to the generation of Pc3 waves. This observation is well known in the literature, as was first made in the 60s (Saito, 1964), but its presence can be seen as a validation of our methodology. Next in order of importance are the magnetosonic Mach number MS and its corresponding velocity Vsound, along with the magnetopause standoff distance RMP. For the latter the negative sign indicates that enhanced Pc3 activity takes place when the magnetosphere is most compressed by the solar wind and thus when RMP exhibits lower values. All these reinforce the idea of Pc3 waves being generated at the bow shock and propagating as compressional mode waves up until the ionosphere, where they are detected by the Swarm satellites (Yumoto et al., 1984; Heilig et al., 2007). Conversely, on the ground these waves are detected as surface geomagnetic pulsations, and thus there the prominent factors are the Alfvénic velocity and its respective Alfvénic Mach number (Heilig et al., 2010), instead of the magnetosonic one which applies to our case. Finally, the last two important parameters are the cone angle, which seems to indicate that enhancements in Pc3 activity are related to low θB values and thus to more horizontal BIMF configurations, and the solar wind's proton temperature Tp. In general though, all correlation values are very low, a fact that is due to the large noise component that characterizes all time series, since for most of the time examined the solar wind parameters exhibit very low (background) levels of activity which are only sparsely interrupted by intense events. We have repeated the analysis using a moving time window with a length that corresponds to 50 tracks, in which case we noticed that for some geomagnetically disturbed periods, the values of the correlations for various parameters can increase dramatically. As an example, for the Pc3 activity at the tail of the August 2014 storm we get correlations with the Vsw that achieve values as high as 0.64 and, for the MS, values as high as 0.47. Unfortunately, the increase in the correlations does not always follow the increase in geomagnetic activity, so the interplay between these parameters is much more complex and almost certainly governed by nonlinear interactions, although their order of importance remains roughly the same.
As an extra step, we shifted the various parameters' time series by as much as 48 h before and after their actual timestamps, with a time step of 1 h, and re-calculated the correlations, to see whether some specific time lag might yield better results, since the conditions in the solar wind might need several minutes up to a few hours to drive Pc3 waves and allow them to penetrate into the inner magnetosphere until their effects are detected by the Swarm satellites in LEO. Unfortunately this did not yield any meaningful results, since most of the above-mentioned quantities exhibit their peak correlation values for zero time lag and, when they do not, they do not seem to do so in a consistent way for all three satellite indices. The only possible exception is the velocities Vsw and Vsound, which show marginally better correlation factors for a time lag of 2 to 6 h, but the improvements are so small that it is difficult to draw any conclusions from that fact alone.
Table 1Correlation coefficients for each pairwise combination between the three Swarm Pc3 indices and each of the solar wind or geospace parameters for the entire May 2014 to May 2016 period.
As for the magnetospheric response to the solar wind, it can be said that the relation between Pc3 waves and magnetic storms is not a simple one. Great storms always coincide with enhancements in Pc3 activity, as can be seen for the January, March, June, October, and December events of 2015, while the extremely quiet period of July and August 2014 also appears completely silent in the wave power series. On the other hand though, significant increases in Pc3 activity do not always coincide with geomagnetic disturbances, as can be seen in the distinct example of February 2015, although for that period there was a moderate increase in Vsw and Np that consequently led to an increase in MS. From the two indices employed here, the SYM-H seems to be more correlated with the type of activity that is captured by our Pc3 index, as we mostly focus on equatorial to mid-latitudinal wave activity. The level of the correlations though is again quite low, contrary to the widely spread misbelief that ULF power and geomagnetic activity are closely correlated. This misbelief was refuted recently by Currie and Waters (2014) and it is also evident here, as well.
Our findings on Pc3 wave power distribution in magnetic and geographic coordinates based on 24 months of Swarm VFM observations (Figs. 5–6) confirm the results of a previous study on Pc3 wave power features in the topside ionosphere revealed by 1 year of Swarm absolute scalar magnetometer (ASM) observations (Balasis et al., 2015b). It is worth mentioning that the present study uses a different methodology for the selection of wave events involving additional steps and following the detection of candidate events with a wavelet analysis technique and the requirement of a smooth profile for the electron density data of the previous study. Here, we incorporate additional analysis steps consisting of the application of the CHAOS-6 model (prior to the wavelet analysis) and the utilization of Swarm Level 2 products (i.e., the FAC and IBI products) to impose constraints on the Swarm data for the wave event selection.
Forsyth et al. (2017) suggested that many of the magnetic field perturbations on small scales may contain a significant fraction of perturbations which are the result of wave activity in the vicinity of the spacecraft or current sheets inclined to the motion of the spacecraft. As a result, they noted that extreme care must be taken in interpreting the temporal variation of the magnetic field observed by a moving spacecraft as relating to the spatial structures which can be used to infer field-aligned currents. Moreover, they suggested that since such assumptions are used to produce the Swarm Level 2 single-spacecraft FAC data product (Ritter et al., 2013), care should be taken when using or interpreting this data product as well. Our results also demonstrate that the inclusion of this product to constrain the wave activity in Swarm wave power maps inevitably eliminates all the wave activity at high latitudes, which is physically unrealistic (Figs. 3 and 4). Therefore, we have dropped the use of the Swarm FAC product in deriving the final version of ULF wave power maps based on Swarm observations from May 2014 to May 2016. However, we cannot rule out the possibility that a fraction of the high-latitude wave activity seen in these maps (Figs. 5 and 6) is probably attributed to the distribution of field-aligned currents.
In this study, we demonstrate how a Swarm daytime, track-by-track Pc3 wave index can be systematically derived for the topside ionosphere calculated using 2 years of the constellation's data. This is the first attempt, at least to our knowledge, to derive a ULF wave index from LEO satellite data (see, e.g., Borovsky and Denton, 2014). Consequently, we compare the variations of Swarm wave index values to corresponding variations of solar wind variables and geomagnetic activity indices in order to search for possible correlations between them. Indeed, for epochs around intense magnetic storms (cf. the storm events of March, June, and December 2015), there seems to be an increase in Pc3 activity and the values of the Pc3 indices were shown to correlate with parameters that are well known as suspects for driving of Pc3 waves, like Vsw, Vsound, RMP, and θB. In the future we plan to examine the possibility of extending the formulation of the index in a manner similar to the one introduced by Russell and Fleming (1976), by including the average frequency of the wave events that have been aggregated for each track and that possibly also incorporate the values of some index of geomagnetic activity (e.g., Kp). Moreover, the same technique can also be applied to derive a higher-frequency Swarm ULF wave index (e.g., in the Pc1 band) using the high-resolution (i.e., 50 Hz) VFM data from the mission. Pc1 waves are a critical element of space weather as they are considered responsible for the energetic-particle pitch-angle diffusion in radiation belts.
Motivated by the potential importance of enhanced ULF wave activity for particle energization in radiation belts and hence space weather effects, Kozyreva et al. (2007) and Romanova and Pilipenko (2009) proposed the calculation of the ULF wave index in the Pc5 band from ground-based magnetometer data, and, more recently, Pilipenko et al. (2017) outlined possible directions of this index advancement. Waters and Menk (2016) suggested that a ground Pc3 pulsation index may be useful for identifying contamination by background activity in geomagnetic and aeromagnetic surveys used in geophysical exploration. Based on the results by Heilig et al. (2010) from ground magnetometers, further development of Pc3 activity indices as proxies of solar wind conditions was also recommended (Waters and Menk, 2016). Therefore, the Swarm ULF wave index proposed here can be considered a candidate for a standard Level 2 mission product aiming at the potential identification of episodes with persistent enhanced solar wind activity. An alternative option could be to launch a website that provides a database with a provisional Pc3 index, which would be made available to the international community for testing and validation. Ultimately, the new index can potentially serve as an integral part of a space weather risk assessment scheme for the critical infrastructure existing in the near-Earth electromagnetic environment.
All data are available through the ESA Earth Online platform, after registration for an ESA Earth Observation Users' Single Sign On account https://earth.esa.int/web/guest/umsso?orig_request=/web/guest/picommunity/myearthnet (ESA, 2018). The AE and SYM-H indices data have been obtained from the World Data Center for Geomagnetism of Kyoto University at http://wdc.kugi.kyoto-u.ac.jp/index.html (WDC, 2018), whereas the solar wind data have been retrieved through the NASA OMNIWeb space physics data facility at http://omniweb.gsfc.nasa.gov/ (GSFC, 2018).
The authors declare that they have no conflict of interest.
This article is part of the special issue “Dynamics and interaction of processes in the Earth and its space environment: the perspective from low Earth orbiting satellites and beyond”. It is not associated with a conference.
This study makes use of data from the Swarm spacecraft mission, which is
funded and managed by the European Space Agency. We acknowledge support of
this work by the PROTEAS II project (MIS 5002515), which is implemented under
the “Reinforcement of the Research and Innovation Infrastructure” action,
funded by the ”Competitiveness, Entrepreneurship and Innovation” operational
programme (NSRF 2014-2020) and co-financed by Greece and the European Union
(European Regional Development Fund).
The topical editor, Rumi Nakamura, thanks Vyacheslav Pilipenko and two
anonymous referees for help in evaluating this paper.
Alken, P., Maus, S., Chulliat, A., Vigneron, P., Sirol, O., and Hulot G.: Swarm equatorial electric field chain: First results, Geophys. Res. Lett., 42, 673–680, https://doi.org/10.1002/2014GL062658, 2015.
Archer, W. E., Knudsen, D. J., Burchill, J. K., Patrick, M. R., and St.-Maurice, J. P.: Anisotropic core ion temperatures associated with strong zonal flows and upflows, Geophys. Res. Lett., 42, 981–986, https://doi.org/10.1002/2014GL062695, 2015.
Balasis, G., Daglis, I. A., Zesta, E., Papadimitriou, C., Georgiou, M., Haagmans, R., and Tsinganos, K.: ULF wave activity during the 2003 Halloween superstorm: multipoint observations from CHAMP, Cluster and Geotail missions, Ann. Geophys., 30, 1751–1768, https://doi.org/10.5194/angeo-30-1751-2012, 2012.
Balasis, G., Daglis, I. A., Georgiou, M., Papadimitriou, C., and Haagmans, R.: Magnetospheric ULF wave studies in the frame of Swarm mission: A time-frequency analysis tool for automated detection of pulsations in magnetic and electric field observations, Earth Planets Space, 65, 1385–1398, 2013.
Balasis, G., Daglis, I. A., Mann, I. R., Papadimitriou, C., Zesta, E., Georgiou, M., Haagmans, R., and Tsinganos, K.: Multi-satellite study of the excitation of Pc3 and Pc4-5 ULF waves and their penetration across the plasmapause during the 2003 Halloween superstorm, Ann. Geophys., 33, 1237–1252, https://doi.org/10.5194/angeo-33-1237-2015, 2015a.
Balasis, G., Papadimitriou, C., Daglis, I. A., and Pilipenko, V.: ULF wave power features in the topside ionosphere revealed by Swarm observations, Geophys. Res. Lett., 42, 6922–6930, https://doi.org/10.1002/2015GL065424, 2015b.
Borovsky, J. E. and Denton, M. H.: Exploring the cross correlations and autocorrelations of the ULF indices and incorporating the ULF indices into the systems science of the solar wind-driven magnetosphere, J. Geophys. Res.-Space, 119, 4307–4334, https://doi.org/10.1002/2014JA019876, 2014.
Buchert, S., Zangerl, F., Sust, M., Andre, M., Eriksson, A., Wahlund, J., and Opgenoorth, H.: SWARM observations of equatorial electron densities and topside GPS track losses, Geophys. Res. Lett., 42, 2088–2092, https://doi.org/10.1002/2015GL063121, 2015.
Chi, P. J. and Le, G.: Observations of magnetospheric high-m poloidal waves by ST-5 satellites in low Earth orbit during geomagnetically quiet times, J. Geophys. Res., 120, 4776–4783, https://doi.org/10.1002/2015JA021145, 2015.
Civet, F., Thebault, E., Verhoeven, O., Langlais, B., and Saturnino, D.: Electrical conductivity of the Earth's mantle from the first Swarm magnetic field measurements, Geophys. Res. Lett., 42, 3338–3346, https://doi.org/10.1002/2015GL063397, 2015.
Currie, J. L. and Waters, C. L.: On the use of geomagnetic indices and ULF waves for earthquake precursor signatures, J. Geophys. Res., 119, 992–1003, https://doi.org/10.1002/2013JA019530, 2014.
Cuturrufo, F., Pilipenko, V., Heilig, B., Stepanova, M., Lühr, H., Vega, P., and Yoshikawa, A.: Near-equatorial Pi2 and Pc3 waves observed by CHAMP and on SAMBA/MAGDAS stations, Adv. Space Res. 55, 1180–1189, 2015.
De Michelis, P., Consolini, G., and Tozzi, R.: Magnetic field fluctuation features at Swarm's altitude: A fractal approach, J. Geophys. Res., 42, 3100–3105, https://doi.org/10.1002/2015GL063603, 2015.
Dunlop, M. W., Yang, J.-Y., Yang, Y.-Y., Xiong, C., Lühr, H., Bogdanova, Y. V., Shen, C., Olsen, N., Zhang, Q.-H., Cao, J.-B., Fu, H.-S., Liu, W.-L., Carr, C. M., Ritter, P., Masson, A., and Haagmans, R.: Simultaneous field-aligned currents at Swarm and Cluster satellites, Geophys. Res. Lett., 42, 3683–3691, https://doi.org/10.1002/2015GL063738, 2015.
Engebretson, M. J., Posch, J. L., Westerman, A. M., Otto, N. J., Slavin, J. A., Le, G., Strangeway, R. J., and Lessard, M. R.: Temporal and spatial characteristics of Pc1 waves observed by ST5, J. Geophys. Res. 113, A07206, https://doi.org/10.1029/2008JA013145, 2008.
ESA: ESA Earth Observation User Data, available at: https://earth.esa.int/web/guest/umsso?orig_request=/web/guest/picommunity/myearthnet, last access: 5 March 2018.
Finlay, C. C., Olsen, N., Kotsiaros, S., Gillet, N., and Toeffner-Clausen, L.: Recent geomagnetic secular variation from Swarm and ground observatories as estimated in the CHAOS-6 geomagnetic field model, Earth Planets Space, 68, 1–18, https://doi.org/10.1186/s40623-016-0486-1, 2016.
Friis-Christensen, E., Lühr, H., and Hulot, G.: Swarm: A constellation to study the Earth's magnetic field, Earth Planets Space, 58, 351–358, 2006.
Forsyth, C., Rae, I. J., Mann, I. R., and Pakhotin, I. P.: Identifying intervals of temporally invariant field-aligned currents from Swarm: Assessing the validity of single-spacecraft methods, J. Geophys. Res., 122, 3411–3419, https://doi.org/10.1002/2016JA023708, 2017.
Goodwin, L. V., Iserhienrhien, B., Miles, D. M., Patra, S., van der Meeren, C., Buchert, S. C., Burchill, J. K., Clausen, L. B. N., Knudsen, D. J., McWilliams, K. A., and Moen, J.: Swarm in situ observations of F region polar cap patches created by cusp precipitation, Geophys. Res. Lett., 42, 996–1003, https://doi.org/10.1002/2014GL062610, 2015.
Greenstadt, E. W. and Olson, J. V.: Pc 3,4 Activity and Interplanetary Field Orientation, J. Geophys. Res., 81, 5911–5920, 1976.
GSFC: Solar wind data, available at: http://omniweb.gsfc.nasa.gov/, last access: 5 March 2018.
Han, D.-S., Iyemori, T., Nose, M., McCreadie, H., Gao, Y., Yang, F., Yamashita, S., and Stauning, P.: A comparative analysis of low-latitude Pi2 pulsations observed by Ørsted and ground stations, J. Geophys. Res., 109, A10209, https://doi.org/10.1029/2004JA010576, 2004.
Heilig, B. and Sutcliffe, P. R.: Coherence and phase structure of compressional ULF waves at low-Earth orbit observed by the Swarm satellites, Geophys. Res. Lett., 43, 945–951, https://doi.org/10.1002/2015GL067199, 2016.
Heilig, B., Lühr, H., and Rother, M.: Comprehensive study of ULF upstream waves observed in the topside ionosphere by CHAMP and on the ground, Ann. Geophys., 25, 737–754, https://doi.org/10.5194/angeo-25-737-2007, 2007.
Heilig, B., Lotz, S., Vero, J., Sutcliffe, P., Reda, J., Pajunpää, K., and Raita, T.: Empirically modelled Pc3 activity based on solar wind parameters, Ann. Geophys., 28, 1703–1722, https://doi.org/10.5194/angeo-28-1703-2010, 2010.
Heilig, B., Sutcliffe, P. R., Ndiitwani, D. C., and Collier, A. B.: Statistical study of geomagnetic field line resonances observed by CHAMP and on the ground, J. Geophys. Res., 118, 1934–1947, https://doi.org/10.1002/jgra.50215, 2013.
Hulot, G., Vigneron, P., Léger, J.-M., Fratter, I., Olsen, N., Jager, T., Bertrand, F., Brocco, L., Sirol, O., Lalanne, X., Boness, A., and Cattin, V.: Swarm's absolute magnetometer experimental vector mode, an innovative capability for space magnetometry, Geophys. Res. Lett., 42, 1352–1359, https://doi.org/10.1002/2014GL062700, 2015.
Iyemori, T. and Hayashi, K.: Pc 1 micropulsations observed by Magsat in the ionospheric F region, J. Geophys. Res., 94, 93–100, 1989.
Iyemori, T., Nakanishi, K., Aoyama, T., Yokoyama, Y., Koyama, Y., and Lühr, H.: Confirmation of existence of the small-scale field-aligned currents in middle and low latitudes and an estimate of time scale of their temporal variation, Geophys. Res. Lett., 42, 22–28, https://doi.org/10.1002/2014GL062555, 2015.
Jadhav, G., Rajaram, M., and Rajaram, R.: Modification of daytime compressional waves by the ionosphere: First results from OERSTED, Geophys. Res. Lett., 28, 103–106, 2001.
Kivelson, M. G. and Russell, C. T.: Introduction to space physics, Cambridge University Press, London, UK, 1995.
Kotsiaros S., Finlay, C. C., and Olsen, N.: Use of along-track magnetic field differences in lithospheric field modelling, Geophys. J. Int., 200, 878–887, 2014.
Kozyreva, O., Pilipenko, V., Engebretson, M. J., Yumoto, K., Watermann, J., and Romanova, N.: In search of a new ULF wave index: Comparison of Pc5 power with dynamics of geostationary relativistic electrons, Planet. Space Sci., 55, 755–769, https://doi.org/10.1016/j.pss.2006.03.013, 2007.
Le, G., Chi, P. J., Strangeway, R. J., and Slavin, J. A.: Observations of a unique type of ULF wave by low-altitude Space Technology 5 satellites, J. Geophys. Res., 116, A08203, https://doi.org/10.1029/2011JA016574, 2011.
Lühr, H., Park, J., Gjerloev, J. W., Rauberg, J., Michaelis, I., Merayo, J. M. G., and Brauer, P.: Field-aligned currents' scale analysis performed with the Swarm constellation, Geophys. Res. Lett., 42, 1–8, https://doi.org/10.1002/2014GL062453, 2015a.
Lühr, H., Kervalishvili, G., Michaelis, I., Rauberg, J., Ritter, P., Park, J., Merayo, J. M. G., and Brauer, P.: The interhemispheric and F region dynamo currents revisited with the Swarm constellation, Geophys. Res. Lett., 42, 3069–3075, https://doi.org/10.1002/2015GL063662, 2015b.
Ndiitwani, D. C. and Sutcliffe, P. R.: The structure of low-latitude Pc3 pulsations observed by CHAMP and on the ground, Ann. Geophys., 27, 1267–1277, https://doi.org/10.5194/angeo-27-1267-2009, 2009.
Nosé, M., Iyemori, T., Takeda, M., Kamei, T., Milling, D. K., Orr, D., Singer, H. J., Worthington, E. W., and Sumitomo, N.: Automated detection of Pi 2 pulsations using wavelet analysis: 1. Method and an application for substorm monitoring, Earth Planets Space, 50, 773–783, 1998.
Olsen, N., Hulot, G., Lesur, V., Finlay, C. C., Beggan, C., Chulliat, A., Sabaka, T. J., Floberghagen, R., Friis-Christensen, E., Haagmans, R., Kotsiaros, S., Lühr, H., Töffner-Clausen, L., and Vigneron, P.: The Swarm Initial Field Model for the 2014 geomagnetic field, Geophys. Res. Lett., 42, 1092–1098, https://doi.org/10.1002/2014GL062659, 2015.
Olsen, N., Stolle, C., Floberghagen, R., Hulot, G., and Kuvshinov, A.: Special issue “Swarm science results after 2 years in space”, Earth Planets Space, 68, 1–3, https://doi.org/10.1186/s40623-016-0546-6, 2016.
Park, J., Lühr, H., and Rauberg, J.: Global characteristics of Pc1 magnetic pulsations during solar cycle 23 deduced from CHAMP data, Ann. Geophys., 31, 1507–1520, https://doi.org/10.5194/angeo-31-1507-2013, 2013a.
Park, J., Noja, M., Stolle, C., and Lühr, H.: The Ionospheric Bubble Index deduced from magnetic field and plasma observations onboard Swarm, Earth Planets Space, 65, 1333–1344, 2013b.
Park, J., Stolle, C., Xiong, C., Lühr, H., Pfaff, R. F., Buchert, S., and Martinis, C. R.: A dayside plasma depletion observed at midlatitudes during quiet geomagnetic conditions, Geophys. Res. Lett., 42, 967–974, https://doi.org/10.1002/2014GL062655, 2015.
Pearson, K.: Notes on regression and inheritance in the case of two parents, P. R. Soc. London, 58, 240–242, 1895.
Pilipenko, V. A., Kozyreva, O. V., Engebretson, M. J., and Soloviev, A. A.: ULF wave power index for space weather and geophysical applications: A review, Russ. J. Earth Sci., 17, ES1004, https://doi.org/10.2205/2017ES000597, 2017.
Pitout, F., Marchaudon, A., Blelly, P.-L., Bai, X., Forme, F., Buchert, S. C., and Lorentzen, D. A.: Swarm and ESR observations of the ionospheric response to a field-aligned current system in the high-latitude midnight sector, Geophys. Res. Lett., 42, 4270–4279, https://doi.org/10.1002/2015GL064231, 2015.
Ritter, P., Lühr, H., and Rauberg, J.: Determining field-aligned currents with the Swarm constellation mission, Earth Planets Space, 65, 1285–1294, 2013.
Romanova, N. and Pilipenko, V.: ULF wave indices to characterize the solar wind-magnetosphere interaction and relativistic electron dynamics, Acta Geophys., 57, 158–170, https://doi.org/10.2478/s11600-008-0064-4, 2009.
Russell, C. T. and Fleming, B. K.: Magnetic pulsations as a probe of the interplanetary magnetic field: A test of the Borok B Index, J. Geophys. Res., 81, 5882–5886, https://doi.org/10.1029/JA081i034p05882, 1976.
Saito, T.: A new index of geomagnetic pulsation and its relation to solar M-regions, Rep., Ionos. Space Res., Japan, 18, 260–274, 1964.
Schnepf, N. R., Kuvshinov, A., and Sabaka, T.: Can we probe the conductivity of the lithosphere and upper mantle using satellite tidal magnetic signals?, Geophys. Res. Lett., 42, 3233–3239, https://doi.org/10.1002/2015GL063540, 2015.
Spicher, A., Cameron, T., Grono, E. M., Yakymenko, K. N., Buchert, S. C., Clausen, L. B. N., Knudsen, D. J., McWilliams, K. A., and Moen, J. I.: Observation of polar cap patches and calculation of gradient drift instability growth times: A Swarm case study, Geophys. Res. Lett., 42, 201–206, https://doi.org/10.1002/2014GL062590, 2015.
Sutcliffe, P. R. and Lühr, H.: A comparison of Pi2 pulsations observed by CHAMP in low Earth orbit and on the ground at low latitudes, Geophys. Res. Lett., 30, 2105, https://doi.org/10.1029/2003GL018270, 21, 2003.
Stolle, C., Lühr, H., Rother, M., and Balasis, G.: Magnetic signatures of equatorial spread F as observed by the CHAMP satellite, J. Geophys. Res., 111, A02304, https://doi.org/10.1029/2005JA011184, 2006.
Torrence, C. and Compo, G. P.: A practical guide to wavelet analysis, B. Am. Meteorol. Soc., 79, 1, 61–78, 1998.
Vellante, M., Lühr, H., Zhang, T. L., Wesztergom, V., Villante, U., De Lauretis, M., Piancatelli, A., Rother, M., Schwingenschuh, K., Koren, W., and Magnes, W.: Ground/satellite signatures of field line resonance: A test of theoretical predictions, J. Geophys. Res., 109, A06210, https://doi.org/10.1029/2004JA010392, 2004.
Waters, C. and Menk, F.: Monitoring Magnetospheric Waves from the Ground, Waves, Particles, and Storms in Geospace, edited by: Balasis, G., Daglis, I. A., and Mann, I. R., Oxford University Press, Oxford, UK, 2016.
WDC: AE and SYM-H indices data, available at: http://wdc.kugi.kyoto-u.ac.jp/index.html, last access: 5 March 2018.
Williams, A. B. and Taylors, F. J.: Electronic Filter Design Handbook, McGraw-Hill, New York, USA, ISBN 0-07-070434-1, 1988.
Xu, Z., Gannon, J. L., and Rigler, E. J.: Report of geomagnetic pulsation indices for space weather applications, US Geological Survey Open-File Report 2013–1166, 22 pp., availabe at: http://pubs.usgs.gov/of/2013/1166/ (last access: 18 January 2018), 2013.
Yagova, N., Heilig, B., and Fedorov, E.: Pc2-3 geomagnetic pulsations on the ground, in the ionosphere, and in the magnetosphere: MM100, CHAMP, and THEMIS observations, Ann. Geophys., 33, 117–128, https://doi.org/10.5194/angeo-33-117-2015, 2015.
Yumoto, K., Saito, T., Tsurutani, B. T., Smith, E. J., and Akasofu, S.-I.: Relationship between the IMF magnitude and Pc 3 magnetic pulsations in the magnetosphere, J. Geophys. Res., 89, 9731–9740, 1984.
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
- Article
(4171 KB) - Full-text XML