the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
On the approximation of spatial structures of global tidal magnetic field models
Roger Telschow
Christian Gerhards
Martin Rother
The extraction of the magnetic signal induced by the oceanic M2 tide is typically based solely on the temporal periodicity of the signal. Here, we propose a system of tailored trial functions that additionally takes the spatial constraint into account that the sources of the signal are localized within the oceans. This construction requires knowledge of the underlying conductivity model but not of the inducing tidal current velocity. Approximations of existing tidal magnetic field models with these trial functions and comparisons with approximations based on other localized and nonlocalized trial functions are illustrated.
Conductive seawater moving through the ambient Earth's main magnetic field Bmain induces a secondary magnetic field Boc. Due to their periodic nature, magnetic signals generated by ocean tides are particularly easy to detect and have been studied in observatory data as early as, e.g., Malin (1970). However, the extraction of global models for magnetic fields induced by the dominating M2 tide from satellite data has only recently become possible (e.g., Sabaka et al., 2015, 2016; Tyler et al., 2003). Although the extraction procedures used are solely based on the temporal periodicity of the tidal signal (and not on further information on the spatial localization of the sources), they seem, by visual inspection, to coincide very well with results obtained by forward models such as in Kuvshinov and Olsen (2005). A more extensive comparison of forward models of electromagnetic ocean tidal signals based on different ocean tide models has recently been published in Saynisch et al. (2018). In that work, it was shown that the residuals between the different models can exceed the nominal noise level of the Swarm satellite mission. The ability to extract M2 tidal magnetic field signals in satellite data more precisely can therefore help in constraining ocean tide models. In Grayver et al. (2016) and Schnepf et al. (2015) it has been shown that an M2 tidal magnetic field model can also be used to constrain 1-D models of the Earth's mantle conductivity, and forward studies in Irrgang et al. (2016) have shown that lateral variations in the conductivity of the ocean water itself should have a detectable influence on the measured magnetic field (although the latter study was performed for general ocean circulation and not for tidal current systems).
In this short paper, we want to illustrate the effects that different (spatially localized) sets of trial functions can have on the approximation of the magnetic field induced by the M2 tide in the first place.
In particular, we describe a possible setup for the inclusion of spatial localization constraints (in addition to the constraint of temporal periodicity) for the approximation of ocean-tide-induced magnetic fields. Clearly, the velocity field u that is responsible for the generation of the corresponding secondary magnetic field Boc vanishes over the continents. The precise connection between u and Boc is given by the time-harmonic Maxwell equations:
where we assume to have knowledge of Bmain, the underlying conductivity σ, and the frequency ω. Furthermore, E denotes the electric field and μ0 is the vacuum permeability. Instead of using a fixed velocity field u, we substitute it by a set of functions (e.g., vectorial Slepian functions as in Plattner and Simons (2014, 2015) that are localized over the oceans) to obtain a set of corresponding trial functions that each solve Eq. (1). The latter is suitable for the approximation of Boc and reflects the spatial localization of the sources of the induced magnetic signal in the oceans. Thus, a magnetic field model that is based on an expansion of the signal in terms of the function system automatically reflects the spatial origin of the signal as well as its temporal periodicity (described by the frequency ω). Additionally, due to the linear connection between u and Boc, an approximation of Boc directly yields an approximation of the underlying tidal current velocity u in terms of the functions . However, a model of the underlying conductivity σ has to be assumed for the construction of the Bℓ. Throughout this paper, we fix the underlying conductivity, meaning that we do not test the influence of a variation of the conductivity model on the approximation of Boc. The goal of the paper is rather the illustration of the effect of the general constraint that the (unknown) underlying u is restricted to the oceans. In a forthcoming study, the simultaneous reconstruction of u and approximation of Boc, and a comparison with existing models, shall be investigated more thoroughly. Since the connection between σ and Boc is nonlinear, a simultaneous determination of σ and Boc (assuming a fixed velocity field model for u) is not as straightforward. A detailed description of the trial functions is provided in Sect. 2.
In Sect. 3, we illustrate our approach with input data derived from the (satellite- and observatory-data-based) CM5 model of Sabaka et al. (2015) and from data derived from a forward model based on the X3DG solver from Kuvshinov (2008). We approximate these input data sets separately in terms of time-periodic vector spherical harmonics, a system of spatially localized trial functions that contains no particular information on the underlying sources (in our case, Abel–Poisson kernels), and the new set of trial functions indicated in the previous paragraph, respectively. We also include an example with artificial continental noise. The residuals with respect to the input data show that the use of the function system can filter out undesired contributions to the M2 tidal magnetic field over the continents, without neglecting data over the continents. These residuals can reach up to 15% of the maximal signal strength and have a magnitude that should be detectable at satellite altitude.
Given a so-called dictionary 𝒟 of trial functions, we use the Regularized (Orthogonal) Functional Matching Pursuit (cf. Fischer and Michel, 2013; Michel and Telschow, 2014, 2016 for details) for the approximation of Boc. Briefly speaking, this is a greedy-type algorithm that yields an approximation
of Boc by iteratively choosing coefficients αi∈ℝ and dictionary elements di∈𝒟 via
denotes the residual between the data b∈ℝM and the approximation after i−1 iterations. In this particular setup, ℱ represents the linear operator that evaluates a function at the M locations where data are provided, and ℋ is a suitable Hilbert space for the regularization of the problem1. The parameter λ controls the trade-off between the data misfit and the regularizing term , which imposes a certain property to such as smoothness (as in our case). The Regularized (Orthogonal) Functional Matching Pursuit, in general, has the advantage that it can easily deal with different dictionaries 𝒟 (or combinations of such) from which the approximant is built. However, any other approximation method could be used as well with the proposed function systems. In this paper, we use the term “dictionary” simply to describe a set of arbitrary functions that we consider suitable for our purposes. These functions do not necessarily have to satisfy particular mathematical properties such as orthogonality or completeness. Therefore, we call such functions “trial functions” rather than, e.g., “basis functions”.
In the following, we briefly introduce some function systems that can be used for the constitution of 𝒟. In particular, Sect. 2.4 describes in more detail the aforementioned trial functions that contain temporal and spatial constraints tailored for ocean-tide-induced magnetic fields.
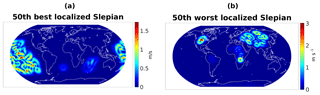
Figure 2Absolute value of the vectorial Slepian function with 50th best localization over the oceans (a) and with the 50th worst localization over the oceans (b), for bandlimit N=40.
2.1 Vector spherical harmonics
We briefly recapitulate the notion of classical vector spherical harmonics in a form that we need at a few occasions later on. By , we denote the sphere of radius r, while 𝕊=𝕊1 stands for the unit sphere. Every unit vector can be expressed in spherical coordinates with longitude φ and polar distance t=cos(ϑ), where ϑ is the corresponding co-latitude. By Yn,k, we denote fully normalized spherical harmonics of degree n and order k: for every n∈ℕ0 and ,
The involved associated Legendre functions are, for , defined as
If f is a scalar-valued square-integrable function on 𝕊, then, for every degree n∈ℕ0 and order , the values
are called the Fourier coefficients of the function f.
Going over to the vectorial setting, it is well known that every square-integrable vector field f on the unit sphere can be uniquely decomposed into its radial and two tangential components such that
with scalar-valued functions and the radial unit vector . By the surface gradient ∇𝕊, we denote the tangential component of the usual Euclidean gradient ∇, i.e.,
with unit vectors and . Moreover, the surface curl gradient L𝕊 is defined by , where × is the usual cross product in ℝ3. In other words,
Hence, we define three types of vector spherical harmonics: the radial
for degrees n≥0 and orders , as well as the tangential
for degrees n≥1 and orders . Note that, for convenience, we set . It should further be noted that the vector spherical harmonics in Eq. (4) are surface-curl-free while those in Eq. (5) are surface-divergence-free. In analogy to Eq. (3), we can now define the Fourier coefficients
of square-integrable vector fields f on the unit sphere.
The vector spherical harmonics from above are defined solely on the unit sphere and can, therefore, only be used for the expansion of vector-valued functions on 𝕊. However, for the approximation of satellite potential field data it is necessary to have related functions that are also defined in the exterior of a sphere. For that purpose, we define the following gradients of harmonic extensions of (scalar) spherical harmonics:
for and , where a is the radius of a reference sphere, e.g., Earth's mean radius.
2.2 Vectorial Abel–Poisson kernel
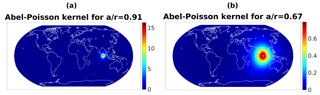
While the set of functions from Eq. (6) is suitable for the global approximation of potential field data, we are also interested in localized functions. One possible choice is the Abel–Poisson kernel (see, e.g., Freeden and Gerhards, 2012; Freeden et al., 1998). For , , it is defined by
That is, with unit vectors and radii , we have
which shows that K only depends on the spherical distance between ξ and η, since . Therefore, the kernel is radially symmetric if we keep one of the variables fixed (we strictly keep the second argument fixed, here aη). The degree of localization is determined by the ratio . The closer it is to 1, i.e., the smaller the difference between the radii a and r, the better the spatial localization of around η. In our case, we choose a to be the Earth's mean radius, and r is the radius of the sphere at which we evaluate the kernel. An illustration of the kernel is provided in Fig. 1.
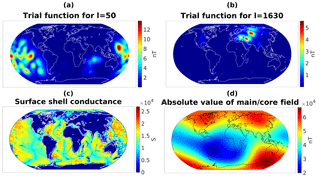
Figure 3Absolute value of the trial function corresponding to at time t=0 (a) and the trial function corresponding to at time t=0 (b). Models of surface shell conductance on 𝕊a and absolute value of Bmain on 𝕊a used for the generation of the trial functions (c, d).
The corresponding vectorial Abel–Poisson kernel is simply defined by
Further calculations show
A spatially localized alternative to could then be defined by the set of functions , where is a fixed set of adequately distributed nodal points.
2.3 Spherical Slepian functions
While the localization of Abel–Poisson kernels is of radially symmetric nature, one is often interested in regions of more complex geometry, e.g., continents or oceans. Spherical Slepian functions, for instance, provide an orthonormal system of functions that can reflect localization in such general predefined regions Γ⊂𝕊 (see, e.g., Plattner and Simons, 2015, 2017a; Simons and Plattner, 2015; Simons et al., 2006 for details).
Specifically, the function f showing the best localization in Γ, is the one that maximizes the energy ratio
i.e., the one with an energy ratio closest to 1. Let us now assume that g(i) is a bandlimited vectorial function of type i with bandlimit N; i.e., it can be expanded as
Further, the matrix contains (properly sorted2) all of the appearing inner products
and , with and . If we now restrict ourselves to normalized functions g(i) (i.e., ), one obtains the simple expression . Eventually, the maximization of the energy ratio Eq. (8) leads to the eigenvalue problem
The eigenvalues λℓ are the possible energy ratios and the corresponding eigenvectors contain the Fourier coefficients of bandlimited functions attaining the energy ratio . The set of functions is ordered such that .
In typical scenarios, it turns out that the eigenvalues are clustered close to 1 and close to zero. Those eigenvalues which are closer to 1 determine the subset of well-localized Slepian functions that should be used for approximation in Γ. The code for the generation of vectorial Slepian functions has been kindly supplied in Plattner and Simons (2017b). For our situation, where Γ denotes the region of (a spherical) Earth which is covered by oceans, an illustration is provided in Fig. 2.
2.4 Physics-based trial functions
We start with the time-harmonic Maxwell equations as already indicated in Eq. (1). For simplicity, we assume a 1-D (only radially varying) conductivity model for σ within the ball 𝔹a, and at the surface 𝕊a we allow a laterally varying conductivity (cf. the bottom left image in Fig. 3 for an illustration). Further, the magnetic field Bmain is taken from the CHAOS-5 model (see Finlay et al., 2015) and u is supposed to denote a depth-integrated velocity field that is restricted to 𝕊a (in fact, within the numerical framework of the X3DG solver, we assume a constant ocean depth of 1km, with u being tangential to the sphere and independent of the depth). Since we are mainly interested in tidal velocity fields, it is a reasonable assumption that u is surface-divergence-free for most parts of the oceans. The latter means that u can be expanded in terms of vector spherical harmonics or vectorial Slepian functions of type 3, i.e., or , respectively.
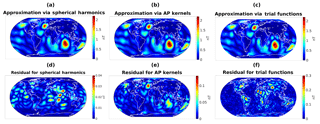
Figure 6Absolute value of the radial part of approximations of based on dictionary 𝒟1 (a), dictionary 𝒟2 (b), and dictionary 𝒟3 (c), as well as the corresponding residuals with respect to (d, e, f). Note the different scales in the bottom row which are chosen in order to emphasize the spatial distribution of the residuals.
For the generation of the tailored trial functions , we therefore substitute u by a set of surface-divergence-free functions that reflect spatial localization within the oceans. More precisely, we choose
where is the ℓth best localized vectorial Slepian function of type 3. The corresponding solution Boc of Eq. (1) within this setup then provides an auxiliary function . It should be noted that in order to obtain Maxwell's equation in the time-harmonic form Eq. (1), one has to apply a Fourier transform in time. Therefore, for the actual trial function Bℓ, we have to invert the Fourier transform and get
For technical reasons, we choose to work in a real-valued framework, so that the real and imaginary part of Bℓ each yield a trial function
Thus, each choice of uℓ yields two functions and that reflect the temporal periodicity of the tidal magnetic field as well as the spatial localization of the sources within the oceans. An illustration for the M2 tide with can be found in Fig. 3. For the computation of the as solutions of Eq. (1), we have used the X3DG solver from Kuvshinov (2008).
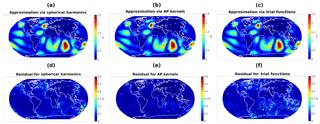
Figure 7Absolute value of the radial part of approximations of based on dictionary 𝒟1 (a), dictionary 𝒟2 (b), and dictionary 𝒟3 (c), as well as the corresponding residuals with respect to (d, e, f).
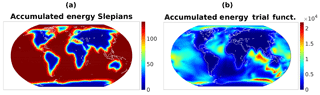
Figure 4 shows the accumulated energy , for ξ∈𝕊, of the underlying functions uℓ that describe the velocity field and the accumulated energy , for x∈𝕊r with km and time t=0, of the corresponding trial functions. In both cases, one can clearly see the spatial localization over the oceans. However, the accumulated energy of the trial functions additionally reflects the influence of the conductivity σ and the main/core magnetic field Bmain indicated in Fig. 3.
For our experiments we rely on the CM5 geomagnetic field model (cf. Sabaka et al., 2015) and a forward model based on the M2 depth-integrated tidal velocity field from TPXO8-ATLAS (cf. Egbert and Erofeeva, 2002) that has also been used in Kuvshinov (2008). The contribution of CM5 that is due to the oceanic M2 tide is given as an expansion in terms of spherical harmonics up to degree 18; we denote it as for the remainder of this section and sample it at M=250 000 points which are taken from actual Swarm satellite tracks. The forward model has been computed via the X3DG solver based on the surface conductance and the main/core magnetic field model indicated in the bottom row of Fig. 3 and a depth-integrated M2 tidal velocity field from TPXO8-ATLAS. We denote it by and evaluate it on the same point grid as before. These samples are used as input data b∈ℝM for the Regularized (Orthogonal) Functional Matching Pursuit, which works iteratively as indicated in Eq. (2). In the following, we want to illustrate the influence of the choice of different function systems (i.e., the choice of different dictionaries 𝒟) on the approximation of and . For that purpose, we choose three different dictionaries: the spherical-harmonic-based
with and the functions hn,k from Eq. (6); the Abel–Poisson-kernel-based
where a=6371.2 km, is a Reuter grid on 𝕊 with Mp=6201 nearly equally distributed points (see, e.g., Michel (2013), p. 137), and k given as in Eq. (7); and
with and , the physics-based trial functions from Eqs. (9) and (10).
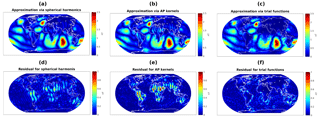
Figure 9Absolute value of the radial part of approximations of superposition based on dictionary 𝒟1 (a), dictionary 𝒟2 (b), and dictionary 𝒟3 (c), as well as the corresponding residuals with respect to original without the continental “noise” e (d, e, f).
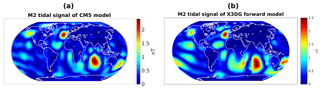
The actual signals that we want to approximate are indicated in Fig. 5. The approximations of together with the residuals for each of the three dictionaries above are shown in Fig. 6, whereas the respective approximations of and corresponding residuals are displayed in Fig. 7.

Table 1Root mean square errors (RMSEs) corresponding to the approximations of the undisturbed forward model as well as the noisy model compared to the “ground truth” with the three different dictionaries. Left-hand columns show errors for the approximation of (compare Fig. 7), while center columns show errors for the approximation of (compare Fig. 9). The right-hand columns display the RMSEs of the difference between the respective approximations (as shown in Fig. 10).

In the case of as the underlying signal, it can be seen in Fig. 6 that the dictionary 𝒟1 yields the overall best approximation, which, however, is not surprising since we try to fit a spherical-harmonic-based model with a spherical-harmonic-based dictionary. The result for dictionary 𝒟2 shows a more localized pattern in the residual, as is expected for the use of Abel–Poisson kernels. However, the maxima in the residual are not correlated to specific continental or oceanic structures but they mainly coincide with the maxima of the original signal . The situation for dictionary 𝒟3 of physics-based trial functions is different. The agreement of the approximation with is good over the oceans but significant deviations exist over the continents. The latter could be an indication that the original model contains contributions over the continents whose physical origin is not due to induction by oceanic tides. Some smaller deviations over oceanic areas exist around southern Africa and the east of Australia. Since we are dealing with the approximation of a low-degree (up to degree 18) spherical-harmonic-based M2 tidal magnetic field model by localized trial functions, one cannot reliably say if the latter deviations are artifacts from the approximation procedure or if they have a physical origin. However, those are areas with a shallower ocean topography, so the assumption of surface-divergence-free depth-integrated tidal velocities (which we made for our choice of the underlying uℓ) and the assumption of a constant ocean depth (we chose a depth of 1 km for the generation of the via the X3DG solver) might not be accurate in these areas. Nonetheless, the residuals over the continents show that the use of the adapted trial functions might eventually deliver improved tidal magnetic field models that correct unrealistic continental contributions without disregarding continental areas entirely.
The residuals of the approximations of the forward model in Fig. 7, on the other hand, indicate that the quality of the approximations does not vary too much (at least on scales that are relevant for satellite data approximation) among the three tested function systems. This is mainly due to the fact that the input model already reflects certain spatial localization properties over the oceans. In such a scenario (if additionally solely interested in the approximation of the signal and not the underlying velocity fields) it would, therefore, not be necessary to use the adapted trial functions that we have introduced. The crucial point, however, is that satellite data typically contain undesired contributions over the continents that are not due to ocean-tide-generated magnetic fields. In order to illustrate this behavior, we use the following additional example. We take randomly distributed Fourier coefficients to construct a “noise” function e with a bandlimit of degree 40, i.e.,
where the Fourier coefficients are normally distributed with zero mean and a variance such that the amplitude of e is in the range of the oceanic signal . This function e is then restricted to the continents and eventually superposed with the forward model (cf. Fig. 8). For the sake of clarity, we denote the approximations of the noisy data
by instead of . The latter still represents the approximation of without extra continental noise e.
In Fig. 9 one can directly see the influence which the continental noise has on the approximation depending on the various dictionaries (Fig. 7 shows the same quantities for the approximations in the undisturbed setup). In the case of dictionary 𝒟1, the spherical harmonics also approximate a part of the continental data which in turn also has some impact on the approximation in oceanic areas. Due to the localization of the kernels contained in dictionary 𝒟2, the (undesired) reconstruction of the continental noise is even more accurate, while the reconstruction over the oceans only changes very slightly. With the proposed physics-based functions in dictionary 𝒟3, however, the influence of the continental noise is much less apparent. The maxima occur very close to the coastline, which is most likely due to numerical issues stemming from discontinuities of the data in coastal areas. A closer look at the differences between the approximations of noisy and undisturbed data is given in Fig. 10. This shows again that the inclusion of continental noise has a smaller effect on the approximation via physics-based trial functions than on the approximations via the other tested trial functions. Moreover, the corresponding root mean square errors of the approximations and , respectively, can be found in Table 1. In both cases, we compared the approximations to the undisturbed data in order to emphasize the impact of continental noise on the overall approximation. The errors over continental and oceanic regions are provided separately.
The main goal of this paper is to study the errors that are made by the approximation of tidal magnetic fields by use of different sets of trial functions. While, e.g., Saynisch et al. (2018) compared forward models for the M2 tidal magnetic field based on different tidal models, we aim at illustrating the effect of the involved trial functions on the possible extraction of the tidal magnetic field from satellite data in the first place. The indicated residuals for the synthetic examples show that the use of the presented adapted physics-based trial functions could have a detectable effect for the extraction of such signals in satellite data. These trial functions reflect the underlying physics in the sense that they satisfy the time-harmonic Maxwell equations and that they include knowledge of the ambient core magnetic field and the Earth's conductivity, but they are not designed to rely on detailed oceanographic models. The latter can be advantageous since the extracted magnetic field induced by ocean tides might eventually be used to make inferences on such models.
The authors would like to thank the following providers of software and models: Alexey Kuvshinov for the code of the X3DG solver and a processed version of the depth-integrated tidal ocean velocities from TPXO8-ATLAS, Nils Olsen for the coefficients of the M2 tidal contribution in the CM5 model, Alain Plattner for the code for the generation of vectorial Slepian functions.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Dynamics and interaction of processes in the Earth and its space environment: the perspective from low Earth orbiting satellites and beyond”. It is not associated with a conference.
This work was supported by DFG grant GE 2781/1-1 within the Research Priority
Program SPP 1788 “DynamicEarth”.
Edited by:
Juergen Kusche
Reviewed by: two anonymous referees
Egbert, G. and Erofeeva, S.: Efficient inverse modeling of barotropic ocean tides, J. Atmos. Ocean Tech., 19, 183–204, 2002. a
Finlay, C., Olsen, N., and Tøffner-Clausen, L.: DTU candidate field models for IGRF-12 and the CHAOS-5 geomagnetic field model, Earth Planet. Space, 67, 114–130, 2015. a
Fischer, D. and Michel, V.: Automatic best-basis selection for geophysical tomographic inverse problems, Geophys. J. Int., 193, 1291–1299, 2013. a
Freeden, W. and Gerhards, C.: Geomathematically Oriented Potential Theory, Pure and Applied Mathematics, Chapman & Hall/CRC, 468 pp., 2012. a
Freeden, W., Gervens, T., and Schreiner, M.: Constructive Approximation on the Sphere (With Applications to Geomathematics), Oxford Science Publications, Clarendon Press, 444 pp., 1998. a
Grayver, A., Schnepf, N., Kuvshinov, A., Sabaka, T., Manoj, C., and Olsen, N.: Satellite tidal magnetic signals constrain oceanic lithosphere-asthenosphere boundary, Sci. Adv., 2, e1600798, https://doi.org/10.1126/sciadv.1600798, 2016. a
Irrgang, C., Saynisch, J., and Thomas, M.: Impact of variable seawater conductivity on motional induction simulated with an ocean general circulation model, Ocean Sci., 12, 129–136, https://doi.org/10.5194/os-12-129-2016, 2016. a
Kuvshinov, A.: 3-D Global Induction in the Ocean and Solid Earth: Recent Progress in Modeling Magnetic and Electric Fields from Sources of Magnetospheric, Ionospheric, and Ocean Origin, Surv. Geophys., 29, 139–186, 2008. a, b, c
Kuvshinov, A. and Olsen, N.: 3-D Modeling of the Magnetic Fields due to Ocean Tidal Flow, in: Earth Observation with CHAMP, Results from Three Years in Orbit, edited by: Reigber, C., Lühr, H., Schwintzer, P., and Wickert, J., Springer, 2005. a
Malin, S.: Separation of Lunar Daily Geomagnetic Variations into Parts of Ionospheric and Oceanic Origin, Geophys. J. R. Astr. Soc., 21, 447–455, 1970. a
Michel, V.: Lectures on Constructive Approximation – Fourier, Spline, and Wavelet Methods on the Real Line, the Sphere, and the Ball, Birkhäuser, 2013. a
Michel, V. and Telschow, R.: A non-linear approximation method on the sphere, GEM – Int. J. Geomath., 5, 195–224, 2014. a
Michel, V. and Telschow, R.: The regularized orthogonal functional matching pursuit for ill-posed inverse problems, SIAM J. Numer. Anal., 54, 262–287, 2016. a
Plattner, A. and Simons, F.: Spatiospectral concentration of vector fields on a sphere, Appl. Comp. Harm. Anal., 36, 1–22, https://doi.org/10.1016/j.acha.2012.12.001, 2014. a
Plattner, A. and Simons, F.: Potential-field estimation from satellite data using scalar and vector Slepian functions, in: Handbook of Geomathematics, edited by: Freeden, W., Nashed, M., and Sonar, T., Springer, 2nd Edn., 2015. a, b
Plattner, A. and Simons, F.: Internal and External Potential-Field Estimation from Regional Vector Data at Varying Satellite Altitude, Geophys. J. Int., 211, 207–238, 2017a. a
Plattner, A. and Simons, F.: csdms-contrib/slepian_golf: Centennial, https://doi.org/10.5281/zenodo.583627, 2017b. a
Sabaka, T., Olsen, N., Tyler, R., and Kuvshinov, A.: CM5, a pre-Swarm comprehensive geomagnetic field model derived from over 12 years of CHAMP, Ørsted, SAC-C and observatory data, Geophys. J. Int., 200, 1596–1626, 2015. a, b, c
Sabaka, T., Tyler, R., and Olsen, N.: Extracting ocean-generated tidal magnetic signals from Swarm data through satellite gradiometry, Geophys. Res. Let., 43, 3237–3245, 2016. a
Saynisch, J., Irrgang, C., and Thomas, M.: Estimating ocean tide model uncertainties for electromagnetic inversion studies, Ann. Geophys., 36, 1009–1014, https://doi.org/10.5194/angeo-36-1009-2018, 2018. a, b
Schnepf, N., Kuvshinov, A., and Sabaka, T.: Can we probe the conductivity of the lithosphere and upper mantle using satellite tidal magnetic signals?, Geophys. Res. Let., 42, 3233–3239, 2015. a
Simons, F. and Plattner, A.: Scalar and vector Slepian functions, spherical signal estimation and spectral analysis, in: Handbook of Geomathematics, edited by: Freeden, W., Nashed, M., and Sonar, T., Springer, 2nd Edn., 2015. a
Simons, F., Dahlen, F., and Wieczorek, M.: Spatiospectral localization on a sphere, SIAM Review, 48, 505–536, 2006. a
Tyler, R., Maus, S., and Lühr, H.: Satellite Observations of Magnetic Fields due to Ocean Tidal Flow, Science, 299, 239–240, 2003. a