the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Meteor echo height ceiling effect and mesospheric temperature estimation from meteor radar observations
Geonhwa Jee
Jeong-Han Kim
In-Sun Song
The mesospheric temperature estimation from meteor height distribution is reevaluated by using the Sounding of the Atmosphere using Broadband Emission Radiometry (SABER) and the King Sejong Station (KSS) meteor radar observations. It is found that the experimentally determined proportionality constant between the full width at half maximum (FWHM) of the meteor height distribution and temperature is in remarkable agreement with theoretical value derived from the physics-based equation and it is nearly time-invariant for the entire observation period of 2012–2016. Furthermore, for the first time we found that the FWHM provides the best estimate of temperature at slightly lower height than the meteor peak height (MPH) by about 2–3 km. This is related to the asymmetric distribution of meteor echoes around MPH, which is known to be caused by the meteor echo height ceiling effect (MHC). At higher altitude above MPH, the meteor detection rate is greatly reduced due to the MHC, and the cutoff height for this reduction follows a fixed molecular mean free path of the background atmosphere. This result indicates that the meteor height distribution can be used to estimate the mesospheric temperature, even under the asymmetric meteor echo distribution caused by the MHC at high altitude.
Key points:
-
Representative altitude of temperature estimated from the full width at half maximum (FWHM) is slightly lower than the meteor peak height by about 2–3 km.
-
The meteor echo height ceiling effect (MHC) creates remarkable asymmetry in the height profile of the correlation between the FWHM and layer mean temperature.
-
The state of the background atmosphere is intrinsically reflected in the MHC and therefore in the observed FWHM.
Recent advances in the performance of meteor radar have enabled continuous observations for the daily mesospheric temperature and hourly neutral winds in the mesosphere and lower thermosphere region. As meteoroids enter the earth's atmosphere, they undergo ablation due to collisional heating with atmospheric constituents, leaving cylindrical ionized meteor trails behind them. By observing these meteor trails with a meteor radar, one can extract a variety of essential information on the background atmosphere as well as the meteors (McKinley, 1961; Ceplecha et al., 1998; Holdsworth et al., 2004). While the neutral winds can be directly obtained from the measurement of Doppler shift of backscattered signals, the temperature near the mesopause region has been conventionally estimated from the diffusion coefficients of underdense meteor echoes based on the dependence of the diffusion coefficient on the atmospheric temperature and pressure (Tsutsumi et al., 1994; Chilson et al., 1996; Kim et al., 2012, and references therein). However, Eshleman (1957) provided a theoretical basis for the relationship between the atmospheric density scale height and the height range of detected meteor echoes. This relationship was developed by showing that the width of the height distribution of detected meteors is a nearly linear function of the density scale height (Younger, 2011). Lee et al. (2016) demonstrated that there is a clear linear relationship between the FWHM of the height distribution of detected meteor echoes and the temperature retrieved from the Aura Microwave Limb Sounder (MLS) based on a basic theory and observations. They further showed that the temperature estimated from this relation is in better agreement with satellite temperature measurements compared with conventionally estimated temperature from meteor decay times. Although it was successfully shown that meteor height distribution provides mesospheric temperature, the MLS temperature data have a poor height resolution (∼10 km), which is nearly comparable to the FWHM in the mesosphere. Therefore, the resulting temperature from the FWHM was assumed to be a layer mean temperature near the meteor peak height (MPH). Furthermore, a meteor radar has a limitation on the height range of meteor detection; it depends on radar specifications such as a pulse repetition frequency and a radio wavelength (Cervera and Reid, 2004).
In this study, we reexamine the temperature estimation procedure from the FWHM with the emphasis of the invariance of the proportionality constant between the FWHM and background temperature, not only from theoretical consideration but also from meteor radar and TIMED/SABER (Sounding of the Atmosphere using Broadband Emission Radiometry instrument on NASA's Thermosphere Ionosphere Mesosphere Energetics Dynamics satellite) observations. In addition, we also evaluate the validity of temperature estimation from the FWHM under the MHC. The meteor radar observations at King Sejong Station (KSS) and the TIMED/SABER instrument are briefly introduced in Sect. 2. Section 3 describes a theoretical derivation of the linear relationship between the FWHM and background temperature. The results of this study are presented in Sect. 4 with relevant discussions. Finally, this is followed by a conclusion in Sect. 5.
2.1 King Sejong meteor radar
Meteor radar has been used to continuously monitor atmospheric winds and temperatures in the mesosphere and lower thermosphere for several decades. The Korea Polar Research Institute (KOPRI) has operated a meteor radar at KSS in Antarctica (62.22∘ S, 58.78∘ W) in collaboration with Chungnam National University, South Korea, since March 2007. The KSS meteor radar, with a frequency of 33.2 MHz, transmits 7.2 km width, 4-bit complimentary coded circularly polarized pulses at a pulse repetition frequency of 440 Hz. The transmitter has a peak power of 12 kW and a duty cycle of 8.4 %. The receiver is composed of two perpendicular interferometric baselines as a standard antenna configuration (Jones et al., 1998) to determine the angle of arrival of backscattered signal from meteor trails (Holdsworth et al., 2004; Lee et al., 2013).
It collects underdense meteor echoes within a horizontal radius of about 250 km from the radar site. The number of meteor echoes from the KSS meteor radar reaches up to 40 000 meteors per day in summer but it declines to about 15 000 in winter. The large number of meteor echoes enables us to obtain reliable meteor samples even beyond the typical meteor detection height of 80–100 km with a better temporal resolution.
In this study we used 5-year-long meteor radar data from 2012 to 2016 to ensure better statistics of meteor distribution, even under the minimized meteor detection rate in winter. The phase difference error of meteor echoes derived from six receive antenna pairs is limited to be less than 6∘ to determine the most accurate meteor height distribution. In deriving a linear relationship between the width of meteor height distribution and the SABER temperature, the geometric height of meteor echoes was converted to geopotential height in order to correctly compare it with the proportionality constant derived from the fundamental hydrostatic equation.
2.2 TIMED/SABER
The Sounding of the Atmosphere using Broadband Emission Radiometry (SABER) instrument is one of four instruments on NASA's TIMED (Thermosphere Ionosphere Mesosphere Energetics Dynamics) satellite to measure the limb emission in the 10 broadband infrared channels covering 1.27 to 17 µm. The profile of kinetic temperature is obtained from the 15 µm radiation of CO2 from 15 to 120 km altitude.
The SABER instrument views the atmospheric limb perpendicular to the satellite orbital track in an altitude of about 625 km and an inclination of 74∘. In order to keep the SABER instrument on the anti-sunward side, the TIMED satellite performs yaw maneuvers about every 60-day period. Consequently, the latitude coverage on a given day extends from about 52∘ in one hemisphere to 83∘ in the other, and this results in only 6 months of SABER data available every year in high-latitude regions above 52∘. The height resolution of the data varies with altitude and it is about 2 km in the region of meteor detection. The SABER data used in this study are version 2.0, which includes non-LTE (non-local thermodynamic equilibrium) temperature inversions in the upper mesosphere and lower thermosphere due to the departure from LTE in the CO2 15 µm vibration–rotation band for the kinetic temperature determination above 70 km altitude (Mertens et al., 2001, 2004). The SABER temperature and geopotential height data were restricted to the distance of less than 500 km from the location of KSS to directly compare with the FWHM derived from meteor radar observations during the period of 2012–2016.
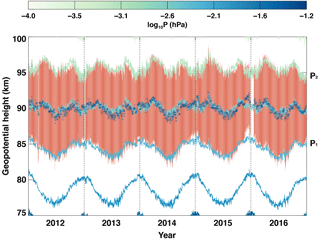
Figure 1Temporal evolution of constant pressure surfaces of the neutral atmosphere from Aura MLS (both filled and line contours) and meteor peak detection heights (blue open diamond) with full width at half maximum (FWHM) of meteor height distribution (red shaded area) from meteor radar observations at King Sejong Station, Antarctica, in 2012–2016. Two constant atmospheric pressure (P1, P2) levels that are strongly correlated with the FWHM are also presented.
According to Lee et al. (2016), most of the observed underdense meteor echoes show specific height distributions being primarily determined by background atmospheric pressure. Figure 1 shows the MPH (blue open squares) and FWHM (red-shaded area) obtained from the fitting procedure with a Gaussian curve applied to the daily meteor height distribution from 2012 to 2016. The background atmospheric pressure field from the MLS measurement is also presented by solid line contours. It is important to note that the MPH closely follows the constant pressure level and a fixed portion of the height distribution (i.e., FWHM) of observed meteor echoes exists within two constant pressure levels around the MPH as shown in Fig. 1. As meteors penetrate into the Earth's atmosphere down to about 120 km height, they produce meteor trails, which are composed of metallic ions and electrons by collisions with atmospheric constituents (Love and Brownlee, 1991; Rogers et al., 2005). This collisional heating process is critically affected by background atmospheric pressure, which is a function of density and temperature. Therefore, the height distribution of meteor echoes, represented by the FWHM, is determined by the state of the background atmosphere.
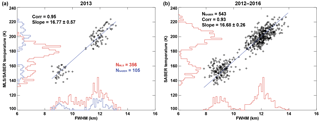
Figure 2Scatter plots of the daily FWHM of the meteor height distribution versus the average value of the SABER temperatures near the mesopause region at King Sejong Station in (a) 2013 and (b) the 5 years from 2012 to 2016. The blue solid line depicts the linear regression. The histograms of the two independent temperature measurements from the SABER (blue) and MLS (red) and FWHM data are also presented to show the number of data used in the linear least squares.
The linear relationship between the FWHM and temperature can be derived from the conventional atmospheric statics; the variation of pressure with height can be determined from the ideal gas law and the hydrostatic equation (Andrew et al., 1987):
where g and R are the gravitational acceleration and gas constant, respectively. After a simple rearrangement for separation of variables, both sides in Eq. (1) can be integrated over the region between two given constant pressure levels of P1(Z1) and P2(Z2) to obtain the hypsometric equation:
The height difference Z2−Z1 in Eq. (2) corresponds to an atmospheric layer between the two constant pressure levels. Since the FWHM of the meteor height distribution nearly coincides with the atmospheric layer as in Fig. 1, it can be used to estimate the mean temperature of the layer from Eq. (2):
where and the proportionality constant . Here the layer mean temperature is defined as
As is revealed from the definition of the layer mean temperature given by Eq. (4), the mean temperature can be defined for any kind of temperature profile, even a vertically rapidly varying temperature structure in the atmosphere.
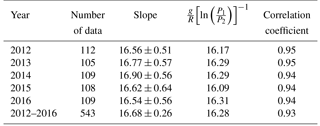
Equation (3) clearly shows that the neutral temperature near the meteor peak height can be determined by the FWHM alone with a proportionality constant. The constant can be empirically determined based on a linear relationship between the observed FWHM and temperature. It turns out that the determined proportionality constant does not vary with time and can be considered to be a “constant” over the entire observation period. The constant can also be estimated with pressure measurements from SABER observations. From 5-year averaged values of , from the SABER pressure measurements during the period of 2012–2016, the ratio between two pressure levels, P1 / P2, is determined to be 7.59. Then the proportionality constant in Eq. (3) can be estimated to be about 16.28 when the gravitational constant g and gas constant R are approximately 9.47 and 287.06, respectively, in the region of given pressure levels of P1 and P2 near 90 km altitude. In the following section, we will empirically determine the constant using the measurements of FWHM and temperature and will compare it with the estimated constant from the pressure measurements.
4.1 Empirical estimation of the proportionality constant
Using the FWHM and temperature measured from the KSS meteor radar and SABER, respectively, we can determine the proportionality constant during the period of 2012–2016. Figure 2 shows the scatter plots of the daily FWHMs derived from the KSS meteor radar versus the TSABER at around 87 km for the year of 2013 (a) and for the entire observation period of 2012–2016 (b). In contrast to MLS temperature data used in our previous study (Lee et al., 2016), SABER temperature measurements above KSS are only available in its south viewing geometry due to yaw maneuvers about every 60 days. This observational limitation gives rise to fewer temperature data points available for the determination of the proportionality constant, which is why there are few data points in the middle of the scatterplot in Fig. 2. Nevertheless, it has a much better height resolution than MLS temperature measurement: the height resolution of SABER observations is about 2 km, while the resolution of MLS observations is about 10–13 km, which is almost comparable to the FWHM. This characteristic of SABER observations allows us to find the representative altitude of the estimated temperature from the FWHM (Liu et al., 2017).
There is an obvious linear relationship between TSABER and FWHM with notably high correlation coefficients. The slopes in Fig. 2 represent the proportionality constant between the FWHM and TSABER. Table 1 shows yearly slopes during the 5-year observation period. Note that the slopes are almost invariable within the associated error ranges during the entire observation period of 2012–2016. They also agree well with the proportionality constant in Eq. (3) with SABER pressure measurements. Lee et al. (2016), using the Aura/MLS temperature data, obtained a notably smaller slope value of 15.71 with a worse correlation coefficient between the FWHM and temperature, which might be due to the poor height resolution of MLS temperature data in the mesosphere and lower thermosphere region. It should be emphasized that the essential point of this procedure is the invariance of the proportionality constant between the FWHM and temperature near the MPH. Therefore, once it is determined from the independent measurement of temperature, it can be used to estimate the temperature from the meteor radar observations of the FWHM alone without any additional assumed parameter.
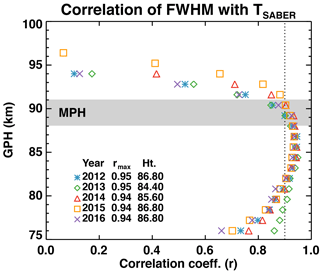
Figure 3The height profile of correlation coefficient of the FWHM and SABER temperatures in 2012–2016. The height information of the maximum correlation coefficient and its value in each year are also summarized. The dotted vertical line indicates a correlation coefficient of 0.9, and the gray shaded box denotes the height range of the MPH variation during the observation period.
4.2 Meteor echo height ceiling effect on the temperature estimation
The estimated temperature using Eqs. (2)–(4) is the mean temperature between the two constant pressure levels as shown in Fig. 1. It therefore seems plausible that the mean temperature represents the temperature at around the meteor peak height (MPH) for the pressure levels around the FWHM. In order to confirm this representative altitude of the estimated temperature with the FWHM, we performed a correlation analysis between the FWHM and layer mean temperatures at different altitudes. Figure 3 shows the height profiles of the correlation coefficient between the FWHM and SABER temperature during the period of 2012–2016. For this analysis, the SABER temperatures were averaged at every 1.2 km of height within 2.4 km width to obtain daily layer mean temperatures for each year. It is clear in the figure that the best correlation occurs at a slightly lower height (∼87 km) than the MPH (88–91 km) by about 3–4 km. The temperature estimation procedure using the meteor decay times, however, assumed that the representative altitude of the estimated temperature is around the meteor peak height, which is about 90 km altitude (Kim et al., 2012; Meek et al., 2013). A notable asymmetry in the correlation coefficients around the maximum correlation height is another important feature in Fig. 3. The correlation coefficient more rapidly decreases at the altitude above the MPH than below, and this indicates that the meteor height distribution above the MPH is not only controlled by the background atmospheric state but other factors must also be involved.
The height distribution of meteor echoes detected by meteor radar depends not only on the physical characteristics of meteors and the state of the atmosphere but also on the operational parameters of meteor radar such as a radio wavelength and a pulse repetition frequency. Meteor radar observations show a limited height range of detecting meteors for a given radio wavelength. The backscattered signals from meteor trails beyond this range are significantly attenuated to be detected (Thomas et al., 1988; Steel and Elford, 1991). This limitation is inherently present in the meteor radar observations, which is known as the meteor echo height ceiling effect (MHC). Immediately after meteor ionized trails are formed, they rapidly expand in a radial direction to reach a finite radial extent called an initial radius within the interval that meteoric ions are in thermal equilibrium with surrounding atmosphere (Jones, 1995). As the atmospheric density decreases with increasing height, the initial radius of the meteor trail is increased and becomes greater than a quarter of the radio wavelength, which significantly attenuates echo strength due to the lack of phase coherence from the signals reflected from the different spots in the meteor trail cross-section (Younger et al., 2008). In general, the meteor trails from fast meteors are produced at higher altitudes, and hence meteor radar observations miss the significant part of meteors above a certain altitude because of the MHC (McKinley, 1961; Campbell-Brown and Jones, 2003).
According to the echo attenuation theory, there are three major factors controlling the attenuation in the amplitude of meteor echoes from underdense meteor trails. Previous studies reviewed these attenuation factors and quantified their influences on the MHC (Thomas et al., 1988; Steel and Elford, 1991). Since the detailed examination of three attenuation factors is beyond the scope of this study, we only give a brief overview of them and find which one is the most important in meteor echo attenuation. The reduced electron density and its weighting function (zeroth-order Bessel function) oscillating in positive and negative regions with a radial distance in the meteor trail with a larger initial radius makes the backscattered signal too weak to be detected by radars (initial radius factor, αr) (McKinley, 1961; Younger et al., 2008). The signal attenuation is also generated by the diffusion during the time of meteor trail formation due to the finite velocity of the meteoroid (finite velocity factor, αV). If the inter-pulse period of a meteor radar is comparable to or longer than the meteor decay times, it is more likely that the meteor trail detected by one pulse decays below the threshold of meteor recognition before the arrival of a successive pulse (pulse repetition rate factor, αP).
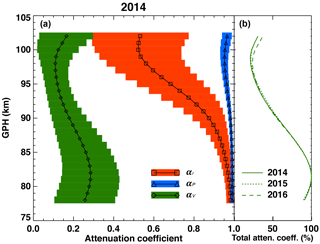
Figure 4(a) The height variation of the three yearly mean attenuation coefficients and their 1 standard deviation values (color-filled horizontal bars) calculated from the KSS meteor radar observations in 2014, and (b) the normalized percentage of yearly mean total attenuation coefficients in 2014–2016.
In the temperature estimation procedure using the FWHM of meteor height distribution, it is critically important to take account of the MHC caused by these attenuation factors in the meteor radar observations. Although it is the background atmospheric pressure field primary factor to determine the FWHM, the MHC also contributes to the FWHM by reducing the detection of high-altitude meteor trails. It should be noted that proportionality constants derived from a least-squares method using the SABER temperature and the FWHM are slightly larger (1.4 %–3.7 %) than values from Eq. (3) with SABER pressure measurements as shown in Table 1. The underestimated FWHM due to the MHC probably makes a systematic difference between the two constants over the entire observational period. In this study, we calculated the three attenuation coefficients using key parameters obtained from meteor radar observations to examine how much the FWHM can be affected by the MHC and how it can influence the temperature estimation.
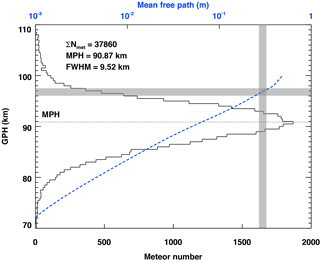
Figure 5The histogram of a meteor height distribution observed by the KSS meteor radar on a single day in 2016 using a 500 m bin. The blue dashed line presents the mean free path of the background atmosphere calculated from the MLS observations. The gray-colored horizontal bar indicates the height layer where a rapid decrease in meteor detection rate due to the meteor echo height ceiling appears. The typical range of the molecular mean free path that activates the meteor echo height ceiling due to the initial radius and finite velocity factors is depicted by a gray-colored vertical bar.
We applied an attenuation theory described in Steel and Elford (1991) and Ceplecha et al. (1998) to the KSS meteor radar data to calculate the attenuation coefficients. Figure 4 presents the height profiles of three attenuation coefficients with standard deviations calculated from the data in 2014. Because the KSS meteor radar has a large pulse repetition frequency, the inter-pulse period is much shorter than decay times of most observed underdense meteor trails. Hence, the pulse repetition rate factor (blue filled triangle) should be negligible in the meteor signal attenuation throughout all the altitude region, and the net attenuation of meteor echoes is dominated by αr and αV as depicted in Fig. 4. The αr, in particular, dramatically decreases as the initial radius (r0) increases with height. This indicates that the amplitude of radar signals scattered from meteor trails is severely declined at higher altitudes above about 95 km. As for the finite velocity factor, αV, since it is basically related to the background atmospheric state, the height variation of αV remarkably coincides with that of meteor decay times, which steadily decreases with height because of the exponential decrease of the background pressure within about 82–97 km altitude range (Singer et al., 2008; Kim et al., 2010). As shown in Fig. 4, the MHC generated by αr and αV reaches maximum (i.e., minimum attenuation coefficients) at about 100 km, and this altitude is known to be a typical cutoff height for 30 MHz meteor radar observations, representing the limitation height of the observations (Olsson-Steel and Elford, 1987; Thomas et al., 1988). Because of this MHC, signals backscattered from meteor trails are significantly attenuated at higher altitudes, which causes far worse correlations between the height distribution of meteor echoes and the background atmospheric temperatures as shown in Fig. 3.
According to Fig. 4, we found the MHC for the KSS meteor radar is primarily controlled by the initial radius and finite velocity factors. If we assume that the distribution of meteor speed does not vary much over the 5-year observation period, the two major attenuation processes should mainly be affected by the background atmospheric density. Since the molecular mean free path is inversely proportional to the atmospheric density, it is more intuitive to describe the relation between the background atmosphere and the initial radius. Figure 5 illustrates the height distribution of meteor echoes recorded on a single day in 2016 and the height profile of the molecular mean free path calculated from the MLS pressure measurement. Note that the number of meteor echoes observed at a given height bin above the MPH more rapidly decreases with height than below. Jones and Campbell-Brown (2005) showed that the initial radius of meteor trails is about 1–2 m at the altitude of 95 to 100 km for a meteoroid falling with a speed of 40 km s−1, and they deduced a relationship between meteor speed V and the initial radius ri : . The molecular mean free path is approximately one-third of the initial radius (Manning, 1958). When the MHC is most effective at around 97 km altitude (see Fig. 5), the mean free path is about a few tens of centimeters with the initial radius of about 2–3 m, which corresponds to approximately a quarter of the wavelength of the KSS meteor radar (9.03 m). This indicates that the MHC occurs within a fixed range of the mean free path as shown in previous studies (Pellinen-Wannberg and Wannberg, 1994; Westman et al., 2004); in other words, it occurs in a certain atmospheric state. For the KSS meteor radar, the MHC mostly occurs at around 97 km altitude, which exists way above the MPH as shown in both Figs. 4 and 5. Consequently, it can be concluded that the MHC affecting meteor height distribution above the MPH is mainly controlled by the background atmospheric condition, and in turn, this provides an essential validation of the temperature estimation from the FWHM.
In this study, the temperature estimation procedure from the FWHM is reevaluated by verifying the temporal invariance of the proportionality constant between the FWHM and mesospheric temperature over the entire observation period of 2012–2016. Their linear relationship with a proportionality constant is experimentally demonstrated from the SABER temperature and meteor radar observations in the 5-year observation period. The slope of the SABER temperature and FWHM is more consistent with the theoretically derived proportionality constant than those from the MLS temperature in Lee et al. (2016). Compared to the MLS data, much better vertical resolution of the SABER temperature enabled us to find that the mesospheric temperature estimated from the FWHM represents the temperature at around 87±2 km altitude, which is slightly lower than the meteor peak height by about 2–3 km. The lower representative altitude of the estimated temperature results from the asymmetric meteor echo distribution, with much lower meteor detection rates above the MPH, which is caused by the meteor echo height ceiling effect (MHC). Since the MHC reflects the background atmospheric state well, the FWHM derived from the KSS meteor radar can be used to estimate mesospheric temperature accurately.
The TIMED/SABER data are available from the SABER data services by following the link: http://saber.gats-inc.com/data.php (last access: 12 May 2018). The Aura/MLS data can be accessed at the NASA GES DISC by following the link: http://disc.sci.gsfc.nasa.gov/Aura/data-holdings/MLS (last access: 12 May 2018). King Sejong meteor radar data are available from the Korea Polar Research Institute upon request.
CL developed the main idea of this study and prepared the manuscript. GJ is the principal investigator of the polar space environment research project. JK provided King Sejong meteor radar data. IS helped interpret the observational data. All the authors contributed to the discussion as a team effort.
The authors declare that they have no conflict of interest.
This study was supported by grant PE18020 from the Korea Polar Research
Institute. The authors would like to thank the TIMED SABER team for providing
the kinetic temperature and geopotential height (version 2.0)
data. The Aura MLS team is also gratefully
acknowledged for providing the geopotential height and pressure data.
The topical editor, Huixin Liu, thanks two anonymous referees for help in evaluating this paper.
Andrew, D. G., Holton, J. R., and Leovy, C. B.: Middle Atmosphere Dynamics, 498 pp., Academic, San Diego, California, 1987.
Campbell-Brown, M. and Jones, J.: Determining the initial radius of meteor trains: fragmentation, Monthly Notice of the Royal Astronomical Society, 343, 775–780, https://doi.org/10.1046/j.1365-8711.2003.06713.x, 2003.
Ceplecha, Z., Borovička, J. Í., Elford, W. G., ReVelle, D. O., Hawkes, R. L., Porubčan, V. Í., and Šimek, M.: Meteor phenomena and bodies, Space Sci. Rev., 84, 327–471, 1998.
Cervera, M. A. and Reid, I. M.: Comparison of atmospheric parameters derived from meteor observations with CIRA, Radio Sci., 35, 833–843, https://doi.org/10.1029/1999RS002226, 2000.
Chilson, P. B., Czechowsky, P., and Schmidt, G.: A comparison of ambipolar diffusion coefficients in meteor trains using VHF radar and UV lidar, Geophys. Res. Lett., 23, 2745–2748, https://doi.org/10.1029/96GL02577, 1996.
Eshleman, V. R.: The Theoretical Length Distribution of Ionized Meteor Trails, J. Atmos.-Terr. Phys., 10, 57–72, 1957.
Holdsworth, D. A., Reid, I. M., and Cervera, M. A.: Buckland Park all-sky interferometric meteor radar, Radio Sci., 39, RS5009, https://doi.org/10.1029/2003RS003014, 2004.
Jones, J. and Campbell Brown, M.: The initial train radius of sporadic meteors, Mon. Not. R. Astro. Soc., 359, 1131–1136, https://doi.org/10.1111/j.1365-2966.2005.08972.x, 2005.
Jones, J., Webster, A. R., and Hocking, W. K.: An improved interferometer design for use with meteor radars, Radio Sci., 33, 55–65, https://doi.org/10.1029/97RS03050, 1998.
Jones, W.: Theory of the initial radius of meteor trains, Mon. Not. R. Astro. Soc., 275, 812–818, 1995.
Kim, J.-H., Kim, Y. H., Lee, C. S., and Jee, G.: Seasonal variation of meteor decay times observed at King Sejong Station (62.22∘ S, 58.78∘ W), Antarctica, J. Atmos. Sol.-Terr. Phys., 72, 883–889, https://doi.org/10.1016/j.jastp.2010.05.003, 2010.
Kim, J.-H., Kim, Y. H., Jee, G., and Lee, C.: Mesospheric temperature estimation from meteor decay times of weak and strong meteor trails, J. Atmos. Sol.-Terr. Phys., 89, 18–26, https://doi.org/10.1016/j.jastp.2012.07.003, 2012.
Lee, C., Kim, Y. H., Kim, J.-H., Jee, G., Won, Y.-I., and Wu, D. L.: Seasonal variation of wave activities near the mesopause region observed at King Sejong Station (62.22∘ S, 58.78∘ W), Antarctica, J. Atmos. Sol.-Terr. Phys., 105, 30–38, https://doi.org/10.1016/j.jastp.2013.07.006, 2013.
Lee, C., Kim, J.-H., Jee, G., Lee, W., Song, I.-S., and Kim, Y. H.: New method of estimating temperatures near the mesopause region using meteor radar observations, Geophys. Res. Lett., 43, 10580–10585, https://doi.org/10.1002/2016GL071082, 2016.
Liu, L., Liu, H., Le, H., Chen, Y., Sun, Y.-Y., Ning, B., Hu, L., Wan, W., Li, N., and Xiong, J.: Mesospheric temperatures estimated from the meteor radar observations at Mohe, China, J. Geophys. Res.-Space, 122, 2249–2259, https://doi.org/10.1002/2016JA023776, 2017.
Love, S. G. and Brownlee, D. E.: Heating and thermal transformation of micrometeoroids entering the earth's atmosphere, Icarus, 89, 26–43, 1991.
Manning, L. A.: The Initial Radius of Meteoric Ionization Trails, J. Geophys. Res., 63, 181–196, https://doi.org/10.1029/JZ063i001p00181, 1958.
McKinley, D. W. R.: Meteor Science and Engineering, McGraw-Hill, New York, 1961.
Meek, C. E., Manson, A. H., Hocking, W. K., and Drummond, J. R.: Eureka, 80∘ N, SKiYMET meteor radar temperatures compared with Aura MLS values, Ann. Geophys., 31, 1267–1277, https://doi.org/10.5194/angeo-31-1267-2013, 2013.
Mertens, C. J., Mlynczak, M. G., López-Puertas, M., Wintersteiner, P. P., Picard, R. H., Winick, J. R., Gordley, L. L., and Russell III, J. M.: Retrieval of mesospheric and lower thermospheric kinetic temperature from measurements of CO2 15-mm Earth limb emission under non-LTE conditions, Geophys. Res. Lett., 28, 1391–1394, 2001.
Mertens, C. J., Schmidlin, F. J., Goldberg, R. A., Remsberg, E. E., Pesnell, W. D., Russell, J. M., Mlynczak, M. G., López-Puertas, M., Wintersteiner, P. P., Picard, R. H., Winick, J. R., and Gordley, L. L.: SABER observations of mesospheric temperatures and comparisons with falling sphere measurements taken during the 2002 summer MaCWAVE campaign, Geophys. Res. Lett., 31, L03105, https://doi.org/10.1029/2003GL018605, 2004.
NASA GES DISC: The Aura/MLS data, available at: http://disc.sci.gsfc.nasa.gov/Aura/data-holdings/MLS, last access: 12 May 2018.
Olsson-Steel, D. and Elford, W. G.: The true height distribution and flux of radar meteors, in: European Regional Astronomy Meeting of the IAU, 67, 193–197, 1987.
Pellinen-Wannberg, A. and Wannberg, G.: Meteor observations with the European Incoherent Scatter UHF Radar, J. Geophys. Res., 99, 11379–11390, https://doi.org/10.1029/94JA00274, 1994.
Rogers, L. A., Hill, K. A., and Hawkes, R. L.: Mass loss due to sputtering and thermal processes in meteoroid ablation, Plan. Space Sci., 53, 1341–1354, 2005.
SABER data services: The TIMED/SABER data, available at: http://saber.gats-inc.com/data.php, last access: 12 May 2018.
Singer, W., Latteck, R., Millan, L. F., Mitchell, N. J., and Fiedler, J.: Radar Backscatter from Underdense Meteors and Diffusion Rates, Earth, 102, 403–409, https://doi.org/10.1007/s11038-007-9220-0, 2008.
Steel, D. I. and Elford, W. G.: The Height Distribution of Radio Meteors – Comparison of Observations at Different Frequencies on the Basis of Standard Echo Theory, J. Atmos.-Terr. Phys., 53, 409–417, https://doi.org/10.1016/0021-9169(91)90035-6, 1991.
Thomas, R. M., Whitham, P. S., and Elford, W. G.: Response of high frequency radar to meteor backscatter, J. Atmos.-Terr. Phys., 50, 703–724, https://doi.org/10.1016/0021-9169(88)90034-7, 1998.
Tsutsumi, M., Tsuda, T., Nakamura, T., and Fukao, S.: Temperature fluctuations near the mesopause inferred from meteor observations with the middle and upper atmosphere radar, Radio Sci., 29, 599–610, https://doi.org/10.1029/93RS03590, 1994.
Westman, A., Wannberg, G., and Pellinen-Wannberg, A.: Meteor head echo altitude distributions and the height cutoff effect studied with the EISCAT HPLA UHF and VHF radars, Ann. Geophys., 22, 1575–1584, https://doi.org/10.5194/angeo-22-1575-2004, 2004.
Younger, J. P.: Theory and Applications of VHF Meteor Radar Observations, Ph.D. thesis, University of Adelaide, Australia, 2011.
Younger, J. P., Reid, I. M., Vincent, R. A., and Holdsworth, D. A.: Modeling and observing the effect of aerosols on meteor radar measurements of the atmosphere, Geophys. Res. Lett., 35, L15812, https://doi.org/10.1029/2008GL033763, 2008.