the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Multiscale variation model and activity level estimation algorithm of the Earth's magnetic field based on wavelet packets
Oksana V. Mandrikova
Igor S. Solovyev
Sergey Y. Khomutov
Vladimir V. Geppener
Dmitry M. Klionskiy
Mikhail I. Bogachev
We suggest a wavelet-based multiscale mathematical model of geomagnetic field variations. The model is particularly capable of reflecting the characteristic variation and local perturbations in the geomagnetic field during the periods of increased geomagnetic activity. Based on the model, we have designed numerical algorithms to identify the characteristic variation component as well as other components that represent different geomagnetic field activity. The substantial advantage of the designed algorithms is their fully automatic performance without any manual control. The algorithms are also suited for estimating and monitoring the activity level of the geomagnetic field at different magnetic observatories without any specific adjustment to their particular locations. The suggested approach has high temporal resolution reaching 1 min. This allows us to study the dynamics and spatiotemporal distribution of geomagnetic perturbations using data from ground-based observatories. Moreover, the suggested approach is particularly capable of discovering weak perturbations in the geomagnetic field, likely linked to the nonstationary impact of the solar wind plasma on the magnetosphere. The algorithms have been validated using the experimental data collected at the IKIR FEB RAS observatory network.
Keywords. Magnetospheric physics (storms and substorms)
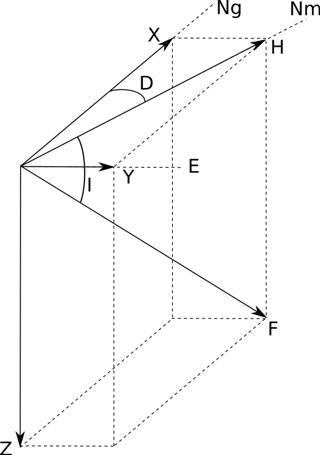
The Earth has its own magnetic field, which is also widely known as the geomagnetic field (also called “the Earth's geomagnetic field” or “the Earth's magnetic field”) (Bartels et al., 1939). The Earth's magnetic field varies continuously with both time and ambient space and can be represented as a superposition of the main field, the local field, and the variable field (Zaitsev et al., 2002). The above elements of the Earth's magnetic field are typically described using the rectangular coordinate system, where the axes are directed towards north, east, and downwards (Fig. 1).
The Earth's magnetic field vector can be represented either by components X, Y and Z in the Cartesian reference system with axes to geographical north, east, and vertically downwards, respectively, or by components H (horizontal), D (declination) and Z in the cylindrical system. Another alternative is using components F (total intensity), D and I (inclinations) in the spherical system. H points to magnetic north, D is the angle between the geographical and magnetic meridians and is positive to the east, while I is the angle between the horizontal component and the intensity vector.
As a rule, the horizontal component of the field (H component) is used for calculating the indices of geomagnetic activity (Menvielle et al., 1995; Nowożyński et al., 1991) and analyzing variations in the Earth's magnetic field during magnetic storms. The observed temporal variations in the Earth's magnetic field vector components are referred to here as the geomagnetic signals.
This paper is particularly focused on the development of analysis techniques for geomagnetic signal fluctuations characterizing the complex spatiotemporal structure and dynamics of the variable geomagnetic field. The variable part of the field is induced by the corpuscular flows of the magnetized plasma emanating from the Sun along with solar wind. Detailed characterization of the fluctuation phenomena in observational geomagnetic signals at multiple scales from global effects to local perturbations is essential for the understanding of the intensity, type, and development of a magnetic storm.
The complex structure of geomagnetic signals and an insufficient number of adequate mathematical models make these data difficult to analyze using manual techniques. Conventional approaches mainly employ basic time-series analysis models and methods that include various smoothing operations (smoothing and trend extraction, Chen, 2007; Joselyn, 1979; Rangarajan, 1989; Sucksdorff et al., 1991). Periodic changes and patterns in the data are typically analyzed using traditional Fourier techniques (Berryman, 1978; Golovkov et al., 1989). However, observational geomagnetic signals are often nonstationary and exhibit a heterogeneous multiscale structure (e.g., Consolini et al., 2013; Klausner et al., 2013). Therefore conventional analysis techniques (smoothing and trend extraction, Fourier techniques), while being able to provide a rather general picture, result in the smoothing of the local perturbations that often contain important information about geomagnetic field activity and are explicitly associated with the development of magnetic storms.
To overcome the above limitations, we suggest here a specialized nonlinear approach to the analysis of the geomagnetic signals that is based on the wavelet transform (Mallat, 1999; Holschneider, 1995). In this paper, we studied variations in the geomagnetic field and estimated their characteristics using the approach based on wavelet packets and first suggested in the papers from Mandrikova et al. (2012, 2013b). Nowadays wavelets and wavelet packets are among the most frequently applied mathematical tools in signal processing (e.g., Hafez et al., 2010; Jach et al., 2006). Regarding applications in geophysics and, in particular, the Earth's magnetic field studies, we would like to emphasize some of the most significant advantages of wavelet-based approaches (Jach et al., 2006; Kumar and Foufoula-Georgiou, 1997; Mandrikova et al., 2011; Nayar et al., 2006; Rotanova et al., 2006; Xu et al., 2008):
-
Wavelets and wavelet packets are capable of tracking the multicomponent structure of the observational geomagnetic data, considering that geomagnetic signals exhibit multiscale features. The local multiscale components are largely hindered by trends, thus altogether constituting a complex signal structure.
-
Unlike wavelets, wavelet packets are a more flexible signal processing tool. Wavelets work only with a low-frequency component at each decomposition level and leave a high-frequency one unchanged. In contrast, wavelet packets act to decompose both the high-frequency and the low-frequency components at each decomposition level, providing better resolution and finer splitting of the time–frequency domain.
-
Wavelets and wavelet packets provide fast computational techniques for finding wavelet coefficients. These techniques are very important for processing long and/or high-resolution data sets.
Currently, the wavelet transform is steadily becoming more and more popular in the area of geomagnetic data analysis. Wavelet applications focus on studying nonstationary processes in the magnetosphere preceding and accompanying magnetic storms (Balasis et al., 2006), analyzing the dynamics of geomagnetic activity and detecting singularities (Zaourar et al., 2013), removing noise (during data preprocessing) (Kumar and Foufoula-Georgiou, 1997), studying the dynamics of the processes in the magnetosphere–ionosphere system (Kovacs et al., 2001), extracting the periodic components caused by the Earth's rotation (Jach et al., 2006; Xu et al., 2008), extracting low-frequency signals in the external magnetic field and specifying models of the magnetic field (Kunagu et al., 2013), finding precursors of intense solar flares (Barkhatov et al., 2016), automatically detecting magnetic storm development (Hafez et al., 2010), studying properties and characteristics of the waves of ultra-low frequency (ULF) of the magnetosphere (Balasis et al., 2012, 2013, 2015), and studying characteristics of solar daily variations based on data from ground-based magnetic stations (Klausner et al., 2013), as well as several other issues. Additional applications of wavelets include the estimation of different geomagnetic activity indices such as the K index (Mandrikova et al., 2012, 2013b), Dst index and the wavelet-based index of storm activity “WISA” (Jach et al., 2006; Xu et al., 2008).
Recently, a multiscale analysis of geomagnetic data has been applied to reveal the anisotropic and nonintermittent character of geofields, helping to distinguish between their strong and wide-range variability (Lovejoy et al., 2001). Furthermore, nonlinear effects have been described in the framework of multifractal models with particular applications to multifractal and magnetization fields (Pecknold et al., 2001). Additional applications of multiscale analysis to the geomagnetic field include descriptions of its long-term horizontal intensity variation, which are capable of tracking its intermittency and representing a more complex nature of geomagnetic response to solar wind changes than previously thought (Consolini et al., 2013).
The model proposed here is based on multiscale wavelet analysis and allows us to study characteristic variations in the geomagnetic field and nonstationary short-term changes characterizing fast-flowing processes in the magnetosphere. We also discuss how this model can facilitate an in-depth analysis of geomagnetic field variations. Previously we have shown that the wavelet-based multiscale model allows us to automate the procedure of determining the “quietest” days for calculating the Sq variation and K index by using the Bartels technique (Bartels et al., 1939) and automatic extraction and estimation of perturbations in the geomagnetic field (Mandrikova et al., 2013a, 2014). In this paper, in order to perform a more detailed analysis of the geomagnetic data and study nonstationary short-term variations in the geomagnetic field, we suggest an enhanced version of this model. We discuss the potential area of application of the suggested model and some practical techniques based on this model. Using a prominent example of the analysis of geomagnetic data from a network of ground-based stations, we demonstrate the potential of the suggested approach for studying variations in the field and extracting subtle features during periods of increased geomagnetic activity.
The paper is organized as follows. In the “Data used in the study” section, we provide data used in the research and information about the observatories registering these data. The section also contains information on the analyzed magnetic storms. In the “Material and methods” section, we provide a brief theoretical outline of our wavelet-based approach, including the suggested multiscale model and associated algorithms to assess characteristic variations and local perturbations in the geomagnetic field during periods of increased geomagnetic activity. In the “Experimental results and discussion” section, we validate our model and algorithms using the observational data obtained at magnetic observatories of Institute of Cosmophysical Research and Radio Wave Propagation (IKIR) and Y. G. Shafer Institute of Cosmophysical Research and Aeronomy (IKFIA) of the Russian Academy of Sciences and Guam observatory (United States Geological Survey). In the “Conclusions” section, we have provided the main results of our research.
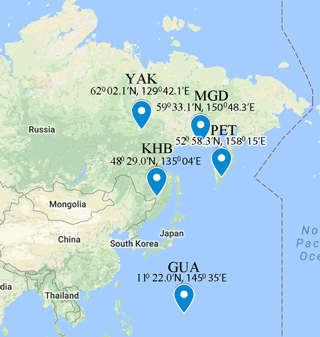
Experiments were carried out using the geomagnetic data (horizontal component of the magnetic field) obtained at the IKIR observatories Paratunka (PET), Magadan (MGD) and Khabarovsk (KHB) (in the eastern region of Russia). Additional data sets for the analysis were kindly offered by the Yakutsk (YAK) observatory of the IKFIA (Siberian region of Russia). Magnetic data from the Guam observatory were obtained from INTERMAGNET (GUA, http://www.intermagnet.org; last access: 30 August 2018) and used for the analysis of the equatorial magnetospheric processes. More detailed information on the geographical location of the observatories is represented inF Fig.1 and Table 1.
Table 1Observatories whose data were used.
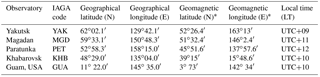
* Geomagnetic coordinates were calculated using the IGRF model (Thebault et al., 1964; http://wdc.kugi.kyoto-u.ac.jp/igrf/gggm/index.html; last access: 30 August 2018).
We use only magnetic data at minute-scale resolution obtained at observatories in accordance with INTERMAGNET Standards (http://intermagnet.org; last access: 30 August 2018), i.e., data that are free from noise, jumps, and long-term artificial and manmade effects and calculated by the standard Gaussian filtering of raw values.
Table 2The characteristics of the magnetic storms analyzed in the paper.
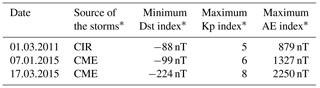
* Tables have been formed using the following data: The catalogue of ICMES by Ian Richardson and Hilary Cane, http://www.srl.caltech.edu/ACE/ASC/DATA/level3/icmetable2.htm (last access: 30 August 2018); Space Weather Prediction Center, ftp://ftp.ngdc.noaa.gov/STP/swpc_products/daily_reports (last access: 30 August 2018); International Service of Geomagnetic Indices (ISGI) http://isgi.unistra.fr (last access: 30 August 2018).
The results of our analysis were compared with data from the interplanetary magnetic field and the parameters of solar wind (http://www.srl.caltech.edu/ACE/ASC/index.html; last access: 30 August 2018). In order to analyze geomagnetic activity in the auroral zone, we used the index of an auroral electrojet (AE) (http://isgi.unistra.fr; last access: 30 August 2018). Calculation of the AE index is based on the data of stations located in auroral and subauroral latitudes (Davis and Sugiura, 1966). In order to analyze the equatorial current system, we used the Dst index (http://wdc.kugi.kyoto-u.ac.jp/dst_final/index.html; 30 August 2018), which is calculated using the data from the stations near the Equator (Sugiura, 1964). The characteristics of the analyzed magnetic storms are provided in Table 2.
3.1 Model of geomagnetic field variation
In the wavelet domain, the geomagnetic field variations can be represented as (Mandrikova et al., 2012, 2013b):
where
-
is the characteristic signal component that characterizes typical variations in the geomagnetic field;
-
is the perturbed component (here and in the following j∈I is denoted as jpert), which characterizes geomagnetic perturbations arising during the periods of increased geomagnetic activity (during the quiet periods ;
-
is the noise;
-
is the wavelet basis;
-
is the basis generated by a particular scaling function;
-
and dj,n are the coefficients calculated as and , where the symbol 〈…〉 implies the scalar product;
-
I is the index set for the perturbed components;
-
j is the scale;
-
m is the wavelet packet decomposition level;
-
n is the sample number.
3.2 Identification of the characteristic component of geomagnetic field variation
To estimate the characteristic component fchar(t) for a given f0(t) we introduce the operator D such that . This particular definition of D depends on the given a priori information. Since the a priori probability distribution is unknown, we consider its minimax estimate as recommended by Levin (1963) and Mallat (1999).
Then the purpose is to minimize the maximum risk for the set Θ with fchar. In order to control the risk we next calculate the maximum risk
where .
The minimal risk is the lower boundary calculated for all operators D:
and the task is to find the operator D satisfying Eq. (2).
The component reflecting the characteristic changes in diurnal variations in the Earth's magnetic field is called the quiet-day diurnal variation (Sq variation) (Bartels et al., 1939; Chen et al., 2007; Klausner et al., 2013; Mandrikova et al., 2012, 2013b). The Sq variation is characterized by the Sq curve, which is calculated as an average smoothed curve over several quiet diurnal variations in the geomagnetic field observed in the neighboring days (typically, variations over 3–5 days are averaged). This averaging is required because the Sq variation does not remain constant and its day-to-day reproducibility is quite limited. Since no functional description of the probability distribution of the Sq variation universal for all locations is available, it is advisable to use the minimax approach for finding the best solution (Levin, 1963; Mallat, 1999).
Wavelet packet transform will be employed as a solution operator. In this case the characteristic variation is introduced as the approximation component determined in the wavelet domain by the coefficients . We will take the Sq curve as a reference function for the error estimation since it reflects the quiet-day diurnal variation in the given geomagnetic signal (Bartels et al., 1939; Mandrikova et al., 2012, 2013b). The approximation error in the wavelet domain can be expressed as
where
-
is the coefficient vector of the approximating signal component;
-
is the coefficient vector of the approximating component of the Sq curve;
-
j is the scale;
-
m is the wavelet packet decomposition level;
-
n is the sample number;
-
T is the total number of samples per day.
According to Eq. (3) the estimation error depends on the decomposition level m and therefore there is an obvious need to find the decomposition level m∗, which provides the smallest approximation error for fchar(t).
Here we suggest a numerical stepwise algorithm for identifying the characteristic component of the geomagnetic signal model as outlined below.
-
The geomagnetic signal f0(t) is divided into segments of duration T, where T is equal to 1 day (N is the total number of discrete samples in the entire signal):
-
The Sq curve and each segment of the geomagnetic signal are transformed into the wavelet domain using wavelet packets. The wavelet-packet transform is performed for , where J is determined by the segment length T: J≤log 2T. Finally, we obtain the Sq curve components and each segment in the following form:
where l is the segment number.
-
The reconstruction of the components and is performed at each level m. Then the components are expressed as and , and is estimated by applying expression Eq. (3):
-
The decomposition level m∗, which provides the lowest risk, is calculated as
-
The characteristic component of the geomagnetic signal is finally expressed as
The resulting estimate can be improved by choosing the value for φ that provides the lowest approximation error.
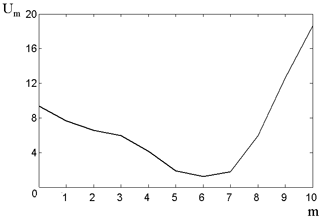
Using the data from the Paratunka observatory for 2002–2008 and the algorithm above (steps 1–5), we calculated the estimation error of the characteristic field variation for various wavelet bases and decomposition levels. The goal was to find the optimal scale m∗ that provided with the smallest approximation error for fchar(t) (see Eq. 3). Figure 3 shows the error of the characteristic variation estimation Um versus the decomposition level m. The figure indicates that for the chosen example, the smallest approximation error is obtained for the sixth decomposition level using the Daubechies wavelets (Daubechies, 2001) of the third order (see Fig. 3). Thus the reconstruction of the geomagnetic field variation component in the wavelet decomposition basis can be expressed as (see Eq. 1)
where are the approximating coefficients of the sixth decomposition level for the wavelet packet decomposition, is the basis function, and the component determines detailed coefficients containing perturbations. The index set I includes the second, fourth, fifth, and sixth scale levels.
3.3 Extraction of the perturbed components of geomagnetic field variation
The degree of the geomagnetic signal disturbance is the so-called perturbation magnitude (Bartels et al., 1939), which can be assessed by calculating the difference between the greatest and the smallest deviations of the current field variation from the characteristic diurnal variation, namely the Sq curve. In the suggested model (Eq. 1) the geomagnetic perturbations are characterized by the component
where , j∈I are denoted as jpert.
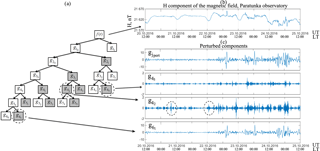
Figure 4Decomposition of the geomagnetic signal and its components in the period of a magnetic storm on 22–24 October 2016: (a) signal decomposition scheme, with perturbed components marked by the grey color; (b) H component of the Earth's magnetic field, Paratunka observatory; (c) perturbed components of the geomagnetic field variations.
In order to identify the perturbed component of the geomagnetic signal model, we next employ the wavelet-packet tree components , which characterize the respective perturbations. According to the results published earlier in Mandrikova et al. (2012, 2013b), the geomagnetic disturbance Aj of the wavelet-packet tree component can be determined as
Then the identification of these components is performed following Rule 1:
where is the sample average of the greatest wavelet coefficients (for scale j) for perturbed days, is the average of the greatest wavelet coefficients (for scale j) for quiet days, v is the index of the perturbed field variation, k is the index of the quiet field variation, and εj determines a systematic shift between the perturbed and the quiet days.
Assuming is normally distributed with mean and variance , it is possible to estimate εj as
where is the variance of the greatest wavelet coefficients (for scale j) for quiet days (this variance is determined as a result of multiple measurements); is the quantile of the standard normal distribution; nk is the number of analyzed quiet-field variations. For α=0.1 the confidence probability is , the quantile is , and .
The scales jpert are obtained from Eq. (7), correspond to the perturbed components of the model, and characterize the storminess of the magnetic field.
Figure 4 exemplifies the geomagnetic signal decomposition for the observatory PET (Kamchatka) data, including the results of the extraction of perturbed components of the field variation by applying Rule 1 for the perturbed period during 22–24 October 2016. All decompositions included here and below were performed based on a third-order Daubechies wavelet determined by minimizing the approximation error (Mandrikova et al., 2012, 2013b). Signal components with perturbations are shown in the diagram in grey (Fig. 4a). The analysis of the results in Fig. 4b confirms the complex and nonstationary structure of a geomagnetic signal, which includes multiscale components of the wide frequency band arising at random time points and characterizing periods of increased geomagnetic activity. One can see that, particularly prior to the magnetic storm, on 20–22 October the component already contains short-term (instantaneous) increases in the magnitude of the wavelet coefficients (Fig. 4c, indicated by dashed ellipses), which are possibly connected with instantaneous changes in the parameters of the interplanetary environment (currents at magnetopause) (Gonzalez et al., 1999; Yermolaev and Yermolaev, 2010; Zaitsev et al., 2002). During the event, geomagnetic perturbations exhibit a wider spectrum and the magnitude of the wavelet coefficients increases drastically. Remarkably, a considerable growth in the geomagnetic perturbations on 22–24 October could also be observed, especially during the evening and night (18:00–06:00 LT), which appeared to be more pronounced in the components and gpert (see Fig. 4c) and is probably associated with current intensification in the tail of the magnetosphere (Gonzalez et al., 1999; Yermolaev and Yermolaev, 2010; Zaitsev et al., 2002).
3.4 Determining the quietest days and calculation of the Sq variation
In order to determine the characteristic diurnal variation, one has to identify the quietest diurnal variations for the analyzed time period and then calculate the average smoothed curve by averaging the variations over these days (usually the 5 quietest diurnal field variations within a period of 1 month are considered). The resulting curve determines the quiet-day diurnal variation in the geomagnetic field.
Identification of the quietest diurnal variations can be performed automatically by another suggested Rule 2:
if
where L is the component length, then for the scale jpert is more perturbed than . Then characterizes the degree of disturbance of the signal component for the scale jpert.
Thus, by applying Rule 2 we can automatically detect the quietest diurnal variations in the magnetic field for the current month (normally the 5 quietest days are used) and then construct the average smoothed curve, namely the Sq curve, which is the zero baseline of the K index values (Bartels et al., 1939; Mandrikova et al., 2012, 2013b). Figure 5 indicates that by using Rule 2 the characteristic variations in the geomagnetic field and the quiet-day diurnal variations can be reconstructed using the suggested wavelet-based technique in a fully automatic mode. In contrast to the suggested approach, existing techniques do not allow for the automatic performance of this operation. At present, we have performed the software implementation of this technique for Kamchatka (PET, IKIR RAS) and Yakutsk (YAK, IKFIA SD RAS), and the results of K index during its online calculation are presented at http://www.ikir.ru/en/Data/datalfg.html (last access: 30 August 2018) and http://ysn.ru/intermagnet/kindex (last access: 30 August 2018).
3.5 Extraction of weak and strong perturbations in the geomagnetic field
Let us consider three possible geomagnetic field activity levels:
-
activity level h0 – the field is quiet (magnetic field is quiet);
-
activity level h1 – the field is weakly disturbed (magnetic field is weakly disturbed);
-
activity level h2 – the field is disturbed (magnetic field is disturbed).
According to these activity levels we can convert the mathematical model Eq. (1) to the following form:
where
-
fchar(t) is the characteristic component,
-
is the component characterizing weak geomagnetic perturbations,
-
is the component characterizing strong geomagnetic perturbations,
-
is the wavelet basis,
-
are the wavelet coefficients,
-
jpert is the scale,
-
n is the sample number,
-
I1,I2 are the index sets,
-
e(t) is the noise.
Consider the following conditions of for the introduced geomagnetic field activity levels:
-
– the coefficient is quiet;
-
– the coefficient is weakly disturbed;
-
– the coefficient is disturbed.
The degree of the magnetic disturbance is determined for its given magnitude by Eq. (6). To estimate and the threshold functions F1 and F2 are applied as follows:
The coefficients with the quiet condition are considered noise (they are equal to zero).
Both F1(x) and F2(x) determine the decision rules (Levin, 1963) for the condition of wavelet coefficients. Thresholds and split the coefficient space X into three nonintersecting areas: .
In our case the decision rule is deterministic: if the given data set falls in Xi, the hypothesis that a coefficient has condition is true. When a particular decision rule is used for the condition , the average losses are
where Πil is the loss function for erroneous decisions (each erroneous decision has its own cost), is the conditional probability of a data set falling in the area Xl, if condition has occurred and i≠l, i,l are the condition indices.
The conditional average of the losses for the given condition is known as the conditional risk. Averaging the conditional risk function for each of the conditions provides the average risk:
where pi is the a priori probability of the condition .
The value J∗ is the quality criterion for finding the decision rule. The best rule is the one providing the lowest average risk (known as the Bayesian risk; Levin, 1963).
Since the a priori distribution of the conditions is unavailable, we will use the a posteriori risk to obtain the best rule:
where the a posteriori probabilities provide the most complete characteristic of the conditions for the given observational data. For the simple loss function
the a posteriori risk Jl(x) equals
In this case the quality criterion for the decision rule is the smallest number of errors. The thresholds and are determined by the best decision rule, in particular the rule that provides the lowest value of Jl(x).
By minimizing Jl(x) we estimated the thresholds Tj,1 and for the region of Kamchatka. The estimates were based on the geomagnetic data from the Paratunka station for the period between 2002 and 2008. The disturbance degree of the geomagnetic field was characterized by the K index:
-
The coefficients belong to the area X0 (have the quiet condition , if the current value of the K index is equal to 0 or 1.
-
The coefficients belong to the area X1 (have the weakly perturbed condition , if the current value of the K index is equal to 2, 3 or 4.
-
The coefficients belong to the area X2 (have the perturbed condition , if the current value of the K index is greater than 4.
Application of operations (9) and (10) allows one to automatically extract weak and strong perturbations characterizing the activity level of the studied geomagnetic signal and thus to extract the information about the activity level of the geomagnetic field in the place of observation. The estimates have minute-scale time resolution, which allows one to obtain more detailed and prompt information about the activity of the geomagnetic field. It is also important that these transformations can be performed fully automatically.
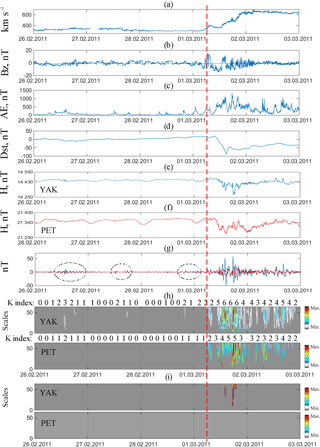
Figure 6Data processing results for the period from 26 February 2011 to 2 March 2011: (a) speed of solar wind (b) Bz component of the interplanetary magnetic field; (c) AE index; (d) Dst index; (e) magnetic field variation for the Paratunka observatory; (f) magnetic field variation for the Yakutsk observatory; (g) identified perturbed components of the field variations (blue line – Yakutsk observatory, red line – Paratunka observatory); (h) results of applying operation 9 (above the plots we can see K indices of the stations YAK and PET); (i) results of applying operation 10. The vertical dashed line indicates the onset of a magnetic storm.
Figure 6 presents the event on 1 March 2011 caused by the high-speed flow of solar wind from the coronal hole (Space Weather Prediction Center, ftp://ftp.ngdc.noaa.gov/STP/swpc_products/daily_reports). The figure exemplifies the results of extracting weak (operation 9, Fig. 6h) and strong (operation 10, Fig. 6i) geomagnetic perturbations. Figure 6 also shows perturbed components of the geomagnetic field variations extracted using Rule 1 (Fig. 6g).
Prior to a magnetic storm the speed of solar wind did not exceed 400 km s−1, Bz component of the interplanetary magnetic field (IMF) varied in the range of ±5 nT. The structure of the obtained data components (Fig. 6g) indicates some general regularity of the geomagnetic field variations at the analyzed stations YAK and PET. Prior to the event one can observe periods of moderate increase in the geomagnetic activity (indicates in Fig. 6g by the dashed ellipses), which correlate with the periods of moderate increase in the AE index (Fig. 6c, 26 February from 09:30 to 15:00 UT, 27 February from 12:15 to 13:20 UT, from 18:10 to 19:35 UT, 28 February from 19:30 to 20:25 UT; 1 March from 00:50 to 01:30 UT) that are probably connected with the field of the current system of polar perturbations. By applying threshold functions (operations 9 and 10, Fig. 6h, i) one can confirm the appearance of weak perturbations in the geomagnetic field prior to the event at the high-latitude YAK station, while at the PET station (midlatitude), the geomagnetic activity did not exceed the corresponding threshold (Eq. 9). The values of K indices at the PET and YAK stations (Fig. 6h) also confirm a moderate increase in the geomagnetic activity at high latitudes. Furthermore, at the beginning of the day on 1 March (from 05:00 UT) the speed of solar wind started increasing and the component IMFBz contained oscillations ±10 nT. Between 07:00 and 10:00 UT on 1 March the Dst index increased up to 20 nT, which confirms the outbreak of a magnetic storm (Gonzalez et al., 1999; Yermolaev and Yermolaev, 2010; Zaitsev et al., 2002). At the analyzed stations YAK and PET, one could observe weak perturbations (up to 10 nT, Fig. 6h). After 10:00 UT one could observe the onset of the main phase of a magnetic storm, which is characterized by a dramatic decrease in the Dst index (to −88 nT). During the main phase of the storm on 1 March from 09:10 to 15:45 UT, from 17:00 to 18:45 UT, from 19:45 to 20:45 UT one could see a dramatic rise of AE indices (to 1350 nT), which confirms strong substorms in the auroral area. An analysis of the perturbed components of the geomagnetic field variations (Fig. 6g) shows clear correlations between the periods of increase in AE indices and significant short-term increases in the geomagnetic activity at the YAK station (characterized by the abrupt peaks of high magnitude in the perturbed component) mostly during nighttime (from 21:00 to 06:00 LT) that could probably be associated with auroral processes and the intensification of currents in the magnetosphere's tail. The results of applying threshold functions (operation 10, Fig. 6i) confirm a significant increase in the activity at the YAK station during the main phase of the storm (1 March from 22:10 to 02:50 LT). At the midlatitude station PET, perturbations were rather moderate (did not exceed the thresholds , Fig. 6i) and exhibited activity on the low-frequency spectrum, which allows us to attribute them to the intensification of the ring current during the main phase of the storm (Gonzalez et al., 1999; Yermolaev and Yermolaev, 2010; Zaitsev et al., 2002). The recovery phase lasted for several days and was followed by continuous auroral activity (Fig. 6c) and weak perturbations in the field at the PET and YAK stations, which is typical (Gonzalez et al., 1999) of a storm caused by the high-speed flow of a coronal hole.
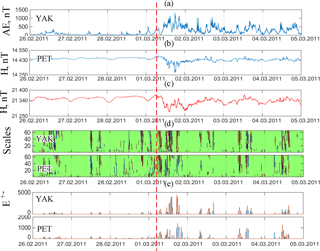
Figure 7Data processing results for the period from 26 February 2011 to 4 March 2011: (a) AE index; (b) magnetic field variation for the Paratunka observatory; (c) – magnetic field variation for the Yakutsk observatory; (d) results of applying adaptive thresholds Eq. (12), the red color indicates positive perturbations (increases relative to trend), the blue color shows negative ones (decreases relative to trend); (e) results of applying operation (13), the red color indicates positive perturbations (increases relative to trend), the blue color shows negative ones (decreases relative to trend). The vertical line indicates the onset of a magnetic storm.
3.6 Extraction and estimation of nonstationary short-term variations in the geomagnetic field
Due to the continuous variability of magnetospheric processes, especially during perturbed periods, we can introduce the adaptive thresholds and the coefficients , determining the component in Eq. (1):
where , , is the average value calculated in the gliding window of duration l, and U is the threshold coefficient.
Then following Eq. (6) the intensity of positive (I+) and negative (I−) perturbations in the geomagnetic field at the time point t=n can be determined as
Figure 7 shows the results of applying operations (12) and (13) with the following parameters: coefficient U=2 and window length l=720samples (corresponding to 12 h), Fig. 7d, e during the event on 1 March 2011 (the event is described above, see Fig. 6 and the description in Sect. 3.5). The analysis of the results in Fig. 7 confirms the efficacy of the adaptive thresholding Eq. (12) and shows that this allowed for the extraction of nonstationary short-term changes in data characterizing the appearance of weak increases in geomagnetic activity at the YAK and PET stations that preceded a major magnetic storm. The extracted perturbations could be observed nearly synchronously at the PET and YAK stations, correlated with the increase in the AE index, and were probably associated with short-term (instantaneous) changes in the parameters of the interplanetary environment (Gonzalez et al., 1999; Yermolaev and Yermolaev, 2010; Zaitsev et al., 2002). During the initial phase of the storm the intensity of the geomagnetic perturbations at the analyzed stations increased drastically (see Fig. 7e). During the main phase of the storm we also observed short-term dramatic increases in the intensity of the geomagnetic perturbations (see Fig. 7e). Thus, the application of Eqs. (12) and (13) allowed us to extract and estimate nonstationary (within the analyzed window of duration l) short-term increases in the geomagnetic activity, which provide a more in-depth view of the dynamics of geomagnetic processes.
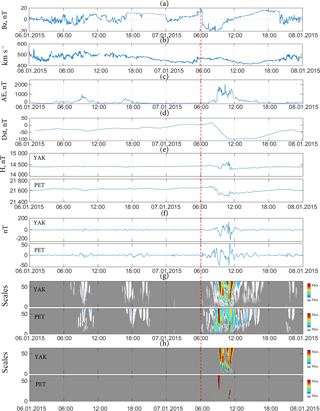
Figure 8Processing results of the data for 6–8 January 2015; (a) Bz component of the interplanetary magnetic field; (b) speed of solar wind; (c) AE index; (d) Dst index; (e) H component of the magnetic field; (f) identified perturbed components of the geomagnetic field variations; (g) results of applying threshold function (9); (h) results of applying threshold function (10). The vertical dashed line indicates the onset of a magnetic storm.
The suggested approach has been further validated for the events that occurred on 7 January 2015 and on 17 March 2015. These events have been studied by the authors in the works of Madrikova et al. (2017a, b). The results of corresponding tests are provided in Figs. 8–11. The first analyzed event, which happened on 7 January 2015 (see Figs. 8, 9), was associated with the coronal mass ejection (CME; the catalogue of ICMES by Ian Richardson and Hilary Cane, http://www.srl.caltech.edu/ACE/ASC/DATA/level3/icmetable2.htm) that occurred 3 days before exhibiting the typical phases of the Dst variation (Gonzalez et al., 1999; Yermolaev and Yermolaev, 2010; Zaitsev et al., 2002). Prior to the storm the speed of solar wind was greater than average (> 400 km s−1) (Gonzalez et al., 1999; Yermolaev and Yermolaev, 2010; Zaitsev et al., 2002) and the Bz component experienced a change of ±11 nT. Figure 8 shows that on 6 January, prior to the event, the increase on the AE index (Fig. 8c) at the analyzed stations was accompanied by weak perturbations in the geomagnetic field (see Fig. 8g, calculated by Eq. 9): at 07:00–11:00 UT, 16:00–18:30 and 19:20–21:10 UT at the YAK stations, at 8:00–11:00 and 17:00–21:10 UT at the PET stations. These results are in accordance with those of Davis (1997) and Zhang and Moldwin (2015), where prior to magnetic storms, one can observe characteristic increases in solar wind parameters and the power of IMF followed by increases in the geomagnetic activity indices (AE, Kp). The coincidence of the periods of increased geomagnetic activity at the analyzed stations with the periods in the AE index increases following fluctuations in the Bz component (Fig. 8a), allowing us to suggest the connection of the extracted geomagnetic perturbations with the nonstationary changes in the parameters of the interplanetary environment and the intensification of auroral activity (Gonzalez et al., 1999; Yermolaev and Yermolaev, 2010; Zaitsev et al., 2002). At the beginning of the day on 7 January, the Bz component turned to the south (at 00:20 UT) and in this period decreased to the value of −5 nT at both the YAK and PET stations. At the same time, short-term perturbations (from 01:15 to 01:30 UT, Fig. 8g) could be observed. Also, at the initial phase of the storm, increases in the Dst index (from 06:00 UT) and in auroral activity (see Fig. 8c) could be observed, accompanied by weak perturbations in the geomagnetic field at both the YAK and PET stations (Fig. 8g).
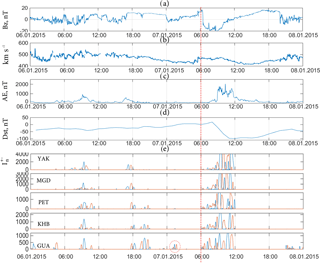
Figure 9Processing results of the data for 6–8 January 2015; (a) Bz component of the interplanetary magnetic field; (b) speed of solar wind; (c) AE index; (d) Dst index; (e) calculations following Eq. (13). Red color indicates positive perturbations (relative to trend), blue indicates negative (relative to trend). The vertical dashed line indicates the onset of a magnetic storm.
During the main phase of the storm the variations in the geomagnetic field at the analyzed stations exhibited a considerably different structure (see Fig. 8e, f) due to the location of these stations: YAK (52∘ of the geomagnetic latitude, 163∘ of the geomagnetic longitude) is located in the auroral area, while PET (45∘ of the geomagnetic latitude, 137∘ of the geomagnetic longitude) is located in the midlatitude area. Figure 8f, g, h show that the increase in the geomagnetic perturbations and the moments of extrema (where perturbations reached 175 nT at the YAK station while they reached 50 nT at the PET station) occurred at the stations at the same time, mostly during nighttime or evening hours.
An application of Eqs. (12) and (13) to the data from a network of meridionally located stations (from high latitudes to the Equator) shows the distribution of the perturbations along the meridian of observations and confirms the general dynamics of nonstationary short-term perturbations in the geomagnetic field prior to a magnetic storm and during the event (see Fig. 9e). Quantitative estimates (by Eq. 13, Fig. 9e) show significant correlations of the extracted geomagnetic perturbations with the AE index, not only in their occurrence times, but also in their intensities.
One can see that several hours prior to the onset of the magnetic storm (indicated by vertical dashed line in Figs. 8–11), weak variations in the interplanetary magnetic field (±5 nT), a moderate increase in the AE index (up to 150 nT), and a short-term moderate increase in the geomagnetic activity at the equatorial station GUA (shown in Fig. 9e by dashed circle: 7 January from 00:50 to 01:45 UT) were visible. This confirms the connection of the extracted perturbations with the auroral processes and also with the increase in the magnetosphere's tail currents during the main phase of a magnetic storm. Possible connections of the ring current with the processes in the auroral area are provided in Mendes et al. (2005). The reconstruction phase was short, at 20:00 UT the Dst index increased to −35 nT, which is common for the events from a CME (Gonzalez et al., 1999). At the end of the day on 7 January, fluctuations in the Bz component of the interplanetary magnetic field (±10 nT, Fig. 8a) accompanied by the fluctuations of the speed of solar wind (Fig. 8b) and followed by weak perturbations in the geomagnetic field at both YAK and PET stations (see Fig. 8g) as well as at the equatorial station GUA (see Fig. 9e) could be observed.
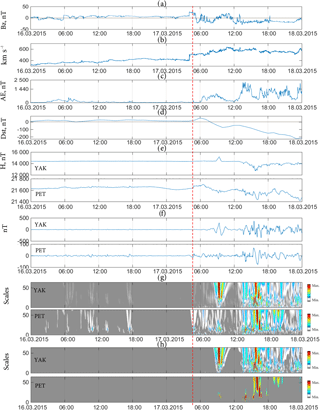
Figure 10Processing results for observations on 15–18 March 2015; (a) Bz component of the interplanetary magnetic field; (b) speed of solar wind; (c) AE index; (d) Dst index; (e) H component of the magnetic field; (f) identified perturbed components of the geomagnetic field variations; (g) results of applying the threshold function (9); (h) results of applying the threshold function (10). The vertical dashed line indicates the onset of a magnetic storm.
Figure 10 shows similar results obtained during the magnetic storm on 17 March 2015. This event is characterized as a “double storm” (magnetic storm with two main phases) and is caused by two separate emissions of the solar substance (the catalogue of ICMES by Ian Richardson and Hilary Cane, http://www.srl.caltech.edu/ACE/ASC/DATA/level3/icmetable2.htm). Prior to a magnetic storm the speed of solar wind gradually increased from 330 to 430 km s−1. Figures 10f–h and 11e, f show similar dynamics in the process preceding a storm. With fluctuations of the Bz component (±12 nT) and an increase in the AE index (up to 540 nT on 16 March from 02:50 to 10:00 UT), we can observe short-term weak geomagnetic perturbations at the analyzed stations. Synchronous perturbations at the analyzed stations (from those located at high latitudes to the Equator), their nonstationarity, and correlation with the AE index indicate a possible connection between the extracted perturbations and the variability of the interplanetary environmental parameters and an intensification of the auroral currents. Weak variations in the interplanetary magnetic field (±6 nT) accompanied by an increase in the AE index (up to 117 nT) and a short-term moderate increase in the geomagnetic activity at the equatorial station GUA (time period in Fig. 11f is indicated by the dashed line: 17 March from 00:00 to 03:10) several hours prior to the onset of the storm could be observed as well. The observed dynamics in interplanetary environmental parameters and geomagnetic activity variations is similar to the event considered above and accords with the results of Davis (1997) and Zhang and Moldwin (2015). At 04:00 UT on 17 March, due to the arrival of solar mass from CME (the catalogue of ICMES by Ian Richardson and Hilary Cane, http://www.srl.caltech.edu/ACE/ASC/DATA/level3/icmetable2.htm), the speed of solar wind reached 510 km s−1 while the Bz component of the interplanetary magnetic field reached 26 nT. In 45 min (at 04:00 UT) at the PET station, the onset of a magnetic storm was registered. At the YAK station the initial phase of the storm was less noticeable (Fig. 10e–g). The strongest geomagnetic perturbations at this station began occurring 08:50 UT (Fig. 10h), with their magnitude reaching 307 nT, (Fig. 10f). This was accompanied by the reduction in the Dst index in this period to −77 nT, and the AE index reaching 1055 nT.
Then the speed of solar wind reached 640 km s−1 and due to high-speed flows of solar mass from the second CME (reminiscent of the scenario considered in Gonzalez et al., 1999) beginning at 13:30 UT, one could observe the second main phase of the storm followed by strong perturbations in the geomagnetic field (at the YAK station the magnitude of perturbations reached 370 nT, while it reached 76 nT at the Paratunka station; see Fig. 10f, h, respectively) accompanied by a strong decrease in the Dst index (to −224 nT). During this period there were strong substorms in the auroral area, where the AE index reached a maximal value of −2250 nT (see Fig. 10c). A detailed analysis of the event based on the application of Eqs. (12) and (13) (see Fig. 11f) indicates that at the beginning of a magnetic storm, at all analyzed stations (from those located at high latitudes to the Equator), one could notice a short-term increase in the geomagnetic activity. During the fluctuations of the Bz component of the interplanetary magnetic field (to ±23 nT, Fig. 11a) and during an increase in the AE index (from 06:00 to 09:00 UT, Fig. 11c), strong short-term perturbations were observed, mostly at the stations closer to the north, particularly YAK, PET, and MGD (see Fig. 11f). After the arrival of high-speed flows of solar mass from the second CME on 17 March from 12:35 to 15:15 UT, one could observe a significant increase in the AE index (Fig. 11c), a decrease in the Dst index (Fig. 11d), and strong short-term perturbations in the geomagnetic field at all analyzed stations (Fig. 11f). An analysis of perturbed components of the field variations (Fig. 11e) and a comparison of the results with the results of Eqs. (12) and (13) (Fig. 11f) show that during the time of the greatest decrease in the Dst index (Fig. 11d) at low-latitude stations KHB and GUA, there were strong geomagnetic low-frequency spectrum perturbations (fluctuations with the period from 20 to 50 min, see Fig. 11e), which likely indicate their connection with the strong intensification of the ring current during the second main phase of a magnetic storm.
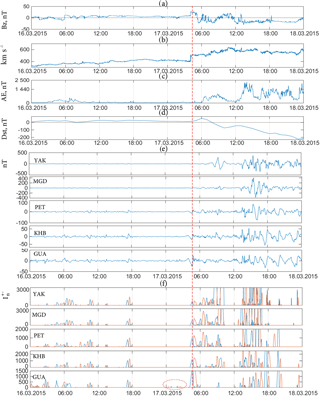
Figure 11Processing results for observations on 15–18 March 2015; (a) Bz component of the interplanetary magnetic field; (b) speed of solar wind; (c) AE index; (d) Dst index; (e) identified perturbed components of the field variations; (f) results of applying Eq. (13), red color indicates positive perturbations (increases relative to trend), blue indicates negative (decreases relative to trend). The vertical dashed line indicates the onset of a magnetic storm.
Our results indicate the complex dynamics of the spatiotemporal distribution of geomagnetic perturbations during the periods of increased solar activity and magnetic storms. A detailed analysis of the events on 7 January and 17 March 2015 confirmed the occurrence of weak short-term perturbations in the geomagnetic field prior to magnetic storms. The extracted perturbations were observed at all analyzed stations (from those located at high latitudes to the Equator), exhibited nonstationary behavior, and were accompanied by the fluctuations of the Bz component of the interplanetary magnetic field and increase in the AE index. These results are in accordance with those of Davis (1997) and Zhang and Moldwin (2015), which allows us to suggest their external nature and connection with the nonstationary impact of solar wind on the Earth's magnetosphere. In Davis (1997) and Zhang and Moldwin (2015), it has been shown that increases in solar wind parameters and the subsequent increases in geomagnetic activity (AE, Kp indices) can be observed prior to the abrupt turns of the IMF towards the south, then leading to magnetic storms (Lockwood, 2016).
The analysis of the results of this work also showed correlations of the occurring geomagnetic perturbations with the AE index not only in their occurrence times but also in their intensities. One possibility of extracting such abnormal effects as a result of processing ground-based geomagnetic data has also been suggested in Barkhatovetal (2016) and Sheiner and Fridman (2012) and was mentioned briefly in Mandrikova et al. (2013a). The analyses of the authors Barkhatov et al. (2016) and Sheiner and Fridman (2012), based on observational data and the joint analysis of the oscillations of the H component of the geomagnetic field with the oscillating processes on the Sun, have shown that the probability of these abnormal effects is high and reaches nearly 90 %. Here we have confirmed this effect using a very different approach and have shown explicitly that the suggested technique can successfully extract corresponding events. An analysis of the variations in the Dst index in the periods preceding magnetic storms can be found in Balasis et al. (2006), where we can also find the assumption that the critical feature of persistence in the magnetosphere is the result of combining solar wind with the internal magnetosphere activity (the magnetosphere is affected by solar wind).
Accordingly, an important aspect of this approach is the possibility of extracting prestorm anomalies based on the analysis of the ground-based data and the possibility of the automatic implementation of the technique, with online performance exhibiting only minor delays. Several hours prior to the analyzed magnetic storms, weak variations in the interplanetary magnetic field (±5 nT for 7 January and ±6 nT for 17 March) were accompanied by a moderate increase in the AE index (to 150 nT on 7 January and 117 nT on 17 March) and a moderate increase in the geomagnetic activity at the equatorial station GUA. During the main phases of the analyzed magnetic storms the geomagnetic perturbations increased drastically, exhibiting a nonstationary spectrum depending on the station where the data were measured, which could be attributed to the complex dynamics of the current system during magnetic storms (Gonzalez et al., 1999; Yermolaev and Yermolaev, 2010; Zaitsev et al., 2002).
To summarize, we have suggested, implemented, and validated a mathematical model and automated algorithms to analyze and describe the geomagnetic field variations based on the wavelet-based multiscale approach. Our results indicate that the model is particularly capable of reflecting the characteristic variation and local perturbations in the geomagnetic field during periods of increased geomagnetic activity. The efficiency of applying the wavelet transform in the analysis of geomagnetic data and the study of nonstationary processes in the magnetosphere can also be found in the works of other authors (e.g., Mendes et al., 2005; Hafez et al., 2013). In our research, we have suggested Rule 1 (operation 7) for identifying components containing geomagnetic perturbations. The magnitudes of the components extracted using Eq. (7) allow us to estimate the degree of geomagnetic activity.
In most cases when we need to extract nonstationary changes in the geomagnetic field we use the threshold (Balasis et al., 2013; Jach et al., 2006; Hafez et al., 2013; Mendes et al., 2005) together with the wavelet transform. In our work, we have suggested the technique of threshold estimation, and these thresholds allow us to extract geomagnetic perturbations in varying intensities (see Eqs. 9 and 10). We have also considered the adaptive threshold (see Eq. 12) for a more detailed analysis of the dynamics of the process. Analyses of moderate magnetic storms on 1 March 2011 and 7 January 2015 and of strong magnetic storms on 17 March 2015 have shown the efficiency of the suggested solutions.
Our experimental results clearly indicate the high sensitivity of the suggested technique and the possibility of its application in the in-depth study of the dynamics and spatiotemporal distribution of the geomagnetic perturbations (based on processing data from a network of geomagnetic observatories) for different levels of activity in the geomagnetic field. The suggested algorithms can be fully automated and allow one to find the moments of the increased geomagnetic activity and estimate quantitative characteristics of the degree of field perturbation. The suggested approach has high temporal resolution (up to 1 min), which helps us obtain detailed information on the activity level of the geomagnetic field in the case of nonstationary events. Moreover, the suggested approach is particularly capable of discovering weak perturbations that can occur prior to strong magnetic storms and could be associated with the nonstationary impact of the solar wind plasma on the magnetosphere.
Geomagnetic data from the stations of the Institute of Cosmophysical Research and Radio Wave Propagation are available at the following link: http://www.ikir.ru:8180 (Institute of Cosmophysical Research and Radio Wave Propagation FEB RAS, last access: 30 August 2018). Data from other stations are available to everyone (http://intermagnet.org; Intermagnet, last access: 30 August 2018). The algorithms used in the paper are provided in Sect. 3.4–3.6 and the values of the parameters of the threshold functions are given in Sect. 3.6.
OVM has developed the model and helped develop the algorithm, performed a detailed analysis of the processing results and prepared the manuscript. ISS has performed the estimation of model parameters, developed and implemented the algorithms, performed data processing and prepared the manuscript. SYK has performed primary data processing and helped analyze and edit the manuscript. VVG helped develop the model. DMK helped to analyze and edit the manuscript. MIB helped to analyze and edit the manuscript. All the authors took part in analyzing and discussing the results.
The authors declare that they have no conflict of interest.
The research is supported by the grant of the Russian Science Foundation
(project no. 14-11-00194). We would like to thank the staff of the geomagnetic
observatories at IKIR FEB RAS and at IKFIA SB RAS for providing high-quality
experimental data. The results presented in this paper rely on the data
collected at the Guam observatory. We thank USGS for supporting
its operation and INTERMAGNET for promoting high standards of magnetic
observatory practice (http://www.intermagnet.org; last
access: 30 August 2018).
The topical editor, Georgios Balasis,
thanks two anonymous referees for help in evaluating this paper.
Balasis, G., Daglis, I. A., Kapiris, P., Mandea, M., Vassiliadis, D., and Eftaxias, K.: From pre-storm activity to magnetic storms: a transition described in terms of fractal dynamics, Ann. Geophys., 24, 3557–3567, https://doi.org/10.5194/angeo-24-3557-2006, 2006.
Balasis, G., Daglis, I. A., Zesta, E., Papadimitriou, C., Georgiou, M., Haag-mans, R., and Tsinganos, K.: ULF wave activity during the 2003 Halloween superstorm: multipoint observations from CHAMP, Cluster and Geotail missions, Ann. Geophys., 30, 1751–1768, https://doi.org/10.5194/angeo-30-1751-2012, 2012.
Balasis, G., Daglis, I. A., Georgiou, M., Papadimitriou, C., and Haagmans, R.: Magnetospheric ULF wave studies in the frame of Swarm mission: a time-frequency analysis tool for automated detection of pulsations in magnetic and electric field observations, Earth Planet. Space, 65, 1385–1398, 2013.
Balasis, G., Papadimitriou, C., Daglis, I. A., and Pilipenko, V.: ULF wave power features in the topside ionosphere revealed by Swarm observations, Geophys. Res. Lett., 42, 6922–6930, https://doi.org/10.1002/2015GL065424, 2015.
Barkhatov, N. A., Obridko, V. N., Revunov, S. E., Snegirev, S. D., Shadrukov, D. V., and Sheiner, O. A.: Long-period geomagnetic pulsations as solar flare precursors, Geomagn. Aeron., 56, 265–272, 2016.
Bartels, J., Heck, N. H., and Johnson, H. F.: The three-hour-range index measuring geomagnetic activity, Terrestrial Magnetism and Atmospheric Electricity, 44, 411–454, 1939.
Berryman, J. G.: Choice of operator length for maximum entropy spectral analysis, Geophysics, 43, 1384–1391, 1978.
Chen, G. X., Xu, W. Y., Du, A. M., Wu, Y. Y., Chen, B., and Liu, X. C.: Statistical characteristics of the day-to-day variability in the geomagnetic Sq field, J. Geophys. Res., 112, https://doi.org/10.1029/2006JA012059, 2007.
Consolini, G., De Marco, R., and De Michelis, P.: Intermittency and multifractional Brownian character of geomagnetic time series, Nonlin. Proc. Geophys., 20, 455–466, 2013.
Daubechies, I.: Ten Lectures on Wavelets, Society for Industrial and Applied Mathematics, 2001.
Davis, C. J., Wild, M. N., Lockwood, M., and Tulunay, Y. K.: Ionospheric and geomagnetic responses to changes in IMF BZ: a superposed epoch study, Ann. Geophys., 15, 217–230, https://doi.org/10.1007/s00585-997-0217-9, 1997.
Davis, T. N. and Sugiura, M.: Auroral electrojet activity index AE, J. Geophys. Res., 71, 785–801, 1966
Golovkov, V. P., Papitashvili, V. O., and Papitashvili, N. E.: Automated calculation of the K indices using the method of natural orthogonal components, Geomagn. Aeron., 29, 667–670, 1989.
Gonzalez, W. D., Tsurutani, B. T., and Clua-Gonzalez, A. L.: Interplanetary origin of geomagnetic storms, Space Sci. Rev., 88, 529–562, 1999.
Hafez, A. G., Khan, T. A., and Kohda, T.: Clear P-wave arrival of weak events and automatic onset determination using wavelet filter banks, Digital Signal Processing, 20, 715–723, 2010.
Holschneider, M.: Wavelets: an Analysis Tool, Clarendon, Oxford, England, 1995.
Jach, A., Kokoszka, P., Sojka, J., and Zhu, L.: Wavelet-based index of magnetic storm activity, J. Geophys. Res., 111, a09215, https://doi.org/10.1029/2006ja011635, 2006.
Joselyn, J. A.: A real-time index of geomagnetic activity, J. Geophys. Res., 75, 2777–2780, 1970.
Klausner, V., Papa, A. R. R., Mendes, O., Domingues, M. O., and Frick, P.: Characteristics of solar diurnal variations: A case study based on records from the ground magnetic station at Vassouras, Brazil, J. Atmos. Sol.-Terr. Phys., 92, 124–136, 2013.
Kovacs, P., Carbone, V., and Vörös, Z.: Wavelet based filtering events from geomagnetic time-series, Planet. Space Sci., 49, 1219–1231, 2001.
Kumar, P. and Foufoula-Georgiou, E.: Wavelet analysis for geophysical applications, Rev. Geophys., 35, 385–412, 1997.
Kunagu, P., Balasis, G., Lesur, V., Chandrasekhar, E., and Papadimitriou, C.: Wavelet characterization of external magnetic sources as observed by CHAMP satellite: evidence for unmodeled signals in geomagnetic field models, Geophys. J. Int., 192, 946–950, https://doi.org/10.1093/gji/ggs093, 2013.
Levin, B. R.: Theoretical Basis of Statistical Radio Techniques, Fizmatgiz, Moscow, 1963.
Lockwood, M., Owens, M. J., Barnard, L. A., Bentley, S., Scott, C. J., and Watt, C. E.: On the origins and timescales of geoeffective IMF, Space Weather, 14, 406–432, https://doi.org/10.1002/2016SW001375, 2016.
Lovejoy, S., Pecknold, S., and Schertzer, D.: Stratified multifractal magnetization and surface geomagnetic fields – I. Spectral analysis and modeling, Geophys. J. Int., 145, 112–126, 2001.
Mandrikova, O. V., Solovjev, I. S., Geppener, V. V., and Klionskiy, D. M.: New wavelet-based approach intended for the analysis of subtle features of complex natural signals, S. Mach. Perc., 21, 293–296, 2011.
Mallat, S.: A Wavelet tour of signal processing, Academic Press, 1999.
Mandrikova, O. V., Smirnov, S. E., and Solov'ev, I. S.: Method for Determining the Geomagnetic Activity Index Based on Wavelet Packets, Geomagn. Aeron., 52, 111–120, 2012.
Mandrikova, O. V., Bogdanov, V. V., and Solovjev, I. S.: Wavelet Analysis of Geomagnetic Field Data, Geomagn. Aeron., 53, 268–276, 2013a.
Mandrikova, O. V., Solovjev, I., Geppener, V., Taha Al-Kasasbehd R., and Klionskiy, D.: Analysis of the Earth's magnetic field variations on the basis of a wavelet-based approach, Digital Signal Processing, 23, 329–339, 2013b.
Mandrikova, O. V., Solovev, I. S., and Zalyaev, T. L.: Methods of analysis of geomagnetic field variations and cosmic ray data, Earth Planet. Space, 66, https://doi.org/0.1186/s40623-015-0228-9, 2014.
Mendes, O. J., Oliveira, M. D., Mendes da Costa, A., and Clùa de Gonzalez, A. L.: Wavelet analysis applied to magnetograms: Singularity detections related to geomagnetic storms, J. Atmos. Sol.-Terr. Phys., 67, 1827–1836, 2005.
Menvielle, M., Papitashvili, N., Hakkinen, L., and Sucksdorff, C.: Computer production of K indices: review and comparison of methods, Geophys. J. Int., 123, 866–886, 1995.
Nayar, S. R. P., Radhika, V. N., and Seena, P. T.: Investigation of substorms during geomagnetic storms using wavelet Techniques, ILWS WORKSHOP, GOA, India, 9–24, 2006.
Nowożyński, K., Ernst, T., and Jankowski, J.: Adaptive smoothing method for computer derivation of K-indices, Geophys. J. Int., 104, 85–93, 1991.
Pecknold, S., Lovejoy, S., and Schertzer, D.: Stratified multifractal magnetization and surface geomagnetic fields – II. Multifractal analysis and simulations, Geophys. J. Int., 145, 127–144, 2001.
Rangarajan, G. K.: Indices of geomagnetic activity, in: Geomagnetism, edited by: Jacobs, J. A., vol. 3, Academic Press, London, 323–384, 1989.
Rotanova, N., Bondar, T., and Ivanov, V.: Wavelet Analysis of Secular Geomagnetic Variations, Geomagn. Aeron., 44, 252–258, 2004.
Sheiner, O. A. and Fridman, V. M.: The features of microwave solar radiation observed in the stage of formation and initial propagation of geoeffective coronal mass ejections, Radiophys. Quantum El., 54, 655–666, 2012.
Sucksdorff, C., Pirjola, R., and Häkkinen, L.: Computer production of K-values based on linear elimination, Geophys. Trans., 36, 333–345, 1991.
Sugiura, M.: Hourly values of equatorial Dst for the IGY, Ann. Int. Geophys. Year, 35, p. 44, 1964.
Thebault, E., Finlay, C. C., Beggan, C. D. et al.: International Geomagnetic Reference Field: the 12th generation, Earth Planet. Space, 35, 9–45, 1964.
Xu, Z., Zhu, L., Sojka, J., Kokoszka, P., and Jach, A.: An assessment study of the wavelet-based index of magnetic storm activity (WISA) and its comparison to the Dst index, J. Atmos. Sol.-Terr. Phys., 70, 1579–1588, 2008.
Yermolaev, Yu. I. and Yermolaev, M. Yu.: Solar and Interplanetary Sources of Geomagnetic Storms: Space Weather Aspects, Izv. Atmo. Ocean. Phy., 46, 799–819, https://doi.org/10.1134/S0001433810070017, 2010.
Zaitsev, A. N., Dalin, P. A., and Zastenker, G. N.: Sudden variations in the solar wind ion flux and their signature in the geomagnetic field disturbances, Geomagn. Aeron., 42, 717–724, 2002.
Zaourar, N., Hamoudi, M., Mandea, M., Balasis, G., and Holschneider, M.: Wavelet-Based Multiscale Analysis of Geomagnetic Disturbance, Earth Planet. Space, 65, 1525–1540, https://doi.org/10.5047/eps.2013.05.001, 2013.
Zhang, X. Y. and Moldwin, M. B.: Probabilistic forecasting analysis of geomagnetic indices for southward IMF events, Space Weather, 13, 130–140, https://doi.org/10.1002/2014SW001113, 2015.