the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Fast plasma sheet flows and X line motion in the Earth's magnetotail: results from a global hybrid-Vlasov simulation
Sanni Hoilijoki
Yann Pfau-Kempf
Urs Ganse
Riku Jarvinen
Markus Battarbee
Emilia Kilpua
Lucile Turc
Minna Palmroth
Fast plasma flows produced as outflow jets from reconnection sites or X lines are a key feature of the dynamics in the Earth's magnetosphere. We have used a polar plane simulation of the hybrid-Vlasov model Vlasiator, driven by steady southward interplanetary magnetic field and fast solar wind, to study fast plasma sheet ion flows and related magnetic field structures in the Earth's magnetotail. In the simulation, lobe reconnection starts to produce fast flows after the increasing pressure in the lobes has caused the plasma sheet to thin sufficiently. The characteristics of the earthward and tailward fast flows and embedded magnetic field structures produced by multi-point tail reconnection are in general agreement with spacecraft measurements reported in the literature. The structuring of the flows is caused by internal processes: interactions between major X points determine the earthward or tailward direction of the flow, while interactions between minor X points, associated with leading edges of magnetic islands carried by the flow, induce local minima and maxima in the flow speed. Earthward moving flows are stopped and diverted duskward in an oscillatory (bouncing) manner at the transition region between tail-like and dipolar magnetic fields. Increasing and decreasing dynamic pressure of the flows causes the transition region to shift earthward and tailward, respectively. The leading edge of the train of earthward flow bursts is associated with an earthward propagating dipolarization front, while the leading edge of the train of tailward flow bursts is associated with a tailward propagating plasmoid. The impact of the dipolarization front with the dipole field causes magnetic field variations in the Pi2 range. Major X points can move either earthward or tailward, although tailward motion is more common. They are generally not advected by the ambient flow. Instead, their velocity is better described by local parameters, such that an X point moves in the direction of increasing reconnection electric field strength. Our results indicate that ion kinetics might be sufficient to describe the behavior of plasma sheet bulk ion flows produced by tail reconnection in global near-Earth simulations.
Keywords. Magnetospheric physics (magnetospheric configuration and dynamics; plasma sheet) – space plasma physics (numerical simulation studies)
- Article
(8784 KB) -
Supplement
(33862 KB) - BibTeX
- EndNote
Earthward transport of energy, mass, and magnetic flux on the nightside of the Earth's magnetosphere occurs mainly through high-speed plasma flows, often in association with substorm activity (Baumjohann et al., 1989; Angelopoulos et al., 1994; Juusola et al., 2011b). Earthward flows are typically observed as localized (a few Earth radii wide channels), short-lived (∼10 min) events during which brief (∼ 1 min) high-speed (>400 km s−1) flow bursts alternate with near-stagnant plasma (Baumjohann et al., 1989, 1990). Such events are termed bursty bulk flows (BBFs; Angelopoulos et al., 1992). The processes leading to the structuring of the flows and their interaction with the ambient magnetosphere are not yet fully understood. The different timescales of the flow structuring may also have different origins, and, thus, different drivers. In particular, the roles of drivers external and internal to the magnetosphere are not well established, nor are the factors that determine the motion of the fast flow source regions, i.e., reconnection sites or X lines, clearly understood.
1.1 Occurrence of plasma sheet flows
Fast flows are most commonly observed when the interplanetary magnetic field (IMF) is southward and the solar wind speed high (Myllys et al., 2015). They originate as jets expelled by tail reconnection, the initiation of which is associated with the substorm onset. Reconnection starts after the current sheet has become thin enough (Snekvik et al., 2012). The onset location is typically between RE (Earth radius) (McPherron et al., 1973; Miyashita et al., 2009), but there are many examples of onsets occurring closer to the Earth, even at RE (e.g., Sergeev et al., 2012). Here x refers to the x coordinate of the Geocentric Solar Magnetospheric (GSM) coordinate system, with its x axis from the Earth to the Sun, y axis perpendicular to the plane containing the x axis and the Earth's magnetic dipole, and the z axis completing the right-handed set. After the onset of reconnection, the X line typically retreats tailward (Baker et al., 1996; Runov et al., 2003).
The bursty nature of plasma sheet flows gives strong evidence that the tail reconnection producing them is spatially variable and/or temporally intermittent. However, it is not clear at what timescales the burstiness of the reconnection would manifest, and whether it could explain both the 10 min timescales of the flow events as well as their internal structure.
Fast flows observed between and −9 RE are mainly directed earthward (Shiokawa et al., 1997). Earthward of RE the occurrence rate of BBFs decreases with decreasing distance from the Earth (Angelopoulos et al., 1994), as does the speed of the flows (Juusola et al., 2011a). Nonetheless, flows with speeds of ∼1000 km s−1 have been observed as close to the Earth as RE (Juusola et al., 2011a). The occurrence frequency and speed of the earthward flows is closely linked with the substorm phase (Juusola et al., 2011b). Flows with moderate speeds between 100 and 500 km s−1 become slightly more frequent toward the end of the substorm growth phase. At onset there is a sharp increase in the occurrence of such flows, and during the recovery phase a gradual decrease. The occurrence frequency of faster flows with speeds exceeding 500 km s−1, on the other hand, increases only gradually during the substorm expansion phase, and peaks at the end of the phase.
After expulsion from the reconnection site, the subsequent dynamics of the earthward flows are determined by the curvature part of the magnetic force that acts to accelerate the plasma, and the magnetic pressure gradient part of the force that, together with the thermal pressure gradient force, acts to decelerate them increasingly as they approach the inner magnetosphere. As a net effect, the flows are accelerated until approximately −14 RE, after which they are decelerated (Karlsson et al., 2015). Fast flows that reach the transition region between the tail-like and dipolar magnetic field are diverted dawnward and duskward and can rebound from the strong dipole field (Birn et al., 1999; Chen and Wolf, 1999; Ohtani et al., 2009; Panov et al., 2010; Birn et al., 2011; McPherron et al., 2011; Juusola et al., 2013; Nakamura et al., 2013).
As the earthward flows reach the inner magnetosphere, the closed magnetic flux carried by them is piled up against the dipole field. This large-scale dipolarization (increase in the magnetic field elevation angle) of the tail magnetic field starts between RE and expands tailward, azimuthally, and earthward (Baumjohann et al., 1999; Miyashita et al., 2009). The large-scale dipolarization is associated with the disruption of the cross-tail current, formation of the substorm current wedge (SCW) (McPherron et al., 1973; Shiokawa et al., 1998; Birn et al., 1999), dispersionless particle injections at the geostationary orbit, irregular ultra low frequency (ULF) range magnetic pulsations called Pi2 (T=40–150 s) (Saito, 1969), and auroral breakup. Auroral breakup, which typically consists of structuring and explosive brightening of the equatorward arc, followed by auroral expansion, has been mapped to the junction of the thin current sheet and the outer part of the dipole-like configuration around 8–10 RE distance from the Earth (e.g., Sergeev et al., 2012).
1.2 Transient magnetic field structures associated with plasma sheet flows
Regions of piled-up magnetic flux are observed in front of BBFs. The sharp (a few seconds) increase in the z component of the magnetic field (Bz) at the leading edge of the piled-up flux is called the dipolarization front (Angelopoulos et al., 1992; Nakamura et al., 2011; Runov et al., 2009). The sharp increase (on the order of 10 nT) is typically preceded by a small (on the order of a few nT) transient decrease in Bz, reaching in some cases negative values (Ohtani et al., 1992, 2004). While the dipolarization is associated with a decrease in plasma density, the precursor decrease in Bz is accompanied by a density increase (Ohtani et al., 2004), indicating compressed plasma in front of the flow burst.
Signatures corresponding to the dipolarization fronts preceding earthward flows have also been found for tailward flows, although the Bz signature naturally has an opposite polarity (Ohtani et al., 2004) and is associated with the substorm plasmoid (Ieda et al., 1998). The plasmoid refers to the portion of the plasma sheet located tailward of the dominant X line, which is released and carried downtail when the X line has eaten its way through the closed plasma sheet field lines and proceeds to reconnect open lobe field lines.
Magnetic flux ropes are embedded within both earthward and tailward directed high-speed plasma flow peaks (Slavin et al., 2003, 2005; Imber et al., 2011). Flux ropes are helical magnetic field structures formed between pairs of X lines (N+1 X lines produce N flux ropes). The flux rope axis is typically oriented in the dawn–dusk direction, and the strong core field along the axis is caused by the nonzero ambient By present in the plasma sheet. According to models based on ion tearing, one of the multiple X lines outpaces the others and eventually starts to reconnect lobe field lines (Schindler, 1974; Coroniti, 1980; Büchner et al., 1991). The Alfvén speed is much higher in the lobes than in the plasma sheet, and as a result the reconnection rate at the X line increases significantly at this point. Outflows from this dominant X line sweep all other X lines and flux ropes away, those located on the earthward side being carried earthward, and those located on the tailward side being carried tailward.
Satellites observe flux ropes being carried past them by the high-speed plasma flows as bipolar magnetic field signatures. Flux ropes are formed on average at RE (Imber et al., 2011) and they have been observed from RE to RE (Slavin et al., 2003; Ieda et al., 1998). Slavin et al. (2003) estimated an occurrence frequency of ∼ one flux rope per 5 h of central plasma sheet observing time. Flux ropes are typically encountered in series of two or more, separated by a few tens of seconds (Imber et al., 2011).
Superposed epoch analysis of 16 earthward moving “BBF-type” flux ropes by Slavin et al. (2003) yielded an asymmetric bipolar Bz variation from nT (leading peak) to 9 nT (trailing peak) coinciding with a peak of ∼2 nT and a peak of ∼8 nT. Slavin et al. (2003) attributed the asymmetry of the bipolar signature to pile-up of the magnetic flux in front of the fast flow. The duration of the bipolar signature was ∼28 s. Application of the constant-α flux rope model yielded a diameter of 1.4 RE. Earthward plasma flow started to increase quickly ∼40 s prior to the flux rope center and peaked at ∼600 km s−1 ∼40 s afterward. Ahead of the flux rope, where the flow speed was increasing, there was a density compression. A superposed epoch analysis of 31 tailward moving “plasmoid-type” flux ropes produced a nearly symmetric Bz variation from ∼3 nT (leading peak) to −3 nT (trailing peak) coincident on a peak of ∼4 nT. The duration of the bipolar signature was ∼32 s, indicating a diameter of 4.4 RE. Tailward flows began to increase quickly ∼40 s prior to the flux rope center and peaked at ∼500 km s−1. Ahead of the flux rope, where the flow speed was increasing, there was a modest density compression (Slavin et al., 2003). The differences between earthward and tailward moving signatures probably reflect the different downstream conditions: while the earthward flows need to proceed against the Earth's rigid magnetic field, the tailward flows meet no obstacles once reconnection has reached lobe field lines (Ohtani et al., 2004).
In analogy to obstacles moving in the plasma sheet, flux ropes cause transient bipolar perturbations on nearby lobe magnetic field lines. Examination of these remote signatures termed traveling compression regions (TCRs) (Slavin et al., 2005) has yielded further information on the underlying plasma sheet bulges. The majority (80 %) of the TCRs observed by Slavin et al. (2005) at RE were moving earthward and the rest tailward. The average speed, duration and width of both types of signatures were quite similar, ∼800 km s−1, ∼35 s, and 4.3 RE, respectively. Typical separation between individual TCRs observed during multiple TCR events was ∼100–150 s, but events with smaller separations comparable to TCR width also occurred.
The signatures of earthward moving dipolarization fronts and flux ropes and tailward moving plasmoid fronts and flux ropes resemble each other. Both fronts and flux ropes occur in the plasma sheet (unlike TCRs, which occur in the lobes). They are identified as asymmetric bipolar Bz signatures, located near the leading edges of flow bursts. Telling them apart may sometimes be difficult. The bipolar Bz signature of the dipolarization front should be more asymmetric than that of the flux rope. The leading Bz decrease may not reach negative values at all, and the trailing positive Bz would be clearly longer-lasting (on the order of minutes or even step-like). Dipolarization fronts also lack the strong By core field. Trains of several flux ropes can be observed during one BBF or its tailward equivalent (Imber et al., 2011), associated with the leading edges of the individual flow bursts that comprise the bursty bulk flow. Dipolarization fronts, on the other hand, are typically reported as isolated events, possibly associated with the leading edge of the entire BBF.
1.3 Interaction and motion of plasma sheet flow source regions
Flux ropes have been interpreted as strong evidence for multiple reconnection sites in the near tail (Slavin et al., 2003). Simultaneous occurrence of multiple reconnecting X lines in the tail leads to interaction between the X lines, such as collision of the counterstreaming reconnection jets from two X lines (Alexandrova et al., 2016). Interaction between the X lines affects the motion of both X lines and flux ropes. For numerical simulations of subsolar reconnection this has been shown by Hoilijoki et al. (2017). Both earthward and tailward moving X lines have been observed in the tail, although in most cases the X line retreats tailward (Eastwood et al., 2010). Alexandrova et al. (2015) examined the motion of X lines around RE. Of the 24 observed X lines, 10 were isolated and the rest were observed in multiples (i.e., several X lines were observed during one observation period). Apart from two multiple reconnection X lines, all X lines were moving tailward along the tail current sheet. The X line speeds were between 10 and 230 km s−1, with an average of 80 km s−1. Alexandrova et al. (2015) attributed the tailward motion of the X lines to the pressure gradient (Russell and McPherron, 1973), although they could not verify whether the observed pressure gradient was the dominant force near the X line. Neither could they determine whether the observed gradient was the global background gradient or a locally enhanced one. In analogy to magnetic flux pile-up against the dipole field, flux pile-up against a flux rope (Nakamura et al., 2010) could locally increase the magnetic pressure gradient. However, this would be expected to result in a strong asymmetry in the earthward and tailward outflow speeds (Oka et al., 2008), which was not observed by Alexandrova et al. (2015). A similar effect would be expected were the X line moved by the dynamic pressure of a reconnection jet from another X line. In any case, it is not obvious how a pressure gradient would affect the motion of an X line, which is not a physical object with a mass.
Murphy (2010) derived an expression for the rate of X line retreat (dxn∕dt) in the one-dimensional case (, symmetry about z=0) based on Faraday's law. The expression describes dxn∕dt in terms of local parameters evaluated at the X point:
Here, Ey is the out-of-plane electric field and Bz the component of the magnetic field normal to the direction of motion. In the assumed geometry, the X line then moves in the direction of increasing reconnection electric field strength. In the resistive magnetohydrodynamic (MHD) limit (i.e., specifying the out-of-plane electric field using the resistive MHD Ohm's law), the X line retreats due to either advection by the bulk plasma flow (Vx) or by diffusion of the normal component of the magnetic field:
where η is the resistivity (Murphy, 2010). In the ideal MHD limit, the magnetic field is frozen into the plasma, and the X line is purely advected by the bulk plasma flow. Murphy et al. (2015) extended the expression of X line motion to the three-dimensional case:
where the elements of the Jacobian matrix M are given by
1.4 Scope of the present study
In this study we analyze a two-dimensional (2-D) polar plane simulation produced using the global magnetospheric hybrid-Vlasov model Vlasiator1. The simulation is driven by steady solar wind, with conditions favorable for the production of fast plasma sheet flows: high solar wind speed and southward IMF. Using the same simulation, Hoilijoki et al. (2017) showed that steady solar wind conditions lead to variable dayside reconnection rates and varying X point (2-D version of an X line) locations at the magnetopause. The variations were caused by the combined effects of magnetosheath fluctuations and interactions between neighboring X points and passing magnetic islands (2-D versions of flux ropes where the intense core field is replaced by elevated plasma pressure). We will use the terms X point and O point to refer to X lines and centers of flux ropes in a 2-D case.
About half an hour after the start of the simulation, tail reconnection begins. The sequence of events leading to the reconnection onset was analyzed by Palmroth et al. (2017). They also showed that ion number density variations in the lobe plasma affect the speed of the resulting plasma sheet flows such that higher lobe density, being associated with lower Alfvén speed, produces slower outflows than lower lobe density. The density variations in the lobes are produced for example when 2-D magnetic islands, formed by subsolar reconnection, merge with the ambient magnetic field, releasing the high-density plasma carried in their core on the semi-open flux tubes.
Our aim is to further examine to what extent internal magnetospheric processes during steady southward IMF and fast solar wind driving can explain the complicated spatial and temporal structure of fast plasma sheet flows and embedded magnetic structures in the context of substorm-like magnetotail dynamics. The absence of external solar wind triggers in the simulation, such as pressure pulses and rotating IMF, allows isolation of the internal effects. While Palmroth et al. (2017) already showed how variations produced by subsolar reconnection modulate the flows, we concentrate on the effects of tail reconnection. The Vlasiator simulation results, including virtual spacecraft observations, are compared with the wealth of real spacecraft observations documented in the literature. This allows us to determine to what extent a self-consistent hybrid-Vlasov simulation with full ion kinetic physics can reproduce the measured features.
The structure of the paper is as follows: the Vlasiator model is described in Sect. 2 and the results presented in Sect. 3. Section 4 contains a discussion, including limitations of the simulation. Section 5 summarizes the conclusions.
We have used the hybrid-Vlasov model Vlasiator (Palmroth et al., 2013, 2015; von Alfthan et al., 2014). In Vlasiator, ions are modeled as six-dimensional (6-D) velocity distribution functions and electrons are neglected apart from their charge-neutralizing behavior. The ion distribution function is propagated in time according to Vlasov's equation. The set of equations is completed by Ampère's law, Faraday's law, and a generalized Ohm's law such that the electric field is given by
Here, V is the ion bulk velocity, B is the magnetic field, ρq is the ion charge density, is the current density, and H m−1 is the vacuum permeability. The second term on the right-hand side of the equation is the Hall term. Compared to resistive MHD, where the electric field is given by
where η is resistivity; including the Hall term produces higher reconnection rates (Birn et al., 2001). In Vlasiator, there is no artificially added or enhanced resistivity and reconnection is triggered by numerical diffusion. Any further terms of the generalized Ohm's law, except those included in Eq. (5), are considered negligible at the current spatial resolution of Vlasiator (300 km).
Thus, Vlasiator includes ion kinetics but not electron kinetics. It allows self-consistent global modeling of the near-Earth plasma environment, including multi-temperature non-Maxwellian ion populations that cannot be realistically described using MHD. Unlike particle-in-cell (PIC) approaches, modeling ions as velocity distribution functions produces solutions that are numerically noiseless.
So far, Vlasiator has been applied to study proton distributions in the Earth's foreshock and magnetosheath (Pokhotelov et al., 2013; Kempf et al., 2015), the ULF foreshock under radial IMF (Palmroth et al., 2015), mirror modes in the Earth's magnetosheath (Hoilijoki et al., 2016), and magnetopause reconnection (Hoilijoki et al., 2017). Pfau-Kempf et al. (2016) discovered transient, local ion foreshocks caused by dayside magnetopause reconnection, while Palmroth et al. (2017) examined the onset of tail reconnection. Hoilijoki et al. (2017) showed that there is good correlation between local reconnection rates in the simulation and an analytical model of local 2-D asymmetric reconnection.
All these studies were carried out using simulations that are two-dimensional (2-D) either in the polar x–z plane or in the equatorial x–y plane, with three-dimensional (3-D) velocity space and electric and magnetic fields. Spatially 3-D simulations will be run after adaptive mesh refinement has been implemented in Vlasiator.
We use the same polar plane simulation as Hoilijoki et al. (2017) and Palmroth et al. (2017). The simulation box extends from x=300 000 km or ∼47 RE (1 RE=6371 km) on the dayside to 000 km or RE on the nightside, with z extending to ±360 000 km or RE. The spatial resolution is 300 km or 0.047 RE. The inner boundary is at a distance of 30 000 km or ∼5 RE from the origin. The velocity space in each spatial grid cell covers ±4020 km s−1 in each direction with a resolution of 30 km s−1. The simulation is otherwise similar to that analyzed by Pfau-Kempf et al. (2016), except that their simulation box was smaller, covering ±47 RE in both the x and z directions. The geomagnetic field is modeled as a 2-D line dipole centered at the origin, aligned with the z axis, and scaled to match the geomagnetic dipole strength (Daldorff et al., 2014). Thus, the coordinate system is comparable to the GSM system.
The solar wind flows into the simulation box from its sunward wall, copy conditions are applied to the other outer walls, and periodic boundary conditions to the out-of-plane (±y) directions. The inner boundary enforces a static Maxwellian velocity distribution and perfect conductor field boundary conditions. The inflowing solar wind driving the simulation is steady throughout the run, with a Maxwellian distribution function, proton density of 1 cm−3, temperature of 0.5 MK, velocity of −750 km s−1 along the x axis, and magnetic field of −5 nT along the z axis (purely southward IMF). The simulation output (moments and fields) is saved every simulated 0.5 s.
In this section, we first give an overview of the onset of lobe reconnection in the simulation and then examine the global development of the simulated magnetotail plasma sheet ion bulk flows (Sect. 3.2) and the related changes in the tail magnetic field configuration (Sect. 3.3). The behavior of the magnetotail plasma sheet X and O points, i.e., reconnection sites and the centers of magnetic islands, including the motion of major X points, is the topic of Sect. 3.4. In the final Sect. 3.5, we place virtual satellites in the tail and compare their observations with the measurement results cited in the Introduction.
3.1 Onset of lobe reconnection and fast flows
As can be seen in Animation S1 in the Supplement, lobe reconnection in the simulation starts at RE approximately 27:00 min (1620.0 s) after the beginning of the simulation. Figure 1 shows a snapshot from the animation at this moment. The plot shows proton β⟂ (ratio of thermal pressure perpendicular to the magnetic field and magnetic pressure) and magnetic field lines in the x–z plane. Closed field lines are drawn in green, open field lines in black, and IMF field lines in gray. Field lines that are closed but not attached to the geomagnetic field are drawn in magenta.
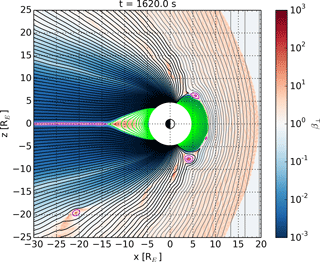
Figure 1Snapshot from Animation S1 in the Supplement at 1620.0 s (27:00). S1 illustrates the development of proton β⟂ (ratio of thermal pressure perpendicular to the magnetic field and magnetic pressure) and magnetic field lines in the x–z plane at 5 s resolution (reduced from 0.5 s due to file size limitations) between 1400.0 s (23:20) and 2150.0 s (35:50). Closed field lines are drawn in green, open field lines in black, and IMF field lines in gray. Field lines that are closed but not attached to the geomagnetic field are drawn in magenta.
Figure 2 shows the sum of magnetic pressure and thermal ion pressure perpendicular to the magnetic field at RE and y=0 (slightly earthward of the onset location) as a function of z and time (MM:SS). The onset times of lobe reconnection at 27:00 and fast flows at 28:00 (Sect. 3.2) are indicated by the black vertical lines. The yellow curves show the boundaries of the plasma sheet, identified as the region near the equatorial plane where plasma . Magenta crosses and green circles show the locations of X and O points, respectively, identified as local saddle points and extrema of the magnetic flux function (Yeates and Hornig, 2011; Hoilijoki et al., 2017). In addition to the plasma sheet X and O points around z=0, some X and O points are also visible in the magnetosheath. These correspond to tailward propagating 2-D magnetic islands, produced by subsolar reconnection (Pfau-Kempf et al., 2016; Hoilijoki et al., 2017), that are in the process of merging with the ambient magnetic field. Flux transfer event flux ropes formed on the dayside magnetopause have been observed to travel along the magnetopause in the anti-sunward direction and survive far ( RE) to the distant tail magnetopause (Eastwood et al., 2012). Animation S1 in the Supplement shows that in the simulation, the largest magnetic islands formed on the dayside magnetopause can get past the cusp and continue traveling tailward. The majority of the magnetic islands are dissipated in the cusp or very soon after it, through reconnection with the ambient magnetic field. This is in agreement with the simulation results of Omidi and Sibeck (2007) and Chen et al. (2017). The increased dynamic pressure of the magnetic islands compared to the surrounding magnetosheath plasma drives fast magnetosonic wave fronts ahead of the islands (Pfau-Kempf et al., 2016). These wave fronts are visible in Fig. 2 (the signature of the wave front always appears first near the plasma sheet due to the curvature of the wave front).
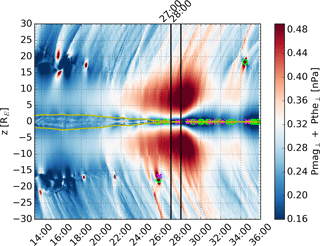
Figure 2Sum of magnetic pressure and thermal ion pressure perpendicular to the magnetic field at RE and y=0 as a function of z and time in minutes after the beginning of the simulation (MM:SS). The approximate onset times of lobe reconnection at 27:00 and fast flows at 28:00 are indicated by the black vertical lines. The yellow curves show the boundaries of the plasma sheet, identified as the region near the equatorial plane where plasma . Magenta crosses and green circles show the locations of X and O points, respectively.
Figure 2 illustrates how pressure in the lobes increases before reconnection starts in the tail current sheet. This increase is not smooth but occurs in steps, as the tailward propagating magnetic islands or their residuals compress the tail. Reconnection starts once the increase in lobe pressure has caused the plasma sheet to thin sufficiently (Snekvik et al., 2012). In the case of Vlasiator, this means the width of the spatial grid cell, as is typical for reconnection in numerical simulations in general. The location RE shown in Fig. 2 is slightly earthward of the actual onset location, and the earthward propagating X point is visible in the plot just before 28:00.
Palmroth et al. (2017) showed that while the preceding earthward propagating X–O pairs, visible in Fig. 2 between 25:00 and 27:00, were destroyed by merging with the dipole field, the X point visible just before 28:00 survived. The reason given was that because reconnection at the X point had reached lobe field lines, the outflows were strong enough to divert the direction of motion of the trailing O point, thus preventing it from merging with the dipole field and destroying the X point in the process (this can also be seen in Fig. 3 in the next section). Reconnection at the X point is at first relatively weak, and the lobe pressure keeps increasing after 27:00. As shown in the next section, the X point starts to produce fast plasma flows at 28:00. At this point, lobe pressure close to the plasma sheet starts to relieve.
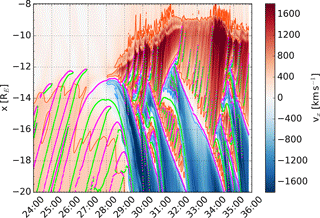
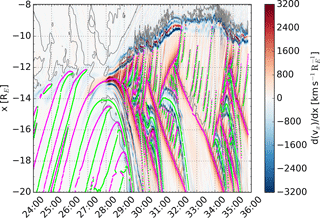
Figure 3Earthward component of the bulk ion velocity (Vx, color) in the magnetotail plasma sheet () as a function of x and time in minutes after the beginning of the simulation (MM:SS). The ±400 km s−1 contours are indicated with the orange and blue curves. Magenta and green dots show the locations of the X and O points, respectively.
3.2 Earthward and tailward bulk ion flows
Figure 3 shows the earthward component of the bulk ion velocity (Vx, color) in the magnetotail plasma sheet () as a function of x and time. The ±400 km s−1 contours are indicated with the orange and blue curves. Magenta and green dots show the locations of the X and O points, respectively. Near-Earth reconnection starts to produce fast earthward and tailward flows near RE about 28 min after the beginning of the simulation, roughly 1 min after the start of lobe reconnection. The simulation ends at 36:00, 8 min after the start of the fast flows. Thus, instead of the 10 min timescale variations related to BBFs we will concentrate on shorter variations related to plasma sheet flows, i.e., the internal structure of a BBF.
BBFs are typically identified from the bulk ion velocity perpendicular to the magnetic field, but we show the total bulk ion velocity. In Vlasiator the plasma sheet is thin (Fig. 2), and a small offset of the plasma sheet away from the z=0 plane can result in a lobe-like magnetic field configuration at z=0, with a relatively strong Bx and weak Bz. This will then result in a strong field-aligned and almost zero perpendicular plasma flow. Thus, showing the total bulk ion velocity gives a better description of the behavior of the flows. In Figs. 11 and 12 the perpendicular and parallel components are shown as well, for reference.
Figure 3 shows that between the start of the fast flows and the end of the simulation, all flows between and −8 RE are directed earthward. Earthward flows can also be found at all distances between and −20 RE, but their occurrence frequency decreases with increasing distance from the Earth such that at RE practically all flows are tailward. The simulation results in Fig. 3 can at certain times be interpreted in terms of a single dominant X point with earthward fast flows on the earthward side and tailward fast flows on the tailward side (e.g., 32:00–34:00), and at certain times in terms of two dominant X points with a stagnation region where the tailward flows from the earthward X point collide with the earthward flows from the tailward X point (e.g., 31:00–32:00). The results also show that more than two dominant X points can exist (e.g., ∼29:50), but such configurations are not as long-lived as those with only one or two dominant X points. The connection between X point properties and which points become dominant is not considered in the present study.
The speed of both earthward and tailward flows increases away from the X point because of magnetic tension. When the earthward flows reach the dipole field, they are abruptly decelerated. The deceleration is further illustrated by Fig. 4, which shows the derivative of Vx with respect to x. The gray curves are countours of zero total pressure in the x direction (). The flows are stopped when the combined magnetic and thermal pressure of the inner magnetosphere exceeds the dynamic pressure of the flows. The deceleration is not smooth, but occurs in an oscillatory manner, launching disturbances into the inner magnetosphere. Flow bursts with especially high speed and, consequently, high dynamic pressure, penetrate closer to the Earth than the surrounding flows. Such high-speed spikes can be seen for example around 30:00. In addition to being decelerated, the flows are also diverted toward dusk (preferred direction for ions in the near-Earth region) along the dipole field boundary. This is illustrated by Fig. 5, which shows the dusk component of the ion bulk velocity. In order to help comparison of the two plots, the orange and blue curves from Fig. 3 (±400 km s−1 contours of Vx as a proxy for the occurrence of fast flows) are shown as well. Duskward diversion of the earthward velocity also occurs in regions where faster flows overtake slower flows in front of them (e.g., between and −12 RE at ∼34:00). All these features are in accordance with the measurements cited in the Introduction.
3.3 Magnetic field configuration
Figure 6 shows the z component of the magnetic field. The ±400 km s−1 contours of Vx as orange and blue curves from Fig. 3 have again been overlaid to guide the eye. In addition to the bipolar signature of the magnetic islands, the thin positive stripes of newly closed magnetic flux carried by the earthward flows, and the newly detached (negative) magnetic flux carried by the tailward flows, it illustrates the behavior of the dipole field in response to the flows. Before the onset of the actual fast flows at ∼28:00, slower earthward flows in front of earthward moving X points (Palmroth et al., 2017) carry dipole flux toward the inner magnetosphere, resulting in a sharper boundary around RE with a stretched tail-like magnetic field configuration on the tailward side and a compressed dipole on the earthward side. This development is significantly enhanced at the onset of the fast flows, such that the stopping region of the fast flows moves earthward from RE to RE in ∼3 min. The stopping region then remains semi-stationary at RE until 34:00, after which it moves slightly tailward again. At the onset of the fast flows, a plasmoid is also detached, visible as the dark blue tailward moving signature between 27:00 and 30:00. Tailward moving bipolar signatures related to large magnetic islands can be seen approximately at 30:00–31:00, 31:00–32:30, 34:00–34:40, and 34:30–35:30.
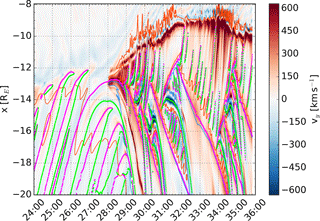
Figure 5Duskward component (Vy, color) in the magnetotail plasma sheet () as a function of x and time in minutes after the beginning of the simulation (MM:SS). The ±400 km s−1 contours are indicated with the orange and blue curves. Magenta and green dots show the locations of the X and O points, respectively.
We do not observe clear signatures of outward propagation of the dipole boundary due to flux pile-up (Baumjohann et al., 1999; Miyashita et al., 2009). According to Miyashita et al. (2009), ∼8 min after the onset of tail reconnection (which occurs ∼2 min before auroral substorm onset), dipolarization should have spread from RE to RE, corresponding to a tailward expansion speed of ∼100 km s−1. What we do observe, however, is that before the start of reconnection around 27:00, Bz is very weak tailward of the onset location at RE. After the onset, Bz is more strongly positive in regions located tailward of the dipole boundary (which has moved earthward) and earthward of major X points. As an X point retreats tailward, this region of more dipolar field expands tailward. The difference in amplitude is not large compared to the pre-onset time, but comparable to the 2 nT scale shown by Miyashita et al. (2009).
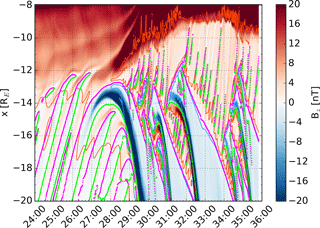
Figure 6The color shows the z component of the magnetic field as a function of x and time in minutes after the beginning of the simulation (MM:SS). The color scale has been saturated to better show plasma sheet structures that are weaker than the dipole field. Magenta and green dots show the locations of the X and O points, respectively. The ±400 km s−1 contours are indicated with the orange and blue curves.
As shown in more detail in Sect. 3.5.1 below, the leading edge of the earthward moving Bz enhancement that starts approximately around RE at 28:00 resembles dipolarization fronts observed by satellites. Runov et al. (2009) showed a case where the five THEMIS probes observed such a dipolarization front propagating earthward from to −11 RE at a constant speed of 300 km s−1. Our signature originates closer to the Earth, but according to Fig. 6 the dipolarization front appears to have a fairly constant speed on the order of 200 km s−1 (2 RE in 1 min). Runov et al. (2009) showed a transient dipolarization signature tailward of −11 RE, but at the most earthward probe around RE, the front was followed by a permanent increase in the Bz level, which might be associated with large-scale dipolarization.
Figure 7 is the same as Fig. 6 except that only variations in the Pi2 window (T=40–150 s; Saito, 1969) are shown. In order to obtain the plot, a Fourier transform of the time series of Bz at each x location was carried out using a box filter in the Pi2 window, and then an inverse transform was performed. The resulting plot illustrates that in the simulation, the dipolarization front launches a strong disturbance in the Pi2 window, as would be expected around substorm onset.
3.4 Reconnection sites and magnetic islands
Multiple X line reconnection produces N magnetic islands between N+1 reconnection sites (see, e.g., the illustration in Imber et al., 2011). New X and O points, i.e., reconnection sites and the centers of magnetic islands, emerge in pairs in Figs. 3–7. As can be seen in Fig. 6, an O point coincides with the center of a bipolar Bz signature, which has a negative Bz peak on the earthward side and a positive peak on the tailward side. On closed magnetic field lines, the ambient Bz is positive, and, thus, on the earthward side of the magnetic island there is a location where Bz=0. This coincides with an X point. On newly detached magnetic field lines, on the other hand, the ambient Bz is negative, and consequently, the corresponding X line is located on the tailward side of the magnetic island (e.g., RE at ∼35:30).
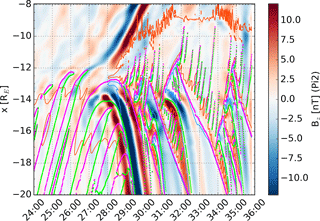
Figure 7The color shows variations in the Pi2 window (T=40–150 s) of the z component of the magnetic field as a function of x and time in minutes after the beginning of the simulation (MM:SS). Magenta and green dots show the locations of the X and O points, respectively. The ±400 km s−1 contours are indicated with the orange and blue curves.
There are four types of tail X–O pairs in the simulation: (1) earthward moving pairs that stay in close proximity to each other all their life, (2) tailward moving pairs that stay in close proximity to each other all their life, (3) pairs that emerge as earthward moving, get separated, and eventually, but still separately, end up moving tailward, and (4) newly formed pairs where a tailward moving O point separated from its original X point overtakes another separated X point tailward of it and they pair up. Thus, while X points can exist without an associated O point, O points always have an associated X point. When reconnection at a new X point reaches the lobe field lines, the magnetic island grows rapidly and the O point starts to separate from its earthward X point. We will call the single X points major X points and the X points associated with an O point minor X points. It should be noted that such a categorization only gives at most one major X point for each moment of time. Thus, some samples labeled “minor X points” may actually be major X points, i.e., X points where reconnection has reached lobe field lines. However, this simple categorization is enough for our purposes, as all samples labeled “major X points” should be correctly labeled, as should be the majority of the samples labeled “minor X points”.
In Fig. 6, new X–O pairs frequently emerge in the wake of retreating major X points (e.g., RE around 31:30, RE around 33:00), but rarely in front of them (e.g., RE around 31:30, RE around 33:00). Most likely this is related to the more favorable magnetic field configuration for reconnection behind a moving major X point than in front of one.
The X–O pairs are destroyed by merging with the dipole (e.g., RE at ∼30:00), a semi-stagnant magnetic island (e.g., RE at ∼31:30) or just the weak ambient field (e.g., RE at ∼33:00). The closest to the Earth that any X–O pairs reach in this simulation is RE just after 32:00 and before 34:00. The largest magnetic islands develop between two major X points (Fig. 6), where they gain magnetic flux and are compressed by the oppositely directed outflows from the X points.
Figure 8 displays the velocity of O points, minor X points, and major X points as a function of x. X/O point velocity at a given time t is calculated as . The X and O points existing before the onset of lobe reconnection have not been included in the analysis. There is a clear dependence of the velocity on x such that closer to the Earth the minor X points and O points tend to move earthward with higher speeds, and farther away from the Earth they tend to move tailward with higher tailward speeds. The behavior resembles closely that of the ion flows. Major X points, however, do not seem to follow this trend. As can be seen in Fig. 8, major X points typically end up retreating tailward at a fairly constant speed. The speeds of earthward moving major X points are highly scattered. The median values of positive and negative velocities are indicated in Fig. 8 by the dashed horizontal lines. The values −350 km s−1 (standard deviation ±315 km s−1) and 330 km s−1 (standard deviation ±190 km s−1) are somewhat faster than the 80 km s−1 average speed observed by Alexandrova et al. (2015).
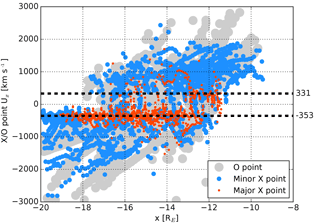
Figure 8Earthward velocity of magnetotail plasma sheet O points, minor X points, and major X points as a function of x. The median values of positive and negative major X point velocities are indicated by the dashed horizontal lines.
Figure 9 shows the earthward velocity of O points, minor X points, and major X points as a function of ion velocity Vx estimated at the locations of the X and O points. The line of equality is shown in solid black and linear fits to the O point values, minor X point values, and major X point values in dashed gray, blue, and red, respectively. In order to provide a measure for how well the ion bulk flow (Vx) can describe the X/O point velocity (Ux), the coefficients are indicated in the legend. The figure shows that while the speeds of the O points and minor X points are indeed more or less correlated with the ion flow speed, the speed of major X points is not.
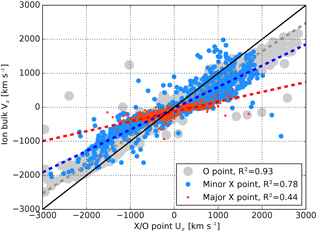
Figure 9Earthward velocity of magnetotail plasma sheet O points, minor X points, and major X points as a function of ion Vx estimated at the locations of the X and O points. The line of equality is shown in solid black and linear fits to the O point values, minor X point values, and major X point values in dashed gray, blue, and red, respectively.
In order to find out what determines the X point motion, Fig. 10 shows the x component of the expression of Eq. (3) (Murphy et al., 2015), estimated at the locations of the X points, as a function of X point velocity. We have adjusted Eq. (3) to the two-dimensional case, since in the polar plane simulation run . The O points are shown as well, for reference. There seems to be a correspondence between dxn∕dt estimated in terms of local parameters at the X point and the actual X point velocity. Comparison with Fig. 9 reveals that dxn∕dt describes X point motion, especially that of major X points, better than bulk ion Vx. For O points, on the other hand, correlations with Vx and dxn∕dt are very similar.
We tested the one-dimensional Eq. (1) as well, and it gave almost identical results, indicating there is no significant up–down asymmetry. The discrepancies in Fig. 10 are most likely caused by numerical errors, especially when estimating the derivatives (e.g., ). Furthermore, the method used to identify the X and O points does not necessarily place them at the simulation grid points and the parameters used to evaluate Eq. (3) are then obtained with respect to the nearest grid point.
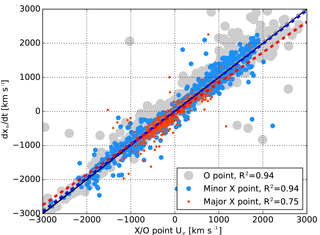
Figure 10The expression of Eq. (3) estimated at the locations of the magnetotail plasma sheet X and O points as a function of X point velocity. The line of equality is shown in solid black and linear fits to the O point values, minor X point values, and major X point values in dashed gray, blue, and red, respectively.
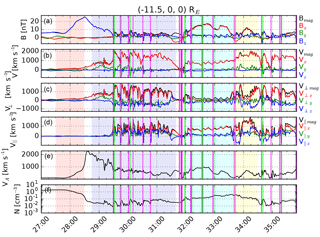
Figure 11Time series observed by a virtual satellite located at RE and in the simulation. From (a) to (f), the parameters shown are magnetic field, bulk ion velocity, bulk ion velocity perpendicular and parallel to the magnetic field, Alfvén velocity, and ion number density. The passing X and O points are indicated with the magenta and green vertical lines, respectively. Pink shading (27:30–28:30): dipolarization front. Lavender shading (28:45–31:40): fast earthward flows following the dipolarization front, with embedded X and O points. Cyan shading (32:00–33:40): plasma with enhanced ion density is fed to the plasma sheet from the lobes. Yellow shading (33:40–34:30): faster flows overtake and interact with slower flow in front of them. Note that the time axis is different from the previous plots.
3.5 Comparison of virtual and real satellite observations
3.5.1 Earthward flows
Figure 11 shows a time series observed by a virtual satellite located at RE and in the simulation. The parameters shown in the five panels are the magnetic field, bulk ion velocity, bulk ion velocity perpendicular and parallel to the magnetic field, and ion number density. The passing X and O points are indicated with the magenta and green vertical lines, respectively.
At the beginning the satellite is located near the boundary between the tail-like and dipolar field lines. Between 27:30 and 28:30 (light red shading) the satellite observes a slight decrease in Bz followed by a sharp increase of ∼20 nT. This is accompanied by a slight enhancement of N, followed by a drop from ∼1 to 0.1 cm−3, and a gradual increase in earthward velocity from zero to a few hundreds of km s−1. This signature is very similar to a dipolarization front observed by THEMIS at RE (Runov et al., 2009), except for the duration, which is seconds in the case of THEMIS and tens of seconds in Vlasiator.
The passage of the dipolarization front is followed by fast earthward flows with embedded X and O points. The flows are quite structured: at timescales of minutes they form peaks exceeding the limit of 400 km s−1 (e.g., lavender shading at 28:45–31:40). These in turn consist of peaks up to 2000 km s−1 with timescales of seconds. These short velocity peaks have a sharp increase at the leading edge, followed by a more gradual decrease. Minor X points typically coincide with the local velocity minima, indicating that the variations in the velocity are due to interaction between the outflows from the minor X points. O points often coincide with the leading edges of the local velocity maxima following the minor X points. Location of O points (cf. flux ropes) near the leading edges of the flow bursts is in agreement with satellite observations (Slavin et al., 2003).
Comparison of the total, perpendicular, and parallel Vx shows that mostly there is not much difference between Vx and , except at the X points, where the magnetic field strength is small, resulting in fluctuous direction of the B vector. The cyan shading in the plot at 32:00–33:40 approximately indicates an interval when the ion density of the lobe plasma is enhanced (Palmroth et al., 2017). During this time, Bx strengthens, indicating that the plasma sheet has moved below the z=0 plane. Consequently, is almost zero and the velocity is parallel to the magnetic field. Due to the lower Alfvén speed of the incoming plasma, the outflows (Vx) are also generally slower during this period than at other times. The change can be seen in Animation S1 in the Supplement as well. The local minima and maxima in Vx caused by minor X points are clearly weaker during this time than the period shaded in lavender. They appear more as ripples than flow peaks.
After the ion density enhancement of the lobe plasma has passed, the flow speed picks up again. The interaction region between the slower and faster flows is approximately indicated by the yellow shading at 33:40–34:30. It is characterized by an enhancement in Vy. Positive Vy is typically observed by satellites for ion flows in the midnight sector (Juusola et al., 2011a).
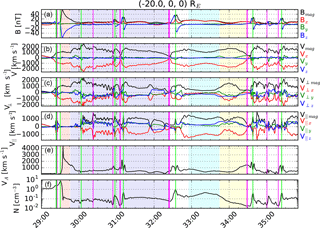
Figure 12The same as Fig. 11 except for a satellite located at RE. The pink shading (29:30–29:46) indicates the plasmoid and the lavender shading (29:46–32:25) fast tailward flows following the plasmoid. The cyan shading (32:55–33:45) and yellow shading (33:45–34:30) have the same meaning as in Fig. 11. Note that the time axis is different from the previous plots.
The O points lie in the middle of magnetic field structures typical for magnetic islands (2-D flux ropes): a bipolar structure in Bz and a peak in Bx. The Bz variations are asymmetric from −3.3 nT (leading peak, medium value) to 5.2 nT (trailing peak). The peak has a median amplitude of 8.2 nT, indicating that the centers of the magnetic islands are generally not located exactly at z=0. We have used twice the distance between an O–X pair as a proxy for the diameter of the earthward moving magnetic island. This yielded a median diameter of 0.74 RE, which could be considered a lower limit due to the asymmetries of the bipolar signatures and the offsets of the magnetic islands away from the z=0 line. The median speed of the earthward moving O points is 770 km s−1 and the signature duration 2.8 s. The values are more or less in agreement with observations (Slavin et al., 2003, 2005) cited in the Introduction, except for the shorter signature duration of the simulated structures. The time between successive magnetic islands varies, but can be as short as 15 s.
The magnetic islands are associated with an ion density peak, which is not in agreement with observations that typically show a decrease in plasma density. In the absence of the 3-D flux rope structure observed as an additional By peak and associated high magnetic pressure, the 2-D simulation balances the inward-pointing magnetic field curvature force with an enhanced plasma pressure.
3.5.2 Tailward flows
Figure 12 is the same as Fig. 11 except that the virtual satellite in this plot is located at RE. The plasmoid is indicated by the light red shading at 29:30–29:46. Both the plasmoid signature and the dipolarization signature in Fig. 11 consist of a single peak in Bz, negative in the case of the plasmoid (although there is a small positive precursor due to flux pile-up) and positive in the case of dipolarization. This is not the only difference compared to the bipolar signatures of the magnetic islands: the unipolar signatures are also longer-lasting, more intense, and associated with a clear drop in the ambient ion density (the precursor Bz signatures are associated with a density increase, indicating compressed plasma in front of the flow). They are associated with the onset of reconnection, while magnetic islands are observed later. If there was a major X point tailward of the onset site, the unipolar plasmoid signature would naturally become that of a large magnetic island. The median speed of the tailward moving plasmoid is 440 km s−1, roughly in agreement with the 350 km s−1 observed by Ieda et al. (1998).
Figure 12 shows that Vx has a significant component parallel to the magnetic field at most times, due to the nonzero Bx. This indicates that the plasma sheet is not located at the z=0 plane, but alternately above (Bx>0) or below (Bx<0) it.
Similarly to Fig. 11, the fast flows following the plasmoid (lavender shading at 29:46–32:25) are quite structured. Most of the X–O pairs have already decayed, so this must be due to residual effects. Only the largest magnetic islands survive this far. Flows between 31:00 and 34:00 are mainly produced by tailward retreating major X points (Fig. 3). As new X–O pairs do not generally emerge tailward of such X points, the resulting flows are clearly less structured than those occurring before 31:00 or after 34:00.
In general, tailward moving magnetic islands tend to be larger and more symmetrical than the earthward moving ones, in agreement with Slavin et al. (2003). The Bz variation is from 9.3 nT (leading peak, median value) to −10.9 nT (trailing peak). The median value of the peak is 8.6 nT, the speed 710 km s−1, the diameter 1.7 RE, and signature duration 9.1 s.
We have examined the substructure of BBF-type flow events produced by multiple X point near-Earth tail reconnection in Vlasiator. The flow event in the fast solar wind and southward IMF Vlasiator run agrees in many aspects with the observations recorded in the literature: tail reconnection starts to produce fast flows after the increasing pressure in the lobes has caused the plasma sheet to thin sufficiently. The fast ion bulk flows occur as 1 min timescale intensifications. A dipolarization front is observed at the leading edge of the earthward bursty flow event, a plasmoid at the leading edge of the tailward flow event, and magnetic islands at the leading edges of the individual flow bursts. While outflows from one of a few simultaneously existing major X points determine the earthward or tailward direction of the flows, and interaction between these X points can lead to changes in the flow direction at a given location, interaction between minor X points carried by the ambient flow produces the 1 min timescale substructure in the fast flows. The minor X points are associated with the magnetic islands such that an X point is always located at the leading edge of an island. The minor X point coincides with a local velocity minimum, which places the associated magnetic island at the leading edge of the following flow burst.
During the 8 min the simulation continues after the flows have started, fast flows are constantly produced in the tail, although the location in x from which the flows originate varies with time. Thus, intermittent or spatially variable (in y) reconnection does not play a role in our event. Variations in the incoming lobe plasma cause a longer timescale (several minutes) variation in the speed of the produced flows, indicating that while the 1 min timescale variations may be purely of internal origin, in longer timescale variations, including the 10 min timescale of BBFs, external drivers may play a role. However, internal effects (e.g., large-scale dipolarization) cannot be ruled out based on our analysis, as it is based on a relatively short simulation without the third spatial dimension.
Our results are in good agreement with earlier simulation work. To give some examples: Birn et al. (1996) used MHD simulations of the magnetotail to demonstrate a connection between plasmoid formation and the dipolarization of the inner magnetosphere. Wiltberger et al. (2015) showed that in a global MHD simulation, high-speed flows driven by spatially and temporally localized reconnection are present throughout the magnetotail. The flow peaks are preceded by an enhancement in Bz and a decrease in density. The global MHD simulation run by Ge et al. (2011) showed rebound oscillations of intruding BBFs and interaction between plasmas emanating from multiple X lines. Ohtani et al. (2004) conducted local two-fluid simulations of magnetic reconnection. In their simulations, fragmentation of the current sheet resulted in the formation of multiple X lines. One of the X lines dominated, establishing the overall reconnection flow pattern. Each of the X lines generated its own set of flows which were superimposed on the global flow structure created by the dominant X line. Magnetic islands formed between the X lines were swept downstream by the process. A virtual satellite observed a passing magnetic island as a bipolar signature in Bz associated with a density enhancement. Two-dimensional PIC simulations initiated from a Harris current sheet have successfully reproduced many of the observed signatures of dipolarization fronts (e.g., Sitnov et al., 2009; Eastwood et al., 2015; Goldman et al., 2016). All of these features are reproduced self-consistently in our global 2-D Vlasiator simulation. We have analyzed the motion of multiple X points as well, and shown how the various observed features of plasma flows and magnetic field structures can be understood in terms of the onset of multiple X point near-Earth tail reconnection.
Like all models and instruments, Vlasiator has shortcomings that limit its capabilities. The most obvious limitation compared to other existing models is the currently missing third spatial dimension (will be included in upcoming versions of the code), due to the heavy computational load of running a global hybrid-Vlasov simulation. For the same reason, at present the simulations have to be kept relatively short in duration. The selected spatial and temporal resolution as well as the boundary conditions of the model, particularly the lack of a realistic ionosphere, will affect the results. Finally, the physics of the current model do not include electron kinetics. Electron kinetics are known to be important in collisionless reconnection (e.g., Daughton et al., 2011; Egedal et al., 2012; Lapenta et al., 2015; Burch and Phan, 2016; Goldman et al., 2016; Torbert et al., 2016). Below we will discuss some of the observed effects of these limitations.
In 2-D, reconnection is always antiparallel reconnection, which may have a reconnection rate a factor of 10 higher than component reconnection (Fuselier et al., 2010). As there is no possibility for magnetic flux to divert past an obstacle, all incoming flux must reconnect, both at the magnetopause and in the tail. This, together with the relatively high solar wind speed and low density, might explain the plasma sheet ion flow speeds that, although realistic, tend to be somewhat on the high end of the observed range (i.e., ∼ 2000 km s−1). The speeds of the O and X points are slightly higher than those observed by spacecraft as well. Furthermore, without artificially enhanced diffusion, reconnection regions in global-scale numerical simulations tend to collapse to the width of one grid cell, and Vlasiator is no exception. Reconnection rate in such a narrow reconnection region is higher than if the region were wider (Hoilijoki et al., 2017), and might thus produce faster outflows.
A 2-D polar plane simulation cannot properly produce the Dungey (1961) cycle either, as the return of the closed magnetic flux from the nightside to the dayside is not possible. Furthermore, as already discussed in Sect. 3.5.1, flux ropes in 2-D are substituted with magnetic islands with high-density cores.
Many phenomena related to substorm physics cannot be modeled in 2-D (Palmroth et al., 2017). These include instabilities associated with the current disruption model of the substorm onset (Lui, 1996) as well as the substorm current wedge itself (McPherron et al., 1973). We do not observe clear signatures of tailward expansion of the dipolarization region. It is possible that this is a 2-D effect as well. It might be that the dipolarization region cannot grow directly under the dynamic pressure of the fast flow, but would take place in regions adjacent to the flow channel. Although the simulation allows velocities and fields in 3-D, the 2-D space limits the behavior of the plasma sheet flows. Their interaction (e.g., faster flows overtaking slower flows) is not entirely realistic, as the flows cannot meander past obstacles.
Lobe reconnection in the simulation starts very close to the transition region between tail-like and dipolar magnetic fields, at RE. Satellite observations indicate typical locations around RE (Miyashita et al., 2009). Although there are many examples of onsets occurring closer to the Earth, even at RE (e.g., Sergeev et al., 2012), it is not clear whether the simulation represents such an event (e.g., due to its fast solar wind flow conditions) or whether the onset location is a limitation of the simulation, possibly because of the 2-D space. According to Imber et al. (2011), initiation of reconnection closer to the Earth ( RE as opposed to RE) is associated with elevated solar wind speed and enhanced southward IMF. The location of the reconnection onset will naturally affect the characteristics of the resulting plasma sheet flows, particularly those propagating toward the dipole boundary.
Of the boundary conditions of the simulation, the most significant effect may be caused by the lack of a realistic ionosphere. As the open and closed magnetic field lines have their footprints in the ionosphere, the conditions in the ionosphere would be expected to affect the behavior of these field lines in the magnetosphere as well. This included the magnetic flux carried by the fast ion bulk flows and the development of the large-scale dipolarization.
Plasma sheet flows have been studied using local simulations (e.g., Birn et al., 1999), but a global simulation allows more realistic boundary conditions for the tail reconnection. Vlasiator is a young model and under rigorous development. In the coming years, the model will have a 3-D space and a realistic ionosphere. In the meantime, we can use the limited simulation to study isolated aspects of the near-Earth plasma physics, and thus gain understanding of their role in the global picture. Our results indicate that the simulation can reproduce the structured fast ion flows in the tail plasma sheet reasonably well.
We have used a polar plane simulation from the hybrid-Vlasov model, Vlasiator, driven by steady southward IMF and fast solar wind, to study fast plasma sheet ion flows and related magnetic field structures in the Earth's magnetotail. About 28 min after the start of the simulation, increasing pressure in the lobes causes the plasma sheet to thin sufficiently and tail reconnection, characterized by multiple X points, starts to produce fast earthward and tailward ion flows. The simulation ends 8 min after the onset of fast flows. Thus, we concentrated on examining the internal structure of BBF-type fast flow events. Because the solar wind remains steady throughout the simulation, we are able to rule out any external triggers and concentrate on internal processes. Our main results are as follows.
-
Ion kinetics might be sufficient to describe the behavior of plasma sheet bulk ion flows produced by tail reconnection in global near-Earth simulations. The characteristics of the fast plasma sheet flows and the embedded magnetic structures produced by Vlasiator are in general agreement with spacecraft measurements reported in the literature.
-
The structuring of the flows is caused by internal processes: while interactions between major X points determine the earthward or tailward direction of the flow, interactions between minor X points, associated with leading edges of magnetic islands carried by the flow, induce local minima and maxima in the flow speed.
-
Earthward moving flows are stopped and diverted duskward in an oscillatory (bouncing) manner at the transition region between tail-like and dipolar magnetic fields, in agreement with measurements reported in the literature. Increasing and decreasing dynamic pressure of the flows causes the transition region to shift earthward and tailward, respectively.
-
The leading edge of the train of earthward flow bursts is associated with an earthward propagating dipolarization front, while the leading edge of the train of tailward flow bursts is associated with a tailward propagating plasmoid. Impact of the dipolarization front with the dipole field causes magnetic field variations in the Pi2 range.
-
Major X points can move either earthward or tailward, although tailward motion is more common. They are generally not advected by the ambient flow. Instead, their velocity is better described by local parameters, such that an X point moves in the direction of increasing reconnection electric field strength, as has been described by Murphy et al. (2015).
Vlasiator is an open-source code released under the GPLv2 license. The code is available at http://github.com/fmihpc/vlasiator (last access: 4 September 2018).
The supplement related to this article is available online at: https://doi.org/10.5194/angeo-36-1183-2018-supplement.
LJ carried out most of the analysis and prepared the manuscript. SH provided the X and O point locations and suggested comparing their motion with Murphy (2010). YPK participated in running the simulation and developing the analysis methods. UG and RJ participated in development of the analysis methods. MB, EK, and LT participated in discussing the results. MP suggested the topic. All co-authors read the manuscript and commented on it.
The authors declare that they have no conflict of interest.
We acknowledge the European Research Council for Starting grant
200141-QuESpace, with which Vlasiator
(http://www.physics.helsinki.fi/vlasiator, last access:
4 September 2018) was developed, and Consolidator
grant 682068-PRESTISSIMO awarded for further development of Vlasiator and its
use in scientific investigations. We gratefully acknowledge Academy of
Finland grant numbers 267144 and 267186. PRACE (http://www.prace-ri.eu,
last access: 4 September 2018) is acknowledged for
granting us Tier-0 computing time in HLRS Stuttgart, where Vlasiator was run
in the HazelHen machine with project number 2014112573. Emilia Kilpua
acknowledges Academy of Finland project 1310445. The work of Lucile Turc is
supported by a Marie Sklodowska-Curie Individual Fellowship (no.
704681).
The topical editor, Elias Roussos, thanks three
anonymous referees for help in evaluating this paper.
Alexandrova, A., Nakamura, R., Semenov, V. S., and Nakamura, T. K. M.: Motion of reconnection region in the Earth's magnetotail, Geophys. Res. Lett., 42, 4685–4693, https://doi.org/10.1002/2015GL064421, 2015. a, b, c, d
Alexandrova, A., Nakamura, R., Panov, E. V., Sasunov, Y. L., Nakamura, T., Vörös, Z., Retinò, A., and Semenov, V. S.: Two interacting X lines in magnetotail: Evolution of collision between the counterstreaming jets, Geophys. Res. Lett., 43, 7795–7803, https://doi.org/10.1002/2016GL069823, 2016. a
Angelopoulos, V., Baumjohann, W., Kennel, C., Coroniti, F., Kivelson, M., Pellat, R., Walker, R., Lühr, H., and Paschmann, G.: Bursty Bulk Flows in the Inner Central Plasma Sheet, J. Geophys. Res., 97, 4027–4039, 1992. a, b
Angelopoulos, V., Kennel, C., Coroniti, F., Pellat, R., Kivelson, M., Walker, R., Russell, C., Baumjohann, W., Feldman, W., and Gosling, J.: Statistical Characteristics of Bursty Bulk Flow Events, J. Geophys. Res., 99, 21257–21280, 1994. a, b
Baker, D. N., Pulkkinen, T. I., Angelopoulos, V., Baumjohann, W., and McPherron, R. L.: Neutral line model of substorms: Past results and present view, J. Geophys. Res., 101, 12975–13010, 1996. a
Baumjohann, W., Paschmann, G., and Cattell, C.: Average Plasma Properties in the Central Plasma Sheet, J. Geophys. Res., 94, 6597–6606, 1989. a, b
Baumjohann, W., Paschmann, G., and Lühr, H.: Characteristics of High-Speed Ion Flows in the Plasma Sheet, J. Geophys. Res., 95, 3801–3809, 1990. a
Baumjohann, W., Hesse, M., Kokubun, S., Mukai, T., Nagai, T., and Petrukovich, A. A.: Substorm dipolarization and recovery, J. Geophys. Res., 104, 24995–25000, https://doi.org/10.1029/1999JA900282, 1999. a, b
Birn, J., Hesse, M., and Schindler, K.: MHD simulations of magnetotail dynamics, J. Geophys. Res., 101, 12939–12954, https://doi.org/10.1029/96JA00611, 1996. a
Birn, J., Hesse, M., Haerendel, G., Baumjohann, W., and Shiokawa, K.: Flow braking and the substorm current wedge, J. Geophys. Res., 104, 19895–19903, https://doi.org/10.1029/1999JA900173, 1999. a, b, c
Birn, J., Drake, J. F., Shay, M. A., Rogers, B. N., Denton, R. E., Hesse, M., Kuznetsova, M., Ma, Z. W., Bhattacharjee, A., Otto, A., and Pritchett, P. L.: Geospace Environmental Modeling (GEM) Magnetic Reconnection Challenge, J. Geophys. Res.-Space, 106, 3715–3719, https://doi.org/10.1029/1999JA900449, 2001. a
Birn, J., Nakamura, R., Panov, E. V., and Hesse, M.: Bursty bulk flows and dipolarization in MHD simulations of magnetotail reconnection, J. Geophys. Res., 116, A01210, https://doi.org/10.1029/2010JA016083, 2011. a
Büchner, J., Kuznetsova, M., and Zelenyi, L. M.: Sheared field tearing mode instability and creation of flux ropes in the Earth magnetotail, Geophys. Res. Lett., 18, 385–388, https://doi.org/10.1029/91GL00235, 1991. a
Burch, J. L. and Phan, T. D.: Magnetic reconnection at the dayside magnetopause: Advances with MMS, Geophys. Res. Lett., 43, 8327–8338, https://doi.org/10.1002/2016GL069787, 2016. a
Chen, C. X. and Wolf, R. A.: Theory of thin-filament motion in Earth's magnetotail and its application to bursty bulk flows, J. Geophys. Res., 104, 14613–14626, 1999. a
Chen, Y., Tóth, G., Cassak, P., Jia, X., Gombosi, T. I., Slavin, J. A., Markidis, S., Peng, I. B., Jordanova, V. K., and Henderson, M. G.: Global three-dimensional simulation of Earth's dayside reconnection using a two-way coupled magnetohydrodynamics with embedded particle-in-cell model: Initial results, J. Geophys. Res.-Space, 122, 10318–10335, https://doi.org/10.1002/2017JA024186, 2017. a
Coroniti, F. V.: On the tearing mode in quasi-neutral sheets, J. Geophys. Res., 85, 6719–6728, https://doi.org/10.1029/JA085iA12p06719, 1980. a
Daldorff, L. K. S., Tóth, G., Gombosi, T. I., Lapenta, G., Amaya, J., Markidis, S., and Brackbill, J. U.: Two-way coupling of a global Hall magnetohydrodynamics model with a local implicit particle-in-cell model, J. Comput. Phys., 268, 236–254, https://doi.org/10.1016/j.jcp.2014.03.009, 2014. a
Daughton, W., Roytershteyn, V., Karimabadi, H., Yin, L., Albright, B. J., Bergen, B., and Bowers, K. J.: Role of electron physics in the development of turbulent magnetic reconnection in collisionless plasmas, Nat. Phys., 7, 539–542, https://doi.org/10.1038/nphys1965, 2011. a
Dungey, J. W.: Interplanetary Magnetic Field and the Auroral Zones, Phys. Rev. Lett., 6, 47–48, 1961. a
Eastwood, J. P., Phan, T. D., Øieroset, M., and Shay, M. A.: Average properties of the magnetic reconnection ion diffusion region in the Earth's magnetotail: The 2001–2005 Cluster observations and comparison with simulations, J. Geophys. Res., 115, A08215, https://doi.org/10.1029/2009JA014962, 2010. a
Eastwood, J. P., Phan, T. D., Fear, R. C., Sibeck, D. G., Angelopoulos, V., Øieroset, M., and Shay, M. A.: Survival of flux transfer event (FTE) flux ropes far along the tail magnetopause, J. Geophys. Res., 117, A08222, https://doi.org/10.1029/2012JA017722, 2012. a
Eastwood, J. P., Goldman, M. V., Hietala, H., Newman, D. L., Mistry, R., and Lapenta, G.: Ion reflection and acceleration near magnetotail dipolarization fronts associated with magnetic reconnection, J. Geophys. Res.-Space, 120, 511–525, https://doi.org/10.1002/2014JA020516, 2015. a
Egedal, J., Daughton, W., and Le, A.: Large-scale electron acceleration by parallel electric fields during magnetic reconnection, Nat. Phys., 8, 321–324, https://doi.org/10.1038/nphys2249, 2012. a
Fuselier, S. A., Petrinec, S. M., and Trattner, K. J.: Antiparallel magnetic reconnection rates at the Earth's magnetopause, J. Geophys. Res., 115, A10207, https://doi.org/10.1029/2010JA015302, 2010. a
Ge, Y. S., Raeder, J., Angelopoulos, V., Gilson, M. L., and Runov, A.: Interaction of dipolarization fronts within multiple bursty bulk flows in global MHD simulations of a substorm on 27 February 2009, J. Geophys. Res., 116, A00I23, https://doi.org/10.1029/2010JA015758, 2011. a
Goldman, M. V., Newman, D. L., and Lapenta, G.: What Can We Learn about Magnetotail Reconnection from 2D PIC Harris-Sheet Simulations?, Space Sci. Rev., 199, 651–688, https://doi.org/10.1007/s11214-015-0154-y, 2016. a, b
Hoilijoki, S., Palmroth, M., Walsh, B. M., Pfau-Kempf, Y., von Alfthan, S., Ganse, U., Hannuksela, O., and Vainio, R.: Mirror modes in the Earth's magnetosheath: Results from a global hybrid-Vlasov simulation, J. Geophys. Res.-Space, 121, 4191–4204, https://doi.org/10.1002/2015JA022026, 2016. a
Hoilijoki, S., Ganse, U., Pfau-Kempf, Y., Cassak, P. A., Walsh, B. M., Hietala, H., von Alfthan, S., and Palmroth, M.: Reconnection rates and X line motion at the magnetopause: Global 2D-3V hybrid-Vlasov simulation results, J. Geophys. Res.-Space, 122, 2877–2888, https://doi.org/10.1002/2016JA023709, 2017. a, b, c, d, e, f, g, h
Ieda, A., Machida, S., Mukai, T., Saito, Y., Yamamoto, T., Nishida, A., Terasawa, T., and Kokubun, S.: Statistical analysis of the plasmoid evolution with Geotail observation, J. Geophys. Res., 103, 4453–4465, https://doi.org/10.1029/97JA03240, 1998. a, b, c
Imber, S. M., Slavin, J. A., Auster, H. U., and Angelopoulos, V.: A THEMIS survey of flux ropes and traveling compression regions: Location of the near-Earth reconnection site during solar minimum, J. Geophys. Res., 116, A02201, https://doi.org/10.1029/2010JA016026, 2011. a, b, c, d, e, f
Juusola, L., Østgaard, N., and Tanskanen, E.: Statistics of plasma sheet convection, J. Geophys. Res., 116, A08201, https://doi.org/10.1029/2011JA016479, 2011a. a, b, c
Juusola, L., Østgaard, N., Tanskanen, E., Partamies, N., and Snekvik, K.: Earthward plasma sheet flows during substorm phases, J. Geophys. Res., 116, A10228, https://doi.org/10.1029/2011JA016852, 2011b. a, b
Juusola, L., Kubyshkina, M., Nakamura, R., Pitkänen, T., Amm, O., Kauristie, K., Partamies, N., Rème, H., Snekvik, K., and Whiter, D.: Ionospheric signatures of a plasma sheet rebound flow during a substorm onset, J. Geophys. Res.-Space, 118, 350–363, https://doi.org/10.1029/2012JA018132, 2013. a
Karlsson, T., Hamrin, M., Nilsson, H., Kullen, A., and Pitkänen, T.: Magnetic forces associated with bursty bulk flows in Earth's magnetotail, Geophys. Res. Lett., 42, 3122–3128, https://doi.org/10.1002/2015GL063999, 2015. a
Kempf, Y., Pokhotelov, D., Gutynska, O., III, L. B. W., Walsh, B. M., von Alfthan, S., Hannuksela, O., Sibeck, D. G., and Palmroth, M.: Ion distributions in the Earth's foreshock: Hybrid-Vlasov simulation and THEMIS observations, J. Geophys. Res.-Space, 120, 3684–3701, https://doi.org/10.1002/2014JA020519, 2015. a
Lapenta, G., Markidis, S., Divin, A., and Goldman, D. N. M.: Separatrices: The crux of reconnection, J. Plasma Phys., 81, 325810109, https://doi.org/10.1017/S0022377814000944, 2015. a
Lui, A. T. Y.: Current disruption in the Earth's magnetosphere: Observations and models, J. Geophys. Res., 101, 13067–13088, https://doi.org/10.1029/96JA00079, 1996. a
McPherron, R. L., Russell, C. T., and Aubry, M. P.: 9. Phenomenological Model for Substorms, J. Geophys. Res., 78, 3131–3149, 1973. a, b, c
McPherron, R. L., Hsu, T.-S., Kissinger, J., Chu, X., and Angelopoulos, V.: Characteristics of plasma flows at the inner edge of the plasma sheet, J. Geophys. Res., 116, A00I33, https://doi.org/10.1029/2010JA015923, 2011. a
Miyashita, Y., Machida, S., Kamide, Y., Nagata, D., Liou, K., Fujimoto, M., Ieda, A., Saito, M. H., Russell, C. T., Christon, S. P., Nosé, M., Frey, H. U., Shinohara, I., Mukai, T., Saito, Y., and Hayakawa, H.: A state-of-the-art picture of substorm-associated evolution of the near-Earth magnetotail obtained from superposed epoch analysis, J. Geophys. Res., 114, A01211, https://doi.org/10.1029/2008JA013225, 2009. a, b, c, d, e, f
Murphy, N. A.: Resistive magnetohydrodynamic simulations of X-line retreat during magnetic reconnection, Phys. Plasmas, 17, 112310, https://doi.org/10.1063/1.3494570, 2010. a, b, c
Murphy, N. A., Parnell, C. E., and Haynes, A. L.: The appearance, motion, and disappearance of three-dimensional magnetic null points, Phys. Plasmas, 22, 102–117, https://doi.org/10.1063/1.4934929, 2015. a, b, c
Myllys, M., Kilpua, E., and Pulkkinen, T.: Solar-wind control of plasma sheet dynamics, Ann. Geophys., 33, 845–855, https://doi.org/10.5194/angeo-33-845-2015, 2015. a
Nakamura, R., Baumjohann, W., Panov, E., Petrukovich, A. A., Angelopoulos, V., Volwerk, M., Magnes, W., Nishimura, Y., Runov, A., Russell, C. T., Weygand, J. M., Amm, O., Auster, H., Bonnell, J., Frey, H., Larson, D., and McFadden, J.: Flux transport, dipolarization, and current sheet evolution during a double-onset substorm, J. Geophys. Res., 116, A00I36, https://doi.org/10.1029/2010JA015865, 2011. a
Nakamura, R., Baumjohann, W., Panov, E., Volwerk, M., Birn, J., Artemyev, A., Petrukovich, A. A., Amm, O., Juusola, L., Kubyshkina, M. V., Apatenkov, S., Kronberg, E. A., Daly, P. W., Fillingim, M., Weygand, J. M., Fazakerley, A., and Khotyaintsev, Y.: Flow bouncing and electron injection observed by Cluster, J. Geophys. Res.-Space, 118, 2055–2072, https://doi.org/10.1002/jgra.50134, 2013. a
Nakamura, T. K. M., Fujimoto, M., and Sekiya, H.: Interaction of multiple magnetic islands in a long current sheet: Two-fluid simulations, Geophys. Res. Lett., 37, L02103, https://doi.org/10.1029/2009GL041858, 2010. a
Ohtani, S., Takahashi, K., Zanetti, L. J., Potemra, T. A., McEntire, R. W., and Iijima, T.: Initial signatures of magnetic field and energetic particle fluxes at tail Reconfiguration: Explosive growth phase, J. Geophys. Res., 97, 19311–19324, https://doi.org/10.1029/92JA01832, 1992. a
Ohtani, S., Shay, M. A., and Mukai, T.: Temporal structure of the fast convective flow in the plasma sheet: Comparison between observations and two-fluid simulations, J. Geophys. Res., 109, A03210, https://doi.org/10.1029/2003JA010002, 2004. a, b, c, d, e
Ohtani, S., Miyashita, Y., Singer, H., and Mukai, T.: Tailward flows with positive BZ in the near-Earth plasma sheet, J. Geophys. Res., 114, A06218, https://doi.org/10.1029/2009JA014159, 2009. a
Oka, M., Fujimoto, M., Nakamura, T. K. M., Shinohara, I., and Nishikawa, K.-I.: Magnetic Reconnection by a Self-Retreating X Line, Phys. Rev. Lett., 101, 205004, https://doi.org/10.1103/PhysRevLett.101.205004, 2008. a
Omidi, N. and Sibeck, D. G.: Flux transfer events in the cusp, Geophys. Res. Lett., 34, L04106, https://doi.org/10.1029/2006GL028698, 2007. a
Palmroth, M., Honkonen, I., Sandroos, A., Kempf, Y., von Alfthan, S., and Pokhotelov, D.: Preliminary testing of global hybrid-Vlasov simulation: Magnetosheath and cusps under northward interplanetary magnetic field, J. Atmos. Sol.-Terr. Phy., 99, 41–46, https://doi.org/10.1016/j.jastp.2012.09.013, 2013. a
Palmroth, M., Archer, M., Vainio, R., Hietala, H., Pfau-Kempf, Y., Hoilijoki, S., Hannuksela, O., Ganse, U., Sandroos, A., von Alfthan, S., and Eastwood, J. P.: ULF foreshock under radial IMF: THEMIS observations and global kinetic simulation Vlasiator results compared, J. Geophys. Res.-Space, 120, 8782–8798, https://doi.org/10.1002/2015JA021526, 2015. a, b
Palmroth, M., Hoilijoki, S., Juusola, L., Pulkkinen, T. I., Hietala, H., Pfau-Kempf, Y., Ganse, U., von Alfthan, S., Vainio, R., and Hesse, M.: Tail reconnection in the global magnetospheric context: Vlasiator first results, Ann. Geophys., 35, 1269–1274, https://doi.org/10.5194/angeo-35-1269-2017, 2017. a, b, c, d, e, f, g, h
Panov, E. V., Nakamura, R., Baumjohann, W., Angelopoulos, V., Petrukovich, A. A., Retinò, A., Volwerk, M., Takada, T., Glassmeier, K., McFadden, J. P., and Larson, D.: Multiple overshoot and rebound of a bursty bulk flow, Geophys. Res. Lett., 37, L08103, https://doi.org/10.1029/2009GL041971, 2010. a
Pfau-Kempf, Y., Hietala, H., Milan, S. E., Juusola, L., Hoilijoki, S., Ganse, U., von Alfthan, S., and Palmroth, M.: Evidence for transient, local ion foreshocks caused by dayside magnetopause reconnection, Ann. Geophys., 34, 943–959, https://doi.org/10.5194/angeo-34-943-2016, 2016. a, b, c, d
Pokhotelov, D., von Alfthan, S., Kempf, Y., Vainio, R., Koskinen, H. E. J., and Palmroth, M.: Ion distributions upstream and downstream of the Earth's bow shock: first results from Vlasiator, Ann. Geophys., 31, 2207–2212, https://doi.org/10.5194/angeo-31-2207-2013, 2013. a
Runov, A., Nakamura, R., Baumjohann, W., Treumann, R. A., Zhang, T. L., Volwerk, M., Vörös, Z., Balogh, A., Glaßmeier, K.-H., Klecker, B., Réme, H., and Kistler, L.: Current sheet structure near magnetic X-line observed by Cluster, Geophys. Res. Lett., 30, 1579, https://doi.org/10.1029/2002GL016730, 2003. a
Runov, A., Angelopoulos, V., Sitnov, M. I., Sergeev, V. A., Bonnell, J., McFadden, J. P., Larson, D., Glassmeier, K.-H., and Auster, U.: THEMIS observations of an earthward-propagating dipolarization front, Geophys. Res. Lett., 36, L14106, https://doi.org/10.1029/2009GL038980, 2009. a, b, c, d
Russell, C. T. and McPherron, R. L.: The magnetotail and substorms, Space Sci. Rev., 15, 205–266, https://doi.org/10.1007/BF00169321, 1973. a
Saito, T.: Geomagnetic pulsations, Space Sci. Rev., 10, 319–412, 1969. a, b
Schindler, K.: A theory of the substorm mechanism, J. Geophys. Res., 79, 2803–2810, https://doi.org/10.1029/JA079i019p02803, 1974. a
Sergeev, V. A., Angelopoulos, V., and Nakamura, R.: Recent advances in understanding substorm dynamics, Geophys. Res. Lett., 39, L05101, https://doi.org/10.1029/2012GL050859, 2012. a, b, c
Shiokawa, K., Baumjohann, W., and Haerendel, G.: Braking of high-speed flows in the near-Earth tail, Geophys. Res. Lett., 24, 1179–1182, 1997. a
Shiokawa, K., Baumjohann, W., Haerendel, G., Paschmann, G., Fennell, J. F., Friis-Christensen, E., Lühr, H., Reeves, G. D., Russell, C. T., Sutcliffe, P. R., and Takahashi, K.: High-speed ion flow, substorm current wedge, and multiple Pi 2 pulsations, J. Geophys. Res., 103, 4491–4507, https://doi.org/10.1029/97JA01680, 1998. a
Sitnov, M. I., Swisdak, M., and Divin, A. V.: Dipolarization fronts as a signature of transient reconnection in the magnetotail, J. Geophys. Res., 114, A04202, https://doi.org/10.1029/2008JA013980, 2009. a
Slavin, J. A., Lepping, R. P., Gjerloev, J., Fairfield, D. H., Hesse, M., Owen, C. J., Moldwin, M. B., Nagai, T., Ieda, A., and Muka, T.: Geotail observations of magnetic flux ropes in the plasma sheet, J. Geophys. Res., 108, 1015, https://doi.org/10.1029/2002JA009557, 2003. a, b, c, d, e, f, g, h, i, j
Slavin, J. A., Tanskanen, E. I., Hesse, M., Owen, C. J., Dunlop, M. W., Imber, S., Lucek, E. A., Balogh, A., and Glassmeier, K.-H.: Cluster observations of traveling compression regions in the near-tail, J. Geophys. Res., 110, A06207, https://doi.org/10.1029/2004JA010878, 2005. a, b, c, d
Snekvik, K., Tanskanen, E., Østgaard, N., Juusola, L., Laundal, K., Gordeev, E. I., and Borg, A. L.: Changes in the magnetotail configuration before near-Earth reconnection, J. Geophys. Res., 117, A02219, https://doi.org/10.1029/2011JA017040, 2012. a, b
Torbert, R. B., Burch, J. L., Giles, B. L., Gershman, D., Pollock, C. J., Dorelli, J., Avanov, L., Argall, M. R., Shuster, J., Strangeway, R. J., Russell, C. T., Ergun, R. E., Wilder, F. D., Goodrich, K., Faith, H. A., Farrugia, C. J., Lindqvist, P.-A., Phan, T., Khotyaintsev, Y., Moore, T. E., Marklund, G., Daughton, W., Magnes, W., Kletzing, C. A., and Bounds, S.: Estimates of terms in Ohm's law during an encounter with an electron diffusion region, Geophys. Res. Lett., 43, 5918–5925, https://doi.org/10.1002/2016GL069553, 2016. a
von Alfthan, S., Pokhotelov, D., Kempf, Y., Hoilijoki, S., Honkonen, I., Sandroos, A., and Palmroth, M.: Vlasiator: First global hybrid-Vlasov simulations of Earth's foreshock and magnetosheath, J. Atmos. Sol.-Terr. Phy., 120, 24–35, https://doi.org/10.1016/j.jastp.2014.08.012, 2014. a
Wiltberger, M., Merkin, V., Lyon, J. G., and Ohtani, S.: High-resolution global magnetohydrodynamic simulation of bursty bulk flows, J. Geophys. Res.-Space, 120, 4555–4566, https://doi.org/10.1002/2015JA021080, 2015. a
Yeates, A. R. and Hornig, G.: A generalized flux function for three-dimensional magnetic reconnection, Phys. Plasmas, 18, 102–118, https://doi.org/10.1063/1.3657424, 2011. a
http://www.physics.helsinki.fi/vlasiator, last access: 4 September 2018