the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Periodic self-reformation of rippled perpendicular collisionless shocks in two dimensions
Yuki Daicho
Large-scale two-dimensional (2-D) full particle-in-cell (PIC) simulations are carried out for studying periodic self-reformation of a supercritical collisionless perpendicular shock with an Alfvén–Mach number MA∼6.
Previous self-consistent one-dimensional (1-D) hybrid and full PIC simulations have demonstrated that the periodic reflection of upstream ions at the shock front is responsible for the formation and vanishing of the shock-foot region on a timescale of the local ion cyclotron period, which was defined as the reformation of (quasi-)perpendicular shocks.
The present 2-D full PIC simulations with different ion-to-electron mass ratios show that the dynamics at the shock front is strongly modified by large-amplitude ion-scale fluctuations at the shock overshoot, which are known as ripples.
In the run with a small mass ratio, the simultaneous enhancement of the shock magnetic field and the reflected ions take place quasi-periodically, which is identified as the reformation. In the runs with large mass ratios, the simultaneous enhancement of the shock magnetic field and the reflected ions occur randomly in time, and the shock magnetic field is enhanced on a timescale much shorter than the ion cyclotron period.
These results indicate a coupling between the shock-front ripples and electromagnetic microinstabilities in the foot region in the runs with large mass ratios.
Keywords. Space plasma physics (wave–particle interactions)
It has been well known since one-dimensional (1-D) particle-in-cell (PIC) simulations in the 1970s that the “shock front” at a supercritical (quasi-)perpendicular collisionless shock shows a periodic behavior. Biskamp and Welter (1972) first reported the periodic reflection of ions and the formation of a “shock foot” at a perpendicular shock, which leads to a non-stationary shock front. Later, this process was described as a periodically vanishing “leading edge of the shock” (Leroy et al., 1982; Lembege and Dawson, 1987). The term “periodic (self-)reformation” was first used by Tokar et al. (1986) and has been widely used after the finding of the periodic reformation of quasi-parallel shocks (Burgess, 1989) which is generated by a different process from the periodic reformation of (quasi-)perpendicular shocks. In the past simulation studies, reduced parameters were used due to the computational cost. However, it has been confirmed that the reformation of (quasi-)perpendicular shocks is common in 1-D simulations with various ion-to-electron mass ratios, including the real one when the Alfvén–Mach number is supercritical but relatively low (MA<10) and the ion beta is low (βi<0.4) (Scholer et al., 2003; Scholer and Matsukiyo, 2004). The reformation disappears with high Alfvén–Mach numbers (MA>100) (Shimada et al., 2010). The existence of the reformation in the two-dimensional (2-D) system was also confirmed by a full PIC simulation (Lembege and Savoini, 1992), although a small simulation system was used due to the computational cost. In 2-D simulations with a small simulation system in the shock tangential direction, the development of shock waves becomes quite similar to that in 1-D simulations. Here, we refer to such a 2-D system with a small simulation system in the shock tangential direction as a “quasi-1-D” system.
Recent development of computer technologies allows us to perform larger-scale full PIC and higher-resolution hybrid PIC simulations in multiple dimensions with a longer simulation time. These multidimensional simulation studies sometimes modify previous understanding of the physics of collisionless shocks. Hellinger et al. (2007) and Lembege et al. (2009) reported that the periodic reformation of an exactly perpendicular shock was “suppressed” with an ion-to-electron mass ratio where the shock reformation was evident in an early phase but became less evident in a later phase, while the reformation was “absent” with . In their high-resolution 2-D hybrid PIC simulation, the excitation of electron-scale whistler mode waves at the shock front was included. In their large-scale 2-D full PIC simulation, the formation of ion-scale and large-amplitude fluctuations at the shock overshoot was included, which has been known as the “ripples” that were first reported by 2-D hybrid PIC simulation studies (Winske and Quest, 1988; Lowe and Burgess, 2003).
By contrast, Yuan et al. (2009) reported that the periodic reformation was “confirmed” in their 2-D hybrid simulation of a quasi-perpendicular shock with a shock-normal angle of . They also demonstrated that the period of the reformation became longer in the 2-D simulation than in the 1-D simulation. These results contradict each other, which brings confusion to shock scientists. Although the simulation parameters of these previous works are similar, as shown in Table 1, the obtained results seem to be different from each other. Hence, the existence of the reformation of (quasi-)perpendicular shocks is still under debate, even in 2-D kinetic simulations.
In order to study the contradiction between the former (Hellinger et al., 2007; Lembege et al., 2009) and latter (Yuan et al., 2009) results, a direct comparison was made between the 2-D full PIC simulation results of quasi-perpendicular () and exactly perpendicular () shocks (Umeda et al., 2010). It was confirmed that the shock-normal angle does not affect the presence or the suppression of the reformation of (quasi-)perpendicular shocks. It was also shown that the reformation seems to be suppressed when the shock magnetic field is analyzed by averaging over the shock-tangential direction, as done by Hellinger et al. (2007) and Lembege et al. (2009). On the other hand, the reformation is present, but its period is modified by ripples when the shock magnetic field is analyzed at a local point, as done by Yuan et al. (2009).
Lembege et al. (2009)Hellinger et al. (2007)Yuan et al. (2009)Unlike (quasi-)1-D simulations, it is expected that the issue of the presence, absence, and suppression of the shock reformation of rippled (quasi-)perpendicular shocks will be related to the ion-to-electron mass ratio in multidimensional simulations, since the reformation is suppressed with and is absent with in the previous study (Lembege et al., 2009).
It is known that the mass ratio controls the types of microinstabilities in the foot region (Scholer et al., 2003; Scholer and Matsukiyo, 2004).
By using the following two dimensionless parameters, i.e., Alfvén–Mach number
and the ratio of the thermal plasma pressure to the magnetic pressure (plasma beta),
we obtain the ratio of the upstream bulk velocity ux1 to the thermal velocity vt1 as
Hereafter, the subscripts “1” and “2” denote “upstream” and “downstream”, respectively.
This equation shows that the ratio of the upstream bulk velocity to the ion thermal velocity depends only on the Alfvén–Mach number and the ion beta, which becomes larger with a larger Alfvén–Mach number and a smaller ion beta. On the other hand, the ratio of the upstream bulk velocity to the electron thermal velocity depends also on the ion-to-electron mass ratio.
It is known that relative bulk velocities among incoming ions, reflected ions, and electrons arise in the foot region due to the reflection of a part of incoming ions at the shock front. The relative velocities become a free energy source for various types of microinstabilities in the foot region (Matsukiyo and Scholer, 2003, 2006). The ratio of the relative drift velocity between ions and electrons to the electron thermal velocity controls the types of microinstabilities via electron thermal damping. Hence, the mass ratio plays a role in the full PIC simulation of (quasi-)perpendicular shocks.
We aim to study the effect of the mass ratio (i.e., microinstabilities in the foot region) on the periodic self-reformation of perpendicular collisionless shocks. We make a comparison between 2-D full PIC simulation results with different mass ratios. In Sect. 2, the simulation setup and the detailed parameters are presented. In Sect. 3, the periodic self-reformation of (quasi-)perpendicular shocks is (re)defined in accordance with the past studies. In Sect. 4, the identification of the reformation is made by using the 2-D full PIC simulation results with different mass ratios based on the definition. Section 5 gives the summary of the result and some comments on the spacecraft in situ observation of the reformation in the geophysical plasma.
We use a standard 2-D electromagnetic full PIC code with several improvements (Umeda et al., 2003; Sokolov, 2013).
A supercritical Alfvén–Mach number (MA∼6), low beta (), and perpendicular () collisionless shock as shown in Table 1 is excited by using the “relaxation method” (e.g., Leroy et al., 1981, 1982; Muschietti and Lembege, 2006; Umeda and Yamazaki, 2006), with which the simulation domain is taken in the shock-rest frame. The shocks excited with these parameters exhibit the periodic reformation of perpendicular shocks in (quasi-)1-D systems, as we show later. A reduced plasma-to-cyclotron frequency ratio and a reduced ratio of the speed of light to the electron thermal velocity are chosen due to the computational cost, which does not play any role in hybrid PIC simulations but which may modify linear dispersion relations of microinstabilities due to reflected ions in full PIC simulations.
The simulation domain is taken in the x−y plane with periodic boundaries in the y direction and absorbing boundaries (Umeda et al., 2001) in the x direction. An in-plane shock magnetic field is imposed in the y direction (By0). The plasma flow is directed in the x direction. Hence, a motional electric field is applied in the z direction.
A detailed initial setup for 2-D simulations of (quasi-)perpendicular shocks was described in our previous studies (Umeda et al., 2008, 2009, 2010, 2011, 2012a, b, 2014) and is not repeated here.
In the present study, we perform four simulation runs, A, B, C, and D, with different ion-to-electron mass ratios , 100, 256, and 625, respectively.
The grid spacing and the time step of the present simulation runs are common ( and , where λDe is the electron Debye length). For all of Runs A–D, we perform two types of runs with different sizes of the simulation domain of (labeled as “large”) and 32di1×di1 (labeled as “small”), where is the ion inertial length ( and 250λDe1 for Runs A, B, C, and D, respectively). Note that the rippled structures at the shock front are included in the “large” simulation runs but are excluded in the “small” simulation runs.
We used 25 pairs of electrons and ions per cell in the upstream region and 64 pairs of electrons and ions per cell in the downstream region, respectively, at the initial state.
The bulk flow velocity of the upstream plasma is , 1.5, 0.9375, and 0.6 for Runs A, B, C, and D, respectively. The previous studies showed that the electron cyclotron drift instability (ECDI) is driven with the parameters of Run A (Umeda et al., 2012b, 2014), which excites electrostatic waves at multiple electron cyclotron harmonic frequencies (Muschietti and Lembege, 2006, 2013). On the other hand, the modified two-stream instability (MTSI) is driven with the parameters of Runs B–D (Umeda et al., 2012a, b, 2014), which excites obliquely propagating electromagnetic whistler mode waves at a frequency between the electron cyclotron frequency and the lower hybrid resonance frequency (Matsukiyo and Scholer, 2003, 2006).
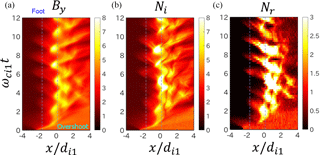
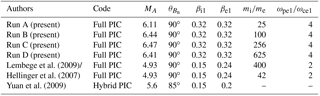
Figure 1Development of a perpendicular shock for Run A with the small simulation domain. Tangential component of the shock magnetic field By at as a function of position x and time t (a), and the corresponding ion density (b) and density of reflected ions (c). The position and time are renormalized by the ion inertial length and the ion cyclotron angular period 1∕ωci1, respectively. The magnitudes of the magnetic field and the density are normalized by the initial upstream magnetic field B01 and the initial upstream density n1. The positions of the shock foot and overshoot used in Figs. 3 and 4 are indicated by the dashed lines.
The left panel of Fig. 1 shows the tangential component of the shock magnetic field By at for Run A with the small simulation domain as a function of position x and time t. The position and time are renormalized by the ion inertial length and the ion cyclotron angular period 1∕ωci1, respectively. The magnitude is normalized by the initial upstream magnetic field B01.
The perpendicular shock generated in the simulation is at rest.
The shock overshoot (at ) shows a periodic enhancement on a timescale close to the downstream ion cyclotron period (). The shock-foot region at ) also shows the periodic vanishing, which indicates the shock reformation of the perpendicular shock.
In the middle panel of Fig. 1, we show the ion density Ni at as a function of position x and time t in the same run. The magnitude is normalized by the initial upstream density n1. We see the periodic behaviors of the ion density both at the overshoot and in the foot region. In the right panel of Fig. 1, we show the density of the reflected ion component only. Here, we obtain the density of the reflected ion by integrating the phase-space (reduced) distribution function over the velocity as
where ux2 is the downstream bulk velocity. We see the periodic behavior of the ion density in the foot region (at ).
Note that we also see these periodic behaviors in the other simulation runs (B–D) with the small simulation domain, but this is not shown here.
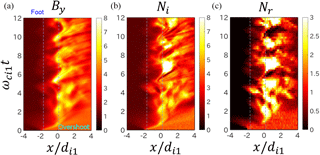
Figure 2Development of a perpendicular shock at for Run A with the large simulation domain with the same format as Fig. 1.
In Fig. 2, we show the tangential component of the shock magnetic field By, the ion density Ni, and the density of reflected ions Nr at with the same format as Fig. 1 for Run A with the large simulation domain.
The perpendicular shock generated in the simulation is at rest as in Fig. 1 (the other runs are as well, but these are not shown here). The results of the large-scale simulation run look similar to those of the small-scale simulation run until ωci1t∼4, but become different after ωci1t∼4 because of the generation of ripples.
We see quasi-periodic behaviors of the shock magnetic field at the overshoot () and in the foot region (). Although the periodic behaviors of the densities are also seen at the overshoot, their period seems not to correspond to the period of the shock magnetic field. The periodic behaviors in the foot region are not so clear in the ion density and in the density of reflected ions.
In the present simulations, the excited shocks are at rest, as seen in Figs. 1 and 2. Hence, the development of shock structures (i.e., overshoot and foot) can be discussed by the temporal variation at fixed positions.
To identify the periodic behaviors more clearly, we first re-define the position of the shock overshoot from the maximum of the shock magnetic field averaged for the time interval of ωci1t=4–12. Then, we estimate the typical gyroradius of reflected ions as , which is close to 1.85di1. We define the typical position (i.e., center) of the foot region as 1.5di1 away upstream from the overshoot by considering the typical spatial size of the shock ramp and the phase-space trajectory of reflected ions.
Figure 3 shows the temporal variation of the shock magnetic field By and the ion density Ni for Run A at the overshoot and in the foot region in the top and bottom panels, respectively. The result of the small-scale simulation run is plotted in the left panels, while the result of the large-scale simulation run is plotted in the right panels. The density of reflected ions is also plotted in the panels of the foot region.
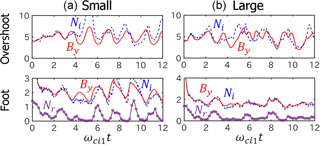
Figure 3Temporal variation of the shock magnetic field By and the ion density Ni at the overshoot and in the foot region for Run A. The left panels show the result of the small-scale simulation run (at ). The right panels show the result of the large-scale simulation run (at ). The shock overshoot is defined as a position where the shock magnetic field averaged for the time interval of ωci1t=4–12 is maximum. The shock foot is defined as a position 1.5di1 away upstream from the overshoot.
In the small-scale simulation run (left panels), periodic oscillations in both By and Ni are clearly seen at the overshoot and in the foot region. There is a positive correlation between By and Ni both at the overshoot and in the foot region. It is also seen that the shock magnetic field in the foot region increases when the shock magnetic field at the overshoot decreases (and vice versa). The result also shows that the shock magnetic field in the foot region is enhanced when the density of reflected ions is enhanced, which is identified as the reformation of (quasi-)perpendicular shocks.
In the large-scale simulation run (right panels), on the other hand, there is no relationship between the shock magnetic field at the overshoot and in the foot region. The correlation between By and Ni is positive in the foot region but not so clear at the overshoot. The result also shows that the shock magnetic field in the foot region looks enhanced when the density of reflected ions is enhanced.
Some previous 2-D simulation studies discussed the reformation of (quasi-)perpendicular shocks based on the temporal variation (periodicity) of the shock magnetic field at the overshoot. It is possible to identify the reformation from the shock magnetic field at the overshoot in 1-D simulations and in small-scale 2-D simulations (without ripples), since there is an inverse relationship between the shock magnetic field in the foot region and at the overshoot. On the other hand, the present result has clearly shown that it is not appropriate to identify the shock reformation of rippled (quasi-)perpendicular shocks only from the shock magnetic field at the overshoot of rippled shocks.
Hence, we discuss the shock reformation in terms of the quasi-periodic formation of the foot region, which is consistent with the original definition of the reformation of (quasi-)perpendicular shocks. We define the formation of the foot region by the simultaneous enhancement in the density of the reflected ions and the shock magnetic field.
As shown in the previous section, the perpendicular shocks excited in the 2-D full PIC simulations are at rest. Hence, we analyze the temporal variation of the “foot region” at a fixed position, which was defined in the previous section as 1.5di1 away upstream from the overshoot where the time-averaged By is maximum. As seen in Fig. 3, the typical characteristics of the shock reformation, i.e., the periodic oscillation of By and Nr, is well identified at this position in the run with the small simulation domain.
We detect the formation of the foot, i.e., the simultaneous enhancement of the reflected ion density and the shock magnetic field, by the following equation:
Here, 〈By〉 represents the averaged shock magnetic field for the time interval of ωci1t=4–12. This equation indicates the foot formation by taking a finite and positive value when a certain number of reflected ions exist in the foot region in association with the enhancement of the shock magnetic field by exceeding its mean value.
Figure 4 shows the temporal deviation of the shock magnetic field By from its mean value (〈By〉) together with the density of reflected ions Nr (defined in Eq. 4) in the foot region for Runs A–D with the large simulation domain. The circles show the indicator of the foot formation defined by Eq. (5).
In order to take account of the spatial variation of physical quantities in the shock tangential (y) direction due to ripples, we plot the temporal variation of the foot region at the following eight points: and 5.25.
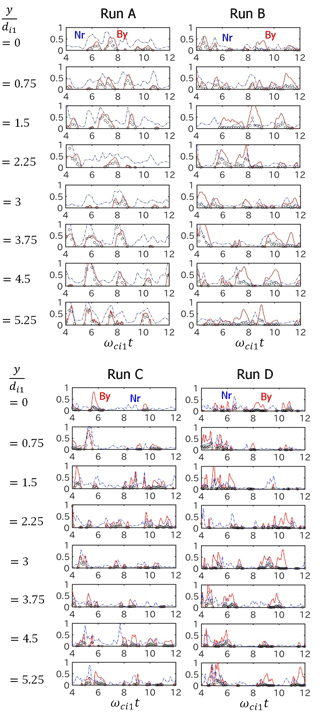
Figure 4Temporal variation of the shock magnetic field By−〈By〉 (solid lines), and density of reflected ions Nr (dash–dotted lines) in the foot region for Runs A–D with the large simulation domain. Here, 〈By〉 represents the averaged shock magnetic field for the time interval of ωci1t=4–12. The indicator of the foot formation defined in Eq. (5) is shown by circles.
In Run A (), we see the simultaneous enhancement of the shock magnetic field By and the reflected ions Nr quasi-periodically, although the periodicity is not as clear as in the run with a small simulation domain. It is shown that the enhancement of reflected ions is not necessarily accompanied by the enhancement of the shock magnetic field. The time period of the simultaneous enhancement varies in a range of ωci1Tr∼0.5–2.2, but its typical value is , which is longer than the period of the reformation in the run with the small simulation domain as demonstrated by the previous studies (Yuan et al., 2009).
In Run B (), we also see the simultaneous enhancement of the shock magnetic field By and the reflected ions Nr, but its periodicity is not as clear as in Run A. Some of the enhancement of the shock magnetic field is not related to reflected ions.
In Runs C () and D (), the simultaneous enhancement of the shock magnetic field By and the reflected ions Nr occurs almost randomly. Some of the enhancement of the shock magnetic field occurs in a timescale much shorter than the local ion cyclotron period, indicating the existence of electron-scale electromagnetic waves.
5.1 Discussions on the simulation results
Two-dimensional full PIC simulations of rippled perpendicular collisionless shocks with MA∼6 and were performed with different ion-to-electron mass ratios. The periodic self-reformation of (quasi-)perpendicular shocks was detected from the simultaneous enhancement of the shock magnetic field and the reflected ions in the foot region.
In the runs with the small simulation domain where the shock-front ripples are absent, the dynamics at the shock front was independent of the mass ratio and the periodic formation and vanishing of the foot region was clearly detected at the time period of . The periodic oscillation of the shock overshoot was also seen at the same time period.
In the runs with the large simulation domain, the shock-front ripples are present. In the run with , there was no correlation between the temporal variation of the shock magnetic field in the foot region and the overshoot, suggesting that it was not appropriate to detect the reformation of (quasi-)perpendicular shocks from the quasi-periodic oscillation of the shock magnetic field at the overshoot as done by some previous studies. The quasi-periodic formation of the foot region was detected at the typical time period of .
In the runs with , and 625 and the large simulation domain, the simultaneous enhancement of the shock magnetic field and the reflected ions occurred randomly in time at the front of the shock ramp. The enhancement of reflection ions did not necessarily correspond to the enhancement of the magnetic field that occurred at a timescale shorter than the local ion cyclotron period. These results indicate the absence of the periodic reformation of a rippled perpendicular shock.
The previous studies showed that the ion-to-electron mass ratio controlled the types of microinstabilities in the foot region (Scholer et al., 2003; Scholer and Matsukiyo, 2004). The MTSI was dominant in the foot region in the runs with , and 625 (Umeda et al., 2012b, 2014). The excitation of the whistler mode in the foot region was also indicated by the enhancement of the shock magnetic field at the timescale much shorter than the local ion cyclotron period. It was also shown that the wavelength in the shock tangential direction of the whistler mode excited by the MTSI is close to the wavelength of the ripples (Umeda et al., 2014). It is suggested that wave–wave coupling between the whistler mode and the ripples is possible, which disturbs the periodic reformation of (quasi-)perpendicular shocks.
The ECDI was driven in the run with (Umeda et al., 2012a, b, 2014). The electron cyclotron harmonic mode does not have magnetic fluctuations, and does not interact with the shock-front ripples. It is suggested that the quasi-periodic formation of the foot region is present when there is no microinstability in the foot region or when electrostatic instabilities such as ECDI and upper-hybrid drift instability are driven as seen in the previous 2-D simulations (Lembege et al., 2009; Yuan et al., 2009; Umeda et al., 2010), but its time period is modified by the shock-front ripples from the typical time period in 1-D simulations.
The present study does not deny the existence of the reformation of (quasi-)perpendicular shocks in the real space plasma, although the reformation is absent in the simulation runs of rippled perpendicular shocks with larger mass ratios. It is suggested that the existence of the periodic reformation of (quasi-)perpendicular shocks depends on the physical parameters indicated by Eq. (3). The reformation of (quasi-)perpendicular shocks could exist by suppressing the MTSI in the foot region by other instabilities as in Run A.
Since the present study used the reduced frequency ratio (and the reduced speed of light ), it is worth discussing the effect of the frequency ratio to microinstabilities at the shock foot. The frequency ratio ωp∕ωc does not affect the structure of shock on ion scales. The effect of the frequency ratio ωp∕ωc to the velocity distribution functions at the shock foot is not so large as long as the Alfvén–Mach number and the plasma beta are the same, as shown by the previous study (Umeda et al., 2012b).
Let us suppose that velocity distribution functions of electrons and ions at the shock foot are independent of the frequency ratio as indicated from Eq. (3). Then, we can use the parameters for the velocity distribution functions of a three-component plasma at the shock foot (), which were obtained from the run with (Run A of Table II) in the previous study (Umeda et al., 2012b). We change ωpe1∕ωce1 as 4, 20, and 100, and solve the linear dispersion relation. Note that (vte1ωpe1)∕(cωce1) is constant due to Eq. (2).
Figure 5 shows the dispersion relation of the MTSI. The wave-normal angle relative to the ambient magnetic field is 85∘ for kx>0 and 84∘ for kx<0. The growth rate of the MTSI for is slightly smaller than that for and 100 since the electron thermal velocity is close to the speed of light. The linear dispersion relations for and 100 are almost the same due to . The present linear analysis suggests that the effect of the frequency ratio ωp∕ωc to the linear dispersion relation of the MTSI is small.
The ECDI does not have a positive growth rate for all of the frequency ratios, suggesting that the frequency ratio ωp∕ωc does not affect the present simulation results with MA∼6 and .
It should be noted that the ECDI is dominant in a lower-beta plasma and that the frequency ratio affects the growth rate of the ECDI (Muschietti and Lembege, 2013). The ECDI can disturb the generation of the MTSI through nonlinear saturation as seen in Run A. Further self-consistent full PIC simulations are needed to study the influence of the frequency ratio on the competition between the ECDI and the MTSI. However, the size of the computational domain is proportional to (ωp∕ωc)2 and the time step is proportional to ωp∕ωc in 2-D full PIC simulation. It is a heavy task to use a large ωp∕ωc in large-scale full PIC simulations. Equation (3) also shows that a larger Mach number or a lower beta gives a large ux1∕vte1 which is necessary for driving the ECDI with a larger mass ratio.
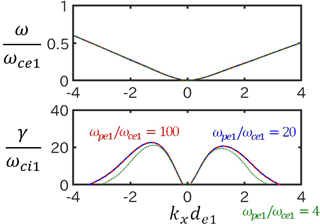
Figure 5Linear dispersion relations for a three-component plasma based on the velocity distribution functions in the foot region of a perpendicular collisionless shock () in Run A of Table II in the previous study (Umeda et al., 2012b). The frequency ratio ωpe1∕ωce1 is changed as 4 (dotted lines), 20 (dashed lines), and 100 (solid lines) by keeping vte1ωpe1∕cωce1 constant. The wave-normal angle relative to the ambient magnetic field is 85∘ for kx>0 and 84∘ for kx<0.
5.2 Discussions on the comparison with observations
Since the present simulation study used reduced parameters (mi∕me, ωpe1∕ωce1, and c∕vte1), it is not easy to compare the present study with the spacecraft in situ observations directly.
However, it is worth discussing the in situ observations of the shock reformation in the geophysical plasma by extrapolating the present simulation results. There are two references which explicitly tried to detect the reformation of (quasi-)perpendicular shocks.
Mazelle et al. (2010) made a statistical analysis of quasi-perpendicular shocks with parameters ranging for , , and βi≤0.6 observed by the Cluster spacecraft. As evidence of the reformation of (quasi-)perpendicular shocks, they showed that the spatial size of the shock ramp is less than the ion inertial length and has a Gaussian-like distribution with a standard deviation of 10 and a few electron inertial lengths.
Figure 6 shows the histogram of the spatial size of the shock ramp for 8 points in position points in time () in the present simulation run with and the large simulation domain where the periodic reformation of perpendicular shocks is not seen. Here, the spatial size of the shock ramp is approximated by the gradient of the shock magnetic field normalized by .
The spatial size of the shock ramp is distributed between 0.04di1(=de1) and 1.1di1, and its typical size is 0.16di1. The characteristics of the histogram are not the same as Fig. 6 of Mazelle et al. (2010), since the result includes the spatial size of the shock ramp for only an exactly perpendicular shock with a specific Mach number and plasma beta. However, it is clearly shown that the spatial size of the shock ramp has a distribution without the periodic reformation of perpendicular shocks. Hence, the result of Mazelle et al. (2010) showed the non-stationarity of the quasi-perpendicular shock, but did not necessarily indicate reformation.
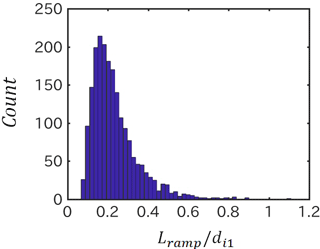
Figure 6Histogram of the spatial size of the shock ramp for 8 points in position points in time () in the run with and the large simulation domain. The spatial size of the shock ramp is approximated by the gradient of the shock magnetic field normalized by .
Lobzin et al. (2007) reported a quasi-periodic reflection of ions at the front of a quasi-perpendicular shock with MA=10, , βi=2.0, and βe=1.7 by the Cluster spacecraft. The time period for the formation of reflected ion bursts is ∼8 s that corresponds to 0.5Tci1, which is much longer than the period of the reformation seen in the present full PIC simulations. The result seemed to be consistent with the original definition of the reformation of (quasi-)perpendicular shocks, although the simultaneous enhancement of the shock magnetic field in the foot region was not shown. However, the time period of ∼8 s is close to the time resolution of the instrument (4 s). Also, it is known from the hybrid PIC simulation results that the shock front at a (quasi-)perpendicular shock with a high ion beta (βi>1) is stationary (e.g., Leroy et al., 1982; Hellinger et al., 2002). Therefore, it is unclear whether the periodic behavior identified by Lobzin et al. (2007) really exhibits the “reformation of quasi-perpendicular shocks” in its original definition.
It is possible that the periodic behavior at the shock front of quasi-perpendicular shocks is generated by whistler mode waves (Scholer and Burgess, 2007), which is similar to the reformation of quasi-parallel shocks. This process is, however, outside the scope of the present simulation study. Further PIC simulation studies with parameters similar to this event (higher Mach number and higher ion beta) are necessary.
5.3 Summary
The present 2-D full PIC simulation study reproduced the results of the previous 2-D simulations (Hellinger et al., 2007; Lembege et al., 2009; Yuan et al., 2009) by using different ion-to-electron mass ratios. It is suggested that the periodic reformation of (quasi-)perpendicular shocks is not common, unlike 1-D simulations. The reformation in its original definition exists with a narrower range of the Alfvén–Mach number and the plasma beta as well as the electron plasma-to-cyclotron frequency ratio in 2-D than in 1-D. It is not so easy to identify the reformation in multidimensional simulations even with a simplified model. It might be quite difficult to identify it from limited data obtained by in situ observation.
Access to the raw data of the present numerical simulations may be provided upon reasonable request to one of the authors (Takayuki Umeda, taka.umeda@nagoya-u.jp).
TU developed the simulation codes, drafted the manuscript, and approved the final manuscript. YD contributed to the analysis of the simulation data.
The authors declare that they have no conflict of interest.
One of the authors (Takayuki Umeda) is grateful to Yoshitaka Kidani and
Shuichi Matsukiyo for discussions. This work was supported by MEXT/JSPS under
Grant-In-Aid (KAKENHI) for Scientific Research (B) no. JP26287041. The
computer simulations were performed on the supercomputer systems at the
Institute for Space-Earth Environmental Research and the Solar-Terrestrial
Environment Laboratory in Nagoya University through a joint research
program.
The topical editor, Minna
Palmroth, thanks Yann Pfau-Kempf and two anonymous referees for help in
evaluating this paper.
Biskamp, D. and Welter, H.: Numerical studies of magnetosonic collisionless shock waves, Nucl. Fusion, 12, 663–666, 1972. a
Burgess, D.: Cyclic behavior at quasi-parallel collisionless shocks, Geophys. Res. Lett., 16, 345–348, 1989. a
Hellinger, P., Travnicek, P. M., Lembege, B., and Savoini, P.: Emission of nonlinear whistler waves at the front of perpendicular supercritical shocks: hybrid versus particle simulations, Geophys. Res. Lett., 34, L14109, https://doi.org/10.1029/2007GL030239, 2007. a, b, c, d, e
Hellinger, P., Travnicek, P., and Matsumoto, H.: Reformation of perpendicular shocks: Hybrid simulations, Geophys. Res. Lett., 29, 2234, https://doi.org/10.1029/2002GL015915, 2002. a
Lembege, B. and Dawson, J. M.: Self-consistent study of a perpendicular collisionless and nonresistive shock, Phys. Fluids, 30, 1767–1788, 1987. a
Lembege, B. and Savoini, P.: Non-stationarity of a two-dimensional quasi-perpendicular supercritical collisionless shock by self-reformation, Phys. Fluids B, 4, 3533–3548, 1992. a
Lembege, B., Savoini, P., Hellinger, P., and Travnicek, P. M.: Nonstationarity of a two-dimensional perpendicular shock: Competing mechanism, J. Geophys. Res., 114, A03217, https://doi.org/10.1029/2008JA013618, 2009. a, b, c, d, e, f, g
Leroy, M. M., Goodrich, C. C., Winske, D., Wu, C. S., and Papadopoulos, K.: Simulation of a perpendicular bow shock, Geophys. Res. Lett., 8, 1269–1272, 1981. a
Leroy, M. M., Winske, D., Goodrich, C. C., Wu, C. S., and Papadopoulos, K.: The structure of perpendicular bow shocks, J. Geophys. Res., 87, 5081–5094, 1982. a, b, c
Lowe, R. E. and Burgess, D.: The properties and causes of rippling in quasi-perpendicular collisionless shock fronts, Ann. Geophys., 21, 671–679, https://doi.org/10.5194/angeo-21-671-2003, 2003. a
Lobzin, V. V., Krasnoselskikh, V. V., Bosqued, J.-M., Pincon, J.-L., Schwartz, S. J., and Dunlop, M.: Nonstationarity and reformation of high-Mach-number quasiperpendicular shocks: Cluster observations, Geophys. Res. Lett., 34, L05107, https://doi.org/10.1029/2006GL029095, 2007. a, b
Matsukiyo, S. and Scholer, M.: Modified two-stream instability in the foot of high Mach number quasi-perpendicular shocks, J. Geophys. Res., 108, 1459, https://doi.org/10.1029/2003JA010080, 2003. a, b
Matsukiyo, S. and Scholer, M.: On microinstabilities in the foot of high Mach number perpendicular shocks, J. Geophys. Res., 111, A06104, https://doi.org/10.1029/2005JA011409, 2006. a, b
Mazelle, C., Lembege, B., Morgenthaler, A., Meziane, A., Horbury, T. S., Genot, V., Lucek, E. A., and Dandouras, I.: Self-reformation of the quasi-perpendicular shock: CLUSTER observations, in Twelfth International Solar Wind Conference, AIP Conf. Proc. Vol. 1216, 471–474, https://doi.org/10.1063/1.3395905, 2010. a, b, c
Muschietti, L. and Lembege, B.: Electron cyclotron microinstability in the foot of a perpendicular shock: A self-consistent PIC simulation, Adv. Space Res., 37, 483–493, 2006. a, b
Muschietti, L. and Lembege, B.: Microturbulence in the electron cyclotron frequency range at perpendicular supercritical shocks, J. Geophys. Res., 118, 2267–2285, 2013. a, b
Scholer, M. and Burgess, D.: Whistler waves, core ion heating, and nonstationarity in oblique collisionless shocks, Phys. Plasmas, 14, 072103, https://doi.org/10.1063/1.2748391, 2007. a
Scholer, M. and Matsukiyo, S.: Nonstationarity of quasi-perpendicular shocks: a comparison of full particle simulations with different ion to electron mass ratio, Ann. Geophys., 22, 2345–2353, https://doi.org/10.5194/angeo-22-2345-2004, 2004. a, b, c
Scholer, M., Shinohara, I., and Matsukiyo, S.: Quasi-perpendicular shocks: length scale of the cross-shock potential, shock reformation, and implication for shock surfing. J. Geophys. Res., 108, 1014, https://doi.org/10.1029/2002JA009515, 2003. a, b, c
Shimada, N., Hoshino, M., and Amano, T.: Structure of a strong supernova shock wave and rapid electron acceleration confined in its transition region, Phys. Plasmas, 17, 032902, https://doi.org/10.1063/1.3322828, 2010. a
Sokolov, I. V.: Alternating-order interpolation in a charge-conserving scheme for particle-in-cell simulations, Comput. Phys. Commun. 184, 320–328, 2013. a
Tokar, R. L., Aldrich, C. H., Forslund, D. W., and Quest, K. B.: Nonadiabatic electron heating at high-Mach-number perpendicular shocks, Phys. Rev. Lett., 56, 1059–1062, 1986. a
Umeda, T., Kidani, Y., Matsukiyo, S., and Yamazaki, R.: Modified two-stream instability at perpendicular shocks: Full particle simulations, J. Geophys. Res., 117, A03206, https://doi.org/10.1029/2011JA017182, 2012a. a, b, c
Umeda, T., Kidani, Y., Matsukiyo, S., and Yamazaki, R.: Microinstabilities at perpendicular collisionless shocks: A comparison of full particle simulations with different ion to electron mass ratio, Phys. Plasmas, 19, 042109, https://doi.org/10.1063/1.3703319, 2012b. a, b, c, d, e, f, g, h
Umeda, T., Kidani, Y., Matsukiyo, S., and Yamazaki, R.: Dynamics and microinstabilities at perpendicular collisionless shock: A comparison of large-scale two-dimensional full particle simulations with different ion to electron mass ratio, Phys. Plasmas, 21, 022102, https://doi.org/10.1063/1.4863836, 2014. a, b, c, d, e, f
Umeda, T., Kidani, Y., Yamao, M., Matsukiyo, S., and Yamazaki, R.: On the reformation at quasi- and exactly perpendicular shocks: Full particle-in-cell simulations, J. Geophys. Res. 115, A10250, https://doi.org/10.1029/2010JA015458, 2010. a, b, c
Umeda, T., Omura, Y., and Matsumoto, H.: An improved masking method for absorbing boundaries in electromagnetic particle simulations, Comput. Phys. Commun., 137, 286–299, 2001. a
Umeda, T., Omura, Y., Tominaga, T., and Matsumoto, H.: A new charge conservation method for electromagnetic particle simulations, Comput. Phys. Commun., 156, 73–85, 2003. a
Umeda, T., Yamao, M., and Yamazaki, R.: Two-dimensional full particle simulation of a perpendicular collisionless shock with a shock-rest-frame model, Astrophys. J., 681, L85–L88, 2008. a
Umeda, T., Yamao, M., and Yamazaki, R.: Electron acceleration at a low-Mach-number perpendicular collisionless shock, Astrophys. J., 695, 574–579, 2009. a
Umeda, T., Yamao, M., and Yamazaki, R.: Cross-scale coupling at a perpendicular collisionless shock, Planet. Space Sci., 59, 449–455, 2011. a
Umeda, T. and Yamazaki, R.: Particle simulation of a perpendicular collisionless shock: A shock-rest-frame model, Earth Planets Space, 58, e41–e44, 2006. a
Yuan, X., Cairns, I. H., Trichtchenko, L., Rankin, R., and Danskin, D. W.: Confirmation of quasi-perpendicular shock reformation in two-dimensional hybrid simulations, Geophys. Res. Lett., 36, L05103, https://doi.org/10.1029/2008GL036675, 2009. a, b, c, d, e, f, g
Winske, D. and Quest, K. B.: Magnetic-field and density-fluctuations at perpendicular supercritical collisionless shocks, J. Geophys. Res., 93, 9681–9693, 1988. a