the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
An optimal tropospheric tomography approach with the support of an auxiliary area
Qingzhi Zhao
Yibin Yao
Wanqiang Yao
Pengfei Xia
Among most current tropospheric tomography studies, only the signals crossing out from the top boundary of the tomographic area are used for reconstructing the three-dimensional water vapour field, while signals penetrating from the side faces of the tomographic body are ignored as invalid information. Such a method wastes the valuable Global Navigation Satellite System (GNSS) observations and decreases the utilisation efficiency of GNSS rays. This is the focus of this paper, which tries to effectively use signals penetrating from the side faces of the tomographic body for water vapour reconstruction. An optimised tropospheric tomography method is proposed using an auxiliary area. The top height of the tomography body is determined based on the average water vapour distribution derived from the Constellation Observing System for Meteorology, Ionosphere, and Climate (COSMIC) radio occultation (RO) products. In addition, the coefficients of a negative exponential function between the adjacent layers for vertical constraints are fitted using the COSMIC RO profiles. Thirteen GPS stations are selected in the CORS Network of Texas to perform the tomographic experiment and validate the performance of the proposed method at 00:00 and 12:00 UTC daily using the radiosonde data for a period of 15 days. Compared to the conventional method, the accuracy of the reconstructed water vapour information derived from the proposed method is increased by 14.37 % and 16.13 %, respectively, in terms of mean root mean square (rms) and mean absolute error (MAE). The tomographic results obtained from the proposed method are further validated with the slant water vapour (SWV) data derived using the GAMIT (GNSS processing software package). Results show that the rms and MAE accuracy of SWV values has been improved by 18.18 % and 27.62 %, respectively, when compared to the conventional method.
Keywords. History of geophysics (atmospheric sciences)
Water vapour is one of the most important factors affecting atmospheric dynamics, evolution of weather systems, and global climate change. Therefore, knowledge of the water vapour distribution at a high spatio-temporal resolution is a vital prerequisite for the prediction of medium- to small-scale weather events as well as the monitoring of climate change (Zhang et al., 2015). Traditionally, radiosonde and microwave radiometers have been used for acquiring water vapour information at a low spatio-temporal resolution with high costs and the techniques do not work in all weather conditions (Wan, 2014). To overcome the drawbacks of the conventional methods, an improved method to detect atmospheric water vapour using Global Navigation Satellite System (GNSS) technology has emerged with a high spatio-temporal resolution and low cost.
Since the concept of GNSS meteorology was first proposed by Bevis et al. (1992), various validations and applications have been reported across the globe and a root mean square (rms) error of integrated water vapour (IWV) of 1 to 2 mm using ground-based GNSS observations was achieved (e.g. Rocken et al., 1993; Duan et al., 1996; Emardson et al., 2000; Niell et al., 2001; Gendt et al., 2004; Smith et al., 2007; Raja et al., 2008; de Haan et al., 2009; Lee et al., 2013). However, to acquire three-dimensional water vapour information, the tropospheric tomography technique was introduced by taking advantage of SWV values crossing the area of interest (Flores et al., 2000; Hirahara, 2000; Bi et al., 2006; Notarpietro et al., 2011). Such a technique was first proposed in the area of medicine (Bramlet, 1978), and has been widely applied in many areas, such as geology (Bourjot and Romanowicz, 1992), earthquake analysis (Kissling et al., 1994), ionosphere modelling (Hajj et al., 1994; Rius et al., 1997), and wind analysis (Gao et al., 1999).
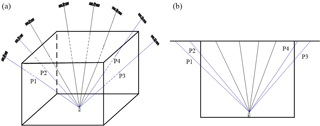
Figure 1Schematic diagram of satellite signals crossing the tomography area (a) and their front view (b), where signals P1–P4 are crossed from the side of the tomography area.
Tropospheric tomography requires that the area of interest be discretised into many voxels and using those satellite rays crossing the voxels therein (Yao and Zhao, 2016); however, many voxels are not crossed by a signal ray due to the influence of the geometric distribution of the constellation of GNSS satellites as well as the ground-based GNSS receivers (Flores et al., 2000), which leads to a problem of inversion in the tomographic resolution (Bender et al., 2011a). Normally, some constraints, such as the horizontal constraints and vertical constraints, are imposed in tomographic modelling so as to overcome rank deficiency problems (Flores et al., 2000; Bi et al., 2006; Troller et al., 2006; Rohm and Bosy, 2011; Chen and Liu, 2014; Rohm et al., 2014). Ding et al. (2018) proposed a node parameterisation approach using a combination of three meshing techniques to dynamically adjust both the boundary of the tomographic region and the position of nodes. It must be noted that the satellite rays used in the conventional tomography method refer to signals crossing out from the top side of the tomographic body, while the signals penetrating from the side faces are ignored as “unusable” information (Yao et al., 2016). To maximise the usage of the signals penetrating from the side faces of the tomographic body, some studies have been carried out in recent years. A ray-tracing water vapour model has been applied by Rohm and Bosy (2011) to estimate the outer part of the GNSS signal rays using the UNB3m model. Notarpietro et al. (2011) proposed a method to obtain the values of GNSS signals inside the tomography area by extracting the values outside the area, where the values outside the area are estimated with the support of the CIRA-Q wet atmospheric climatologic model or the ECMWF reanalysis data. The water vapour content inside the tomography area is estimated by geometrical linear estimation using an exponential negative function (Benevides et al., 2014). Yao et al. (2016) proposed a method using signals crossing out from the side faces of the tomographic body by introducing the water vapour unit index which was further improved using a more sophisticated model and additional data resources (Zhao and Yao, 2017). Chen and Liu (2016) used numerical weather prediction (NWP) profile data to calculate the water vapour content outside the tomographic sides and then obtained the value of water vapour content inside the tomographic body. However, the methods mentioned above require the availability of specific external information, which restricts the application of those methods.
In this paper, a new tropospheric tomography method is proposed by introducing an auxiliary area into the tomographic process. The introduced auxiliary area can be used to incorporate the contribution of satellite rays crossing the side faces of a tomographic body into the tomographic results. In addition, the COSMIC (Constellation Observing System for Meteorology, Ionosphere, and Climate) radio occultation products are also used for determining the top height of the tomography body as well as the coefficients of a vertical constraint formula. The proposed method is capable of using all satellite rays with a given elevation angle for water vapour reconstruction. This paper is organised as follows: Sect. 2 presents a tropospheric tomography method with the support of an auxiliary area; data processing and the determination of the top height of the tomographic body are covered in Sect. 3; in Sect. 4, the tomographic results are analysed to validate the proposed method with radiosonde data, and the discussion and conclusions are presented in Sect. 5.
2.1 Tomographic principles
Generally, two classes of tropospheric parameters estimated from ground-based GNSS observations are used for the reconstruction of the water vapour field. The first kind of input information is slant wet delay (SWD), which can be used to obtain the atmospheric wet refractivity (Flores et al., 2000; Hirahara, 2000; Skone and Hoyle, 2005; Rohm and Bosy, 2009; Notarpietro et al., 2011). The second kind of input information is slant water vapour (SWV), which can be used to reconstruct the three-dimensional water vapour density field (Champollion et al., 2005; Bi et al., 2006; Chen and Liu, 2014). The corresponding output parameters from those two methods can be mutually interconverted with the help of atmospheric temperature information (Bender et al., 2011a). In our study, the more sophisticated SWV parameters are selected as input information for a tropospheric tomography experiment.
The SWV can be described as a total water vapour content from satellite to receiver antenna along the propagation path, and can be expressed by
where ρ(s) is the water vapour density (unit: g m−3) and ds is the distance travelled by a satellite ray. According to tropospheric tomography theory, the research area is discretised into many voxels under the assumption that the water vapour density value of each voxel is unchanged during a given period. Therefore, many satellite rays with different azimuth angles and elevation angles can be used to build the observation equation governing the tomographic modelling. The relationship between SWV and water vapour density can be expressed in the matrix form below:
where y represents a column vector with many SWV values and A is a coefficient matrix of distances crossed by satellite rays, while x denotes the unknown parameter which refers to the water vapour density in our study.
Apart from the observation equation, some additional constraint equations are required to solve the rank deficiency issue arising from the inversion algorithm (Flores et al., 2000; Bender et al., 2011b; Rohm and Bosy, 2011). Usually, two different classes of constraints, the horizontal and vertical constraints, are employed in tropospheric tomography (Flores et al., 2000; Bi et al., 2006; Troller et al., 2006; Bender et al., 2001b; Rohm and Bosy, 2011; Chen and Liu, 2014). In our study, a horizontal constraint equation is established based on the assumption that the water vapour in a certain voxel is a weighted mean value of its horizontally near neighbours (Yao et al., 2017). As for the vertical constraint equation, the exponential negative function is introduced to reflect the relationship between two adjacent voxels vertically. The coefficients of the exponential negative function are fitted based on the average water vapour distribution at different altitudes derived from the COSMIC RO “wetPrf” profiles for the period of 2006 to 2016 (see Sect. 3.2). After the various constraints are combined with the observation equation, the conventional tomographic model can be obtained as
where H and V represent the coefficient matrices of horizontal and vertical constraints, respectively.
2.2 An improved tropospheric tomography method
For most current tropospheric tomography studies, only those signals passing through the entire tomographic area are used, while the signals crossing out from the side faces of the tomographic body are ignored. Such behaviour not only neglects the valuable observations, but also decreases the numbers of satellite rays usable and voxels crossed by rays. As shown in Fig. 1, blue rays P1–P4 which cross the side faces of the tomographic body cannot be used for water vapour tomography based on the conventional methods.
To incorporate the value of rays crossing the side faces of a tomography body, a novel method is proposed by introducing an auxiliary area. The main idea is that, when the tomography area is extended in latitudinal and longitudinal directions over a certain distance, the satellite rays which penetrate from the side faces of the tomographic body are crossing out from the top boundary of the surrounding area (called the auxiliary area). Therefore, the rays crossing out from the side faces of the tomographic body can be used for the reconstruction of the water vapour field. For the original tomographic area, the reconstructed water vapour density using the auxiliary area can be used as the initial water vapour field. The specific steps are presented as follows.
-
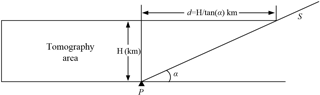
Determine the horizontal distance of horizontal extension. As shown in Fig. 2, the blue rectangle marks the research area selected for tomography, while the red rectangle is the auxiliary area. Therefore, the distance between the research area and auxiliary area is first required to be determined. Assuming that one station is located on the border of the research area, as shown by ▴ in Fig. 3, the extended distance can be calculated using the following formula:
where d is the extended distance, H is the height of the tomography area, and α is the satellite cut-off elevation angle.
-
Reconstruct the water vapour field of the auxiliary area: according to the tomographic model established in Eq. (3), the water vapour information for the auxiliary area can be obtained using GNSS measurements with elevation angles greater than α.
-
Select the water vapour density of voxels located in the tomographic area and consider those values initial constraints for the reconstruction of the water vapour field therein. Given this, a novel tomographic model for the proposed method can be established as
where I is the unit matrix of the initial constraint equation, while ρo is the initial water vapour density value of each voxel derived from the tomographic result in Step (2).
-
Singular value decomposition is used to solve Eq. (5), and the general inverse matrix can be obtained (Ran and Ge, 1997). In this way, the contribution of satellite rays which penetrate from the side faces of the tomographic body can be incorporated into the water vapour reconstruction process.
3.1 Data collection and processing
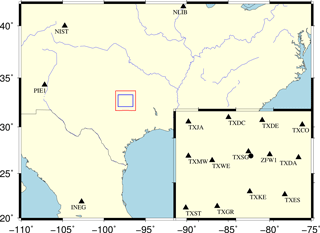
In the present study, the data from 13 ground-based stations (▴ in Fig. 2) derived from the CORS Network in Texas are selected for the period of 11 to 25 May 2015. One radiosonde station (• in Fig. 2) is located in this area, where radiosonde balloons are launched twice per day at 00:00 and 12:00 UTC, respectively. The space-based COSMIC post-processed “wetPrf” profiles provided by the University Corporation for Atmospheric Research/COSMIC Data Analysis and Archival Center (UCAR/CDAAC) are also used for the period 2006 to 2016 (http://www.cosmic.ucar.edu/, last access: September 2017). “wetPrf” profiles include the latitude and longitude of the perigee point, refractivity, temperature, pressure, and mean sea level altitude from the surface to 40 km (Hudnut et al., 2007). The parameters provided by “wetPrf” profiles are interpolated at altitude intervals of 100 m and calculated by the non-standard 1DVar (one-dimensional variational) technique (Hudnut et al., 2007).
The research area is divided as follows: latitude ranges from 32.1 to 33.3∘ N in steps of 0.2∘ and longitude ranges from 96.5 to 98.3∘ W in steps of 0.3∘. The top height of the tomographic body is at an elevation of 10 km with steps of 1 km, which is determined based on the average water vapour variations with altitude from COSMIC “wetPrf” profiles. Consequently, there is a total of voxels obtained in our study. The satellite cut-off elevation angle is selected as 10∘; therefore, the auxiliary area can be determined based on the method proposed in Sect. 2.2 with a latitude range from 31.7 to 33.7∘ N, a longitude range from 96.2∘ W to 98.6∘ W, and a total of voxels.
The ground-based GPS observations for the experiment period of 15 days are processed with GAMIT/GLOBK (v10.5) (Herring et al., 2010). The zenith total delay (ZTD) parameter and wet delay gradients in the east–west and north–south directions are estimated at intervals of 0.5 and 2 h, respectively. In the GPS data processing, four International GNSS Service (IGS) stations (INEG, NIST, NLIB, and PIE1) with a baseline length larger than 500 km are also used (see Fig. 2) to reduce the strong correlation of tropospheric parameters caused by the similar propagation paths of signals between satellites and stations in the local area (Rocken et al., 1995). The accurate zenith hydrostatic delay (ZHD) is calculated based on the Saastamoinen model (Saastamoinen, 1972) using the interpolated pressure parameters derived from the ECMWF ERA-Interim products with a resolution of . The zenith wet delay (ZWD) can be obtained by extracting ZHD from ZTD. Therefore, the SWDs of satellite rays with various azimuth and elevation angles are obtained using the wet mapping function (Niell et al., 2001). The weighted mean temperature, which is highly related to the specific area and season, can be obtained by statistical analyses of a large number of radiosonde profiles (Bevis et al., 1992). Here, Tm is calculated based on the empirical formula () proposed by Bevis et al. (1992) using the interpolated surface temperature (Ts) from ERA-Interim products. Therefore, the SWV can be obtained using the calculated conversion factor with Tm (Bevis et al., 1992).
3.2 Determination of the top boundary
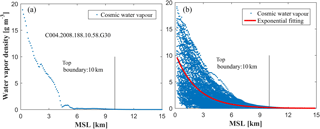
As described in previous studies, a reasonable top height of the tomographic body is important for tropospheric tomography (Yao and Zhao, 2016, 2017). If the height is too high, the estimated water vapour density values are possibly negative as more parameters near the altitude of the top boundary tend to zero. In contrast, a relatively large water vapour value is returned by the tomographic technique as some water vapour contents above the height of the top boundary are ignored. In our study, the top boundary of the research area is determined using the COSMIC RO product which is from the selected 178 “wetPrf” profiles from the period of 2006 to 2016. In addition, the water vapour density changes with altitude are also obtained from radiosonde recordings at station 72249 for the period from 2000 to 2015 to further verify the selected top boundary (Chen and Liu, 2014, 2016; Ye et al., 2016). Here, a principle is introduced to determine the final tomographic height. The principle is that the water vapour density is less than 0.2 g m−3 over the certain height, while the standard deviation (SD) is less than 0.05 g m−3, which has been used by Yao and Zhao (2016, 2017).
Figures 4 and 5 show the vertical distribution of water vapour density with height in a single event (left) and the water vapour distribution at different altitudes and exponential fitting curves for the selected period (right) derived from COSMIC RO and radio-sounding, respectively. It can be seen from Figs. 4 and 5 that the water vapour density generally decreases with the height increases, and the mean water vapour contents for the corresponding periods are both close to zero above a height of 10 km. The calculated water vapour density and SD for COSMIC RO and radiosonde aspects are 0.13/0.040 and 0.17/0.044 g m−3 at the height of 10 km, respectively, which both satisfy the principle mentioned above. Therefore, the top height of the tomographic body in our study was deemed to be 10 km.
In addition, a negative exponential function is introduced and the coefficients of the exponential model are estimated using the water vapour density from COSMIC “wetPrf” profiles as
where ρ represents the water vapour density while h refers to the geodetic height (unit of kilometres). This exponential model is used for establishing the vertical constraints between the adjacent layers as described in Sect. 2.1.
Based on the method proposed in Sect. 2, two schemes are designed to build the tomographic model and evaluate the performance of the various tomographic results. The two methods are presented as follows:
-
Method 1: only using the signals crossing out from the top side of the tomography area to reconstruct water vapour information based on the tomographic model (e.g. Eq. 3);
-
Method 2: both the signals penetrating from the top and side faces of a tomography body are used to reconstruct water vapour information based on the tomography model proposed in this paper (e.g. Eq. (5).
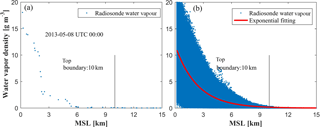
Figure 5The vertical distribution of water vapour density in a single sounding event (a) and the 3-D water vapour distribution of the tomography area and exponential fitting curve from 2000 to 2015 (b).
4.1 Utilisation rate of signals and number of voxels crossed by rays
If the satellite rays crossing the side faces of the tomography body are also used, the utilisation rate of signals and the number of voxels crossed by rays are expected to increase; therefore, the number of signals used and the number of voxels crossed by rays are first analysed using data from 13 stations derived from the CORS Network in Texas over a 15-day period. Figure 6 shows the number of signals used and the number of voxels crossed by rays, from which it can be seen that the number of signals used and the number of voxels crossed by rays of the proposed method are both larger than those from the conventional method. Table 1 lists statistical results pertaining to the number of signals used as well as the number of voxels crossed by rays for various conditions. The numerical result shows that the utilisation rate of satellite rays is increased by 21.06 %, while the number of voxels crossed by rays is improved by 1.53 %, from 81.39 % to 82.78 %, respectively.
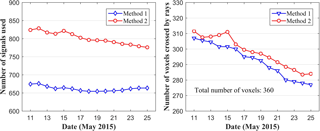
Figure 6The number of signals used and the number of voxels crossed by rays for the experimental period.
4.2 Water vapour comparison with radiosonde data
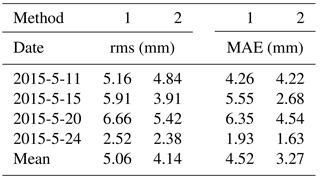
It has been proven that radiosonde data can provide fairly accurate vertical profiles of tropospheric water vapour; therefore, the water vapour profiles derived from radiosonde data are used as a reference to validate the tomographic results from various methods (Niell et al., 2001; Adeyemi and Joerg, 2012). The water vapour profiles for the location of radiosonde stations derived from various tomographic results are compared with that from radiosonde data at 00:00 and 12:00 UTC daily for the experimental period of 15 days. Here, rms and MAE are introduced to quantify the quality of the tomographic result. Figures 7 and 8 present the average rms and MAE comparisons of tomographic results derived from two methods with radiosonde data during the experimental period, respectively. The rms and MAE comparisons clearly show that the accuracy of water vapour profiles from method 2 is superior to that from method 1. Statistical results for the experimental period (Table 2) show that the mean rms∕MAE values of the proposed method are 1.49 and 1.04 g m−3, respectively, while the values using the conventional method are 1.74 and 1.24 g m−3, respectively.
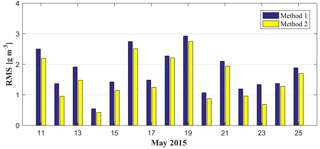
Figure 7The rms comparison of the tomographic result derived from two methods with radiosonde data during the experimental period.
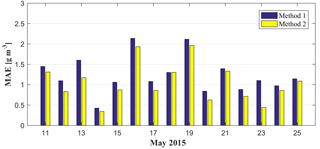
Figure 8The MAE comparison of the tomographic result derived from two methods with radiosonde data during the experimental period.
Table 2Statistical information on the tomographic result compared with radiosonde data for the experimental period.

In addition, water vapour profile comparisons for the specific two epochs at 00:00 UTC, 14 May and 12:00 UTC, 19 May are shown in Fig. 9. Those two times are selected because they correspond to the minimum and maximum rms values for the tested period. It can be seen from Fig. 9 that the water vapour density values derived from various tomographic methods match the radiosonde data at most altitudes. The statistical results show that the rms∕MAE values of method 2 are 0.43 and 2.75 g m−3, respectively, while the values of method 1 are 0.54 and 2.93 g m−3, respectively.
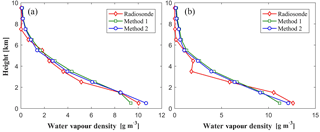
Figure 9Water vapour profile comparison derived from different tomographic methods and radiosondes at specific epochs, 14 May 00:00 UTC (a) and 19 May 12:00 UTC (b).
To investigate the relationship between water vapour profile error and altitude, a relative error is introduced and expressed as
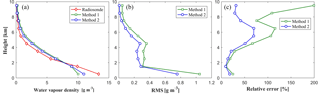
where xref is a reference value, which refers to the water vapour density derived from the radiosonde data, and xtomo is the reconstructed water vapour information based on different tomographic methods. For the selected period of 15 days, there are two epochs at 00:00 and 12:00 UTC daily. Therefore, a total of 30 sets of data are compared. Figure 10 presents the average water vapour profile comparison derived from different tomographic methods and radiosonde data (left), rms changes with altitude (middle) and relative error changes with altitude (right) for the experimental period. It can be seen that the average water vapour profiles at different altitudes derived from the proposed method better matched that from the radiosonde data, while the rms error and relative error of the proposed method are less than those arising from the use of the conventional method at all layers. Such results validate the superiority of the tomography method with an auxiliary area proposed in this paper. In addition, Fig. 10 shows that the rms error generally decreases with increasing altitude, while the relative error shows the opposite trend. This occurs because the water vapour is mainly concentrated in the lower layers and for the upper layers the water vapour density is very low; therefore, small differences between radiosonde and tomographic water vapour density values can lead to a large relative error.
4.3 SWV comparison
To validate the superiority of the proposed method, the data for 4 days are selected to compare the SWV values derived from the tomographic results and GAMIT 10.5. In this experiment, only 12 of 13 GPS stations in the research area participated in the reconstruction of the water vapour field, while the other station (TXSG) is regarded as a test station under the condition that other settings remained unchanged. The SWV values of the TXSG station calculated using the GPS observations are considered to be the true value. The comparison of SWV values derived from GPS-observed data and tomographic results of different methods is carried out with a tomography step of 0.5 h. Table 3 lists the average rms and MAE arising from the use of different tomographic methods and the statistical results for the selected 4-day period. It can be seen that the rms and MAE values of the proposed method (4.14 and 3.27 mm, respectively) are less than those of the traditional method (5.06 and 4.52 mm, respectively), which indicates the high accuracy of the proposed method.
An optimised tomographic method is proposed in conjunction with the concept of an auxiliary area for the inclusion of the signals crossing the side faces of the tomographic body. Both horizontal and vertical constraints are incorporated into the tomographic model. The top height of the tomography body is determined and the coefficients of the vertical constraint equation are fitted using the average water vapour density from the COSMIC “wetPrf” profiles for the period of 2006 to 2016. The proposed method improves the utilisation rate of signals used (21.06 %) as well as the number of voxels crossed by rays (1.53 %).
The proposed tomographic method is validated using the data of 13 GPS stations from the CORS Network in Texas over a 15-day period. The water vapour profile comparison with radiosonde data shows that the mean rms error and MAE of the proposed method are decreased by 14.37 % and 16.13 %, respectively, when compared to the traditional method. The water vapour profile error changes with altitude also show that the rms and relative errors of the proposed method are less than that from the conventional method at different heights, which indicates the superiority of the proposed method. The SWV comparison between the GAMIT-estimated and tomographic-derived values shows that the rms error and MAE of the proposed method have been improved by 18.18 % and 27.62 %, respectively, when compared to the conventional method, which further confirms its superiority.
In this paper, we used (1) GNSS observations and corresponding meteorological data, which can be downloaded from the Surveying and Mapping Office/Land Department (2018), Hong Kong (https://www.geodetic.gov.hk/smo/index.htm); (2) radiosonde data, which can be downloaded from the IGRA center (ftp://ftp.ncdc.noaa.gov/) (NOAA, 2018); and (3) COSMIC RO “wetPrf” profiles, which can be downloaded from UCAR (2018) (http://www.cosmic.ucar.edu/).
QZ mainly contributed to this work. YY and WY conducted the analysis of the approach proposed, and they contributed to the corrections and structure of this paper. PX contributed to the analysis of the COSMIC RO products. All the authors participated in the writing and all commented on the paper.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Advanced Global Navigation Satellite Systems tropospheric products for monitoring severe weather events and climate (GNSS4SWEC) (AMT/ACP/ANGEO inter-journal SI)”. It is not associated with a conference.
The authors would like to thank the International GNSS Service (IGS) and
National Geodetic Survey (NGS) for providing the GPS observations and the
post-mission satellite precise products. The IGRA and ECMWF are also thanked
for providing the corresponding meteorological parameters. The University
Corporation for Atmospheric Research (UCAR) is thanked for providing the
COSMIC RO products. This research was supported by the Key Laboratory of
Geospace Environment and Geodesy, Ministry of Education, Wuhan University
(17-01-02).
The topical editor, Petr
Pisoft, thanks Chris Sioris, Kefei Zhang, and three anonymous referees for
help in evaluating this paper.
Adeyemi, B. and Joerg, S.: Analysis of water vapour over Nigeria using radiosonde and satellite data, J. Appl. Meteorol. Clim., 51, 1855–1866, 2012.
Bender, M., Stosius, R., Zus, F., Dick, G., Wickert, J., and Raabe, A.: GNSS water vapour tomography–Expected improvements by combining GPS, GLONASS and Galileo observations. Adv. Space Res., 47, 886–897, 2011a.
Bender, M., Dick, G., Ge, M., Deng, Z., Wickert, J., Kahle, H. G., and Tetzlaff, G. Development of a GNSS water vapour tomography system using algebraic reconstruction techniques, Adv. Space Res., 47, 1704–1720, 2011b.
Benevides, P., Catalão, J., and Miranda, P. M.: Experimental GNSS tomography study in Lisbon (Portugal), Física de la Tierra, 26, 65–79, 2014.
Bevis, M., Businger, S., Herring, T. A., Rocken, C., Anthes, R. A., and Ware, R. H.: GPS meteorology: Remote sensing of atmospheric water vapor using the Global Positioning System, J. Geophys. Res.-Atmos., 97, 15787–15801, 1992.
Bi, Y., Mao, J., and Li, C.: Preliminary results of 4-D water vapour tomography in the troposphere using GPS, Adv. Atmos. Sci., 23, 551–560, 2006.
Bourjot, L. and Romanowicz, B.: Crust and upper mantle tomography in Tibet using surface waves, Geophys. Res. Lett., 19, 881–884, 1992.
Bramlet, R.: Reconstruction Tomography in Diagnostic Radiology and Nuclear Medicine, Clin. Nucl. Med., 3, 245, 1978.
Hudnut, K., Röcken, C., Sleziak, M., Syndergaard, S., Hunt, D., Schreiner, B., Sokolovskiy, S., and Wee, T.-K.: CDAAC: Algorithms for inverting Radio Occultation signals in the neutral atmosphere, COSMIC Project Office, University Corporation for Atmospheric Research, available at: http://cosmic-io.cosmic.ucar.edu/cdaac/doc index.html, 2007.
Champollion, C., Masson, F., Bouin, M. N., Walpersdorf, A., Doerflinger, E., Bock, O., and Van Baelen, J.: GPS water vapour tomography: preliminary results from the ESCOMPTE field experiment, Atmos. Res., 74, 253–274, 2005.
Chen, B. and Liu, Z.: Voxel-optimized regional water vapour tomography and comparison with radiosonde and numerical weather model. J. Geodesy, 88, 691–703, 2014.
Chen, B. and Liu, Z.: Assessing the performance of troposphere tomographic modeling using multi-source water vapor data during Hong Kong's rainy season from May to October 2013, Atmos. Meas. Tech., 9, 5249–5263, https://doi.org/10.5194/amt-9-5249-2016, 2016.
de Haan, S., Holleman, I., and Holtslag, A. A.: Real-time water vapour maps from a GPS surface network: Construction, validation, and applications, J. Appl. Meteorol. Clim., 48, 1302–1316, 2009.
Ding, N., Zhang, S. B., Wu, S. Q., Wang, X. M., and Zhang, K. F.: Adaptive node parameterization for dynamic determination of boundaries and nodes of GNSS tomographic models, J. Geophys. Res.-Atmos., 123, 1990–2003, 2018.
Duan, J., Bevis, M., Fang, P., Bock, Y., Chiswell, S., Businger, S., and McClusky, S.: GPS meteorology: Direct estimation of the absolute value of precipitable water, J. Appl. Meteorol., 35, 830–838, 1996.
Emardson, T. R., Johansson, J., and Elgered, G.: The systematic behavior of water vapour estimates using four years of GPS observations. IEEE T. Geosci. Remote, 38, 324–329, 2000.
Flores, A., Ruffini, G., and Rius, A.: 4D tropospheric tomography using GPS slant wet delays, Ann. Geophys., 18, 223–234, 2000.
Gao, J., Xue, M., Shapiro, A., and Droegemeier, K. K.: A variational method for the analysis of three-dimensional wind fields from two Doppler radars, Mon. Weather Rev., 127, 2128–2142, 1999.
Gendt, G., Dick, G., Reigber, C., Tomassini, M., Liu, Y., and Ramatschi, M.: Near real time GPS water vapour monitoring for numerical weather prediction in Germany, J. Meteorol. Soc. Jpn, 82, 361–370, 2004.
Hajj, G. A., Ibanez–Meier, R., Kursinski, E. R., and Romans, L. J.: Imaging the ionosphere with the Global Positioning System, Int. J. Imag. Syst. Tech., 5, 174–187, 1994.
Herring, T. A., King, R. W., and McClusky, S. C.: GAMIT reference manual, GPS Analysis at MIT, release, 10.4, 36, available at: http://www-gpsg.mit.edu/~simon/gtgk/index.htm (last access: 20 September 2014), 2010.
Hirahara, K.: Local GPS tropospheric tomography, Earth Planets Space, 52, 935–939, 2000.
Kissling, E., Ellsworth, W. L., Eberhart-Phillips, D., and Kradolfer, U.: Initial reference models in local earthquake tomography, J. Geophys. Res.-Ea., 99, 19635–19646, 1994.
Lee, S. W., Kouba, J., Schutz, B., Kim, D. H., and Lee, Y. J.: Monitoring precipitable water vapour in real-time using global navigation satellite systems, J. Geodesy, 87, 923–934, 2013.
Niell, A. E., Coster, A. J., Solheim, F. S., Mendes, V. B., Toor, P. C., Langley, R. B., and Upham, C. A.: Comparison of measurements of atmospheric wet delay by radiosonde, water vapour radiometer, GPS, and VLBI, J. Atmos. Ocean. Tech., 18, 830–850, 2001.
NOAA: Radiosonde data, available at: ftp://ftp.ncdc.noaa.gov/, last access: 27 July 2018.
Notarpietro, R., Cucca, M., Gabella, M., Venuti, G., and Perona, G.: Tomographic reconstruction of wet and total refractivity fields from GNSS receiver networks, Adv. Space Res., 47, 898–912, 2011.
Park, S. K.: Nonlinearity and predictability of convective rainfall associated with water vapor perturbations in a numerically simulated storm. J. Geophys. Res.-Atmos., 104, 31575–31587, 1999.
Raja, M. R. V., Gutman, S. I., Yoe, J. G., McMillin, L. M., and Zhao, J.: The validation of AIRS retrievals of integrated precipitable water vapour using measurements from a network of ground-based GPS receivers over the contiguous United States, J. Atmos. Ocean. Tech., 25, 416–428, 2008.
Ran, B. Y. and Ge, W. Z.: Singular value decomposition method compared with damping least square method, Geophys. Comput. Technol., 1, 46–49, 1997.
Rius, A., Ruffini, G., and Cucurull, L.: Improving the vertical resolution of ionospheric tomography with GPS occultations, Geophys. Res. Lett., 24, 2291–2294, 1997.
Rocken, C., Ware, R., Van Hove, T., Solheim, F., Alber, C., Johnson, J., and Businger, S.: Sensing atmospheric water vapour with the Global Positioning System, Geophys. Res. Lett., 20, 2631–2634, 1993.
Rocken, C., Hove, T. V., Johnson, J., Solheim, F., Ware, R., Bevis, M., and Businger, S.: GPS/STORM-GPS sensing of atmospheric water vapour for meteorology, J. Atmos. Ocean. Tech., 12, 468–478, 1995.
Rohm, W. and Bosy, J.: Local tomography troposphere model over mountains area, Atmos. Res., 93, 777–783, 2009.
Rohm, W. and Bosy, J.: The verification of GNSS tropospheric tomography model in a mountainous area, Adv. Space Res., 47, 1721–1730, 2011.
Rohm, W., Zhang, K., and Bosy, J.: Limited constraint, robust Kalman filtering for GNSS troposphere tomography, Atmos. Meas. Tech., 7, 1475–1486, https://doi.org/10.5194/amt-7-1475-2014, 2014.
Saastamoinen, J.: Atmospheric correction for the troposphere and stratosphere in radio ranging satellites, The use of artificial satellites for geodesy, 15, 247–251, 1972.
Skone, S. and Hoyle, V.: Troposphere modeling in a regional GPS network, J. Glob. Position., 4, 230–239, 2005.
Smith, T. L., Benjamin, S. G., Gutman, S. I., and Sahm, S.: Short-range forecast impact from assimilation of GPS-IPW observations into the Rapid Update Cycle, Mon. Weather Rev., 135, 2914–2930, 2007.
Surveying and Mapping Office/Land Department: GNSS observations and corresponding meteorological data, available at: https://www.geodetic.gov.hk/smo/index.htm, last access: 27 July 2018.
Troller, M., Geiger, A., Brockmann, E., Bettems, J. M., Bürki, B., and Kahle, H. G.: Tomographic determination of the spatial distribution of water vapour using GPS observations, Adv. Space Res., 37, 2211–2217.3, 2006.
UCAR: COSMIC RO “Wetprf” profiles, available at: http://www.cosmic.ucar.edu/, last access: 27 July 2018.
Wan, R.: Research progress of the unconventional observing technology and the data used in the study of rainstorm in China, Adv. Meteorol. Sci. Technol., 4, 24–35, 2014.
Ye, S., Xia, P., and Cai, C.: Optimization of GPS water vapor tomography technique with radiosonde and COSMIC historical data, Ann. Geophys., 34, 789–799, https://doi.org/10.5194/angeo-34-789-2016, 2016.
Yao, Y. and Zhao, Q.: A novel, optimized approach of voxel division for water vapor tomography, Meteorol. Atmos. Phys., 129, 1–14, 2016.
Yao, Y. and Zhao, Q.: Maximally Using GPS Observation for Water Vapor Tomography, IEEE T. Geosci. Remote, 54, 7185–7196, 2017.
Yao, Y. B., Zhao, Q. Z., and Zhang, B.: A method to improve the utilization of GNSS observation for water vapor tomography, Ann. Geophys., 34, 143–152, https://doi.org/10.5194/angeo-34-143-2016, 2016.
Zhang, K., Manning, T., Wu, S., Rohm, W., Silcock, S., and Choy, S.: Capturing the Signature of Severe Weather Events in Australia Using GPS Measurements, IEEE JSTARS, 8, 1839–1847, 2015.
Zhao, Q. and Yao, Y.: An improved troposphere tomographic approach considering the signals coming from the side face of the tomographic area, Ann. Geophys., 35, 87–95, https://doi.org/10.5194/angeo-35-87-2017, 2017.